Лекція 3. Електричнi кола постiйного струму

3.4. Метод вузлових потенціалів

Метод вузлових потенціалів (вузлових напруг) заснований на законі струмів Кірхгофа та законі Ома. Цей метод дозволяє зменшити кількість рівнянь в системі до (n_в-1).

Алгоритм реалізації методу вузлових потенціалів можна подати у вигляді:

1. Довільно вибираємо напрямки струмів у вітках.
2. Заземлюємо один з вузлів, завдяки чому його потенціал стає рівним нулю. Цей вузол зазвичай називають базисним вузлом.
3. Складаємо систему лінійних незалежних рівнянь для вузлів електричного кола за законом струмів Кірхгофа. Розв’язання цієї системи рівнянь дозволяє знайти потенціалі вузлів, а в подальшому й напруги (різниці потенціалів) між вказаними вузлами.
4. Використовуючи закон Ома для ділянки кола, знаходимо струми у вітках заданого кола.

Розглянемо використання методу вузлових потенціалів для розрахунку кола, аналогічного тому, яке використовувалося під час розгляду методу контурних струмів. Для зручності це коло наведене на рис. 3.14 з позначками, необхідними для реалізації алгоритму методу вузлових потенціалів.

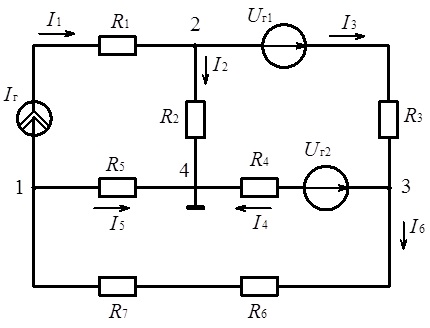
Рис. 3.14. Схема до ілюстрації методу вузлових потенціалів

 

Напрямки струмів у вітках вибираємо довільно.

Заземлюємо вузол 4, тим самим роблячи його базисним. Це означатиме, що потенціал цього вузла дорівнюватиме нулю (V₄=0).

Для вузлів 1, 2, 3 складаємо систему лінійних незалежних рівнянь за законом струмів Кірхгофа, тобто враховуючи, що алгебраїчна сума струмів у кожному вузлі має дорівнювати нулю.

За вказаних умов у вузлі 1 зійдуться струми:

• вузловий струм, який утворюється джерелом напруги або струму (в даному випадку це струм - І_г, який витікає з вузла 1);
• власний струм вузла, який визначається потенціалом першого вузла та провідностями всіх віток, що у цьому вузлі сходяться, а саме

;

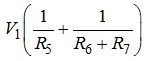• взаємні струми вузла, які визначаються потенціалами суміжних вузлів та провідностями відповідних віток, що зв’язують ці вузли з вибраним (вузлом 1), а саме:

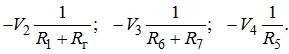
Нагадаємо, що внутрішній опір джерела струму R_г спрямовується до нескінченності, тому провідність відповідної вітки дорівнює нулю; дорівнює нулю й потенціал V₄ вузла 4. Тобто серед взаємних струмів вузла 1 ненульовим виявляється лише струм, що зв’язує перший і вузол. Зазначимо, що взаємні струми вузла завжди беруться зі знаком «мінус», а знак вузлового струму залежить від того, втікає цей струм у вузол чи витікає з нього. Вузловий струм, який утворюється джерелом напруги (див., наприклад, вузол 2), визначається відношенням напруги цього джерела до опору вітки, в яку це джерело увімкнене. Проводячи для вузлів 2 та 3 аналогічні міркування, отримуємо систему рівнянь вузлових потенціалів для заданої схеми, а саме:

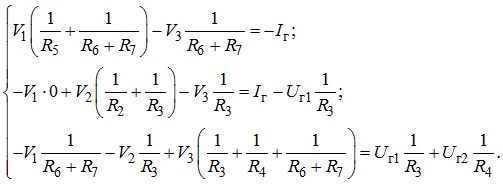
В канонічній формі запису наведена система рівнянь матиме вигляд:

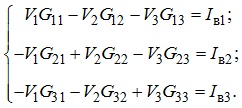
В останній системі рівнянь використані позначення:

• потенціали вузлів 1, 2, 3 електричного кола:

;

• власні провідності:

вузла 1 (G₁₁),

вузла 2 (G₂₂),

вузла 3 (G₃₃),

які дорівнюють сумі провідностей всіх віток, що приєднані до кожного вказаного вузла, визначаються як:

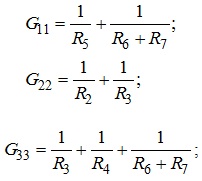
• взаємні провідності:

вузла 1 та вузла 2 (G₁₂ = G₂₁),

вузла 1 та вузла 3 (G₁₃ = G₃₁),

вузла та вузла 3 (G₂₃ = G₃₂),

які дорівнюють сумі провідностей всіх віток, що включені між відповідною парою вузлів, визначаються як:

;

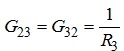• задавальні вузлові струми

вузлів 1 (І_з1),

вузла 2 (І_з2),

вузла 3 (І_з3),

які дорівнюють алгебраїчній сумі струмів всіх джерел, підключених до кожного з вузлів, визначаються як:

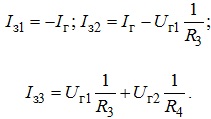
Під час складання рівнянь вузлових потенціалів необхідно користуватися наступним «правилом знаків»:

• власні провідності завжди беруться зі знаком «плюс»,
• взаємні провідності завжди беруться зі знаком «мінус»,
• задавальні струми джерел беруться зі знаком «плюс», якщо ці струми направлені до вузла, і зі знаком «мінус», якщо ці струми направлені від вузла.

За умови, що резистивне електричне коло містить п вузлів, отримуємо узагальнену систему рівнянь в канонічній формі. За умови, що заземлено п-й вузол, тобто (Vп=0), матимемо:

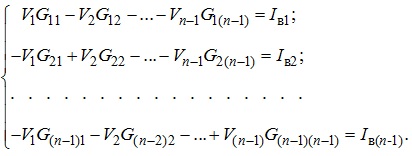   (3.11)

З системи лінійних рівнянь (3.11) знаходимо потенціали вузлів:

,

використовуючи, наприклад, правило Крамера.

Для прикладу, що розглядався вище, зі сформованої системи рівнянь для кола, наведеного на рис. 3.14, за правилом Крамера потенціали вузлів 1, 2 та 3 знаходимо як:

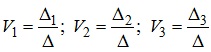
де Δ - головний визначник системи, який розраховується як:

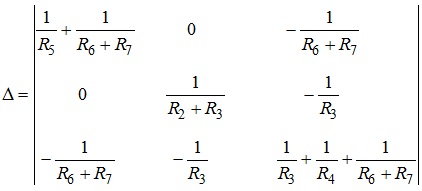
Визначники Δ₁, Δ₂, Δ₃ отримуємо, замінюючи в головному визначнику відповідний стовпець на стовпець задавальних вузлових струмів. Надалі, знаючи потенціали вузлів, знаходимо струми у вітках кола, використовуючи закон Ома. Маємо:

.

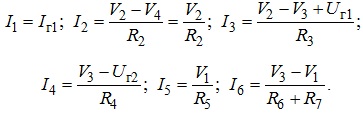Під час використання методу вузлових потенціалів слід пам’ятати, що за наявності у колі вітки, яка містить виключно ідеальне джерело напруги, як базисний вибирають один з вузлів, до яких приєднана ця вітка. При цьому потенціал другого вузла виявляється одразу відомим, адже він дорівнюватиме напрузі вказаного джерела взятому зі знаком «плюс» або «мінус» в залежності від полярності цього джерела. Рівняння за методом вузлових потенціалів для такого вузла складати не треба, але його потенціал враховується при складанні рівнянь для інших вузлів.

Струм у вітці з ідеальним джерелом напруги не можна розраховувати, використовуючи закон Ома, адже опір такого джерела дорівнює нулю. Тому для розрахунку струмів у таких вітках використовують закон струмів Кірхгофа після розрахунку струмів у всіх інших вітках електричного кола.