Лекція 4. Електричні кола однофазного синусоїдного струму

1. Основні визначення та форми відображення синусоїдних величин

Як вже було зазначено, існування електричного струму нерозривно пов’язане з існуванням електричного і магнітного полів. При змінному струмі ці поля змінюються у часі. Магнітне поле, що змінюється у часі, наводить у провідниках ЕРС. Електричне поле, що змінюється у часі супроводжується зміненням величини заряду, наведеного цим полем на провідниках. У провідниках, а частково і в оточуючому середовищі електромагнітна енергія перетворюється на теплову. Деяка частка енергії електромагнітного поля випромінюється. Описані явища відбуваються на всіх ділянках електричного кола, яким протікає змінний електричний струм.

На практиці для спрощення аналізу реальне електричне коло змінного струму замінюють еквівалентною схемою заміщення, елементи якої ідеалізовані. Це дозволяє розподілити вказані процеси між елементами електричного кола змінного струму, суттєво спростивши задачі дослідження й розрахунку таких кіл. Електричні величини (струми, напруги, ЕРС), які змінюються в часі за величиною та напрямком називаються змінними величинами. Один з можливих напрямків змінної електричної величини приймають як додатний напрямок.

Електрична величина вважається цілком визначеною за умови, що відома її залежність від часу, тобто відома відповідна функція f(t) та вказано додатний напрямок цієї величини.

Значення, які набувають змінні електричні величини кожної миті часу, називаються миттєвими значеннями. Для позначення миттєвих значень струмів, напруг та ЕРС зазвичай вживають малі літери латинського алфавіту, наприклад, i, u, e. Величини, миттєві значення яких повторюються через визначені однакові проміжки часу, називають періодичними, а найменший проміжок часу, через які ці повторення відбуваються, називають періодом, який зазвичай позначають як Т. Таким чином, наприклад, миттєве значення періодичного струму в кожному циклі повторення дорівнюватиме:

.

Величина, обернена періоду відповідної змінної величини, називається циклічною частотою f цієї величини (зазвичай слово «циклічна» опускають). Отже:

.

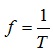Циклічна частота вимірюється в герцах (Гц).

При частоті 1 Гц період Т=1 с, тобто 1 Гц = 1 с^-1.

Приклад періодичного струму наведений на рис. 4.1. Зазначимо, що постійний струм можна розглядати, як такий окремий випадок періодичного струму, для якого період Т є нескінченно великим. При цьому, звичайно, циклічна частота дорівнюватиме нулю, тобто:

 

Крім циклічної частоти поширення отримала величина ω, що визначається як:

.

Ця величина зветься кутовою або круговою частотою і вимірюється в рад/с. Зміст цієї величини обговорюватимемо надалі.

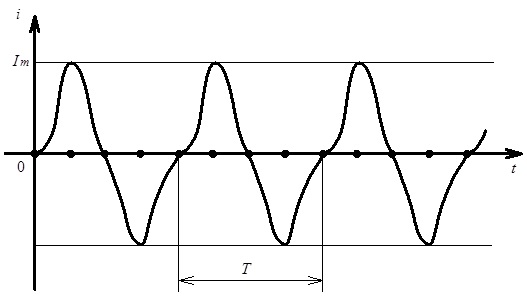
Рис. 4.1. Приклад періодичного струму Т - період; І_т - амплітудне значення

 

Найбільше з миттєвих значень електричних величин, що періодично змінюються, зветься максимальним або амплітудним значенням (амплітудою). Найбільш поширені найпростіші гармонічні або синусоїдні електричні величини (струми, напруги, ЕРС). За умови, що електричне коло лінійне, при синусоїдній ЕРС струми та напруги також синусоїдні. В енергетичних системах більшості країн світу (в т.ч. в країнах бувшого СРСР та Європи прийнята стандартна частота синусоїдного струму 50 Гц. В США – 60 Гц. Взагалі кажучи на сьогодні в різних за призначенням системах знаходять застосування електричні коливання від долів герца до мільярдів герц. Аналітичний запис синусоїдної величини (наприклад, ЕРС) легко отримати з загального визначення синусоїдної функції, а саме:

.

Графічне зображення синусоїдної ЕРС наведене на рис. 4.2.

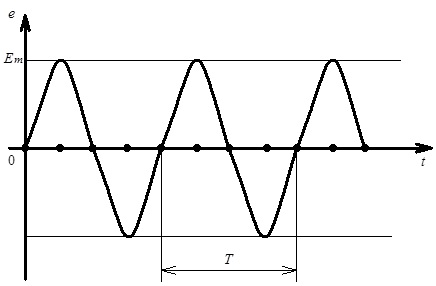
Рис. 4.2. Графічне зображення синусоїдної ЕРС

 

Найзручнішим виявилося зображення синусоїдної електричної величини деяким вектором, який обертається з постійною швидкістю ω та характеризується довжиною, що дорівнює амплітудному значенню цієї величини. При цьому миттєві значення відповідної величини відображаються проекціями цього вектора на вісь ординат (див. рис. 4.3, де у векторному вигляді відображена ЕРС).

Припустимо, що при t=0 (тобто в момент початку відліку часу) положення вектора відповідає співвідношенню:

,

де ψ₁ - електричний кут, що визначає початкове значення ЕРС.

 

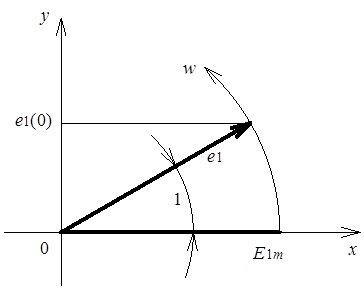
Рис. 4.3. Векторне відображення синусоїдної ЕРС (прийняті позначення: )

 

При подальшому обертанні вектора е₁ його поточне положення визначатиметься співвідношенням:

.

Кут ψ₁, яким визначається початкове значення синусоїдної ЕРС (або іншої електричної величини – струму, напруги) зветься початковим фазним кутом або початковою фазою.

Припустимо, що в електричному колі діє ще одна ЕРС, початкове значення якої визначається як:

,

а поточне

Зазначимо, що частоти ЕРС Е₁, Е₂ однакові. Різниця початкових фаз цих двох ЕРС (в загальному випадку двох будь-яких синусоїдних електричних величин) зветься кутом зсуву фаз (часто, зсувом фаз) і визначається як:

.

Куту зсуву фаз двох синусоїдних величин відповідає час:

.

Час t₁₂ показує на яку частку періоду (тобто на який відрізок часу) одна синусоїдна величина досягає своїх нульових (або амплітудних) значень раніше (пізніше) за другу. При цьому одна з двох електричних величин, що розглядаються, зветься випереджаючою за фазою, а друга – відстаючою.  Про величини, для яких ψ₁₂=0, говорять, що вони співпадають за фазою. Отже кут поточної фази синусоїдної величини з часом безперервно зростає, збільшуючись протягом періоду Т на величину 2p. Величина:

.

показує швидкість, з якою змінюється кут поточної фази. Як вже було визначено ця величина зветься кутовою частотою на відміну від циклічної частоти f. Вимірюється кутова частота числом радіанів, на яке поточна фаза збільшується протягом секунди.

Наприклад, для частоти f=50 Гц кутова частота дорівнюватиме:

.

Для співставлення синусоїдних величин їх зручно (зазвичай так і роблять) відображати у графічному або векторному вигляді на одному рисунку. Сукупність декількох синусоїд, що відображають синусоїдні величини, зветься хвильовою діаграмою. В загальному випадку частоти зображених на хвильовій діаграмі величин можуть бути різними. На рис. 4.4 наведена хвильова діаграма двох синусоїдних величин однакової частоти, але з різними початковими фазами, а саме:

.

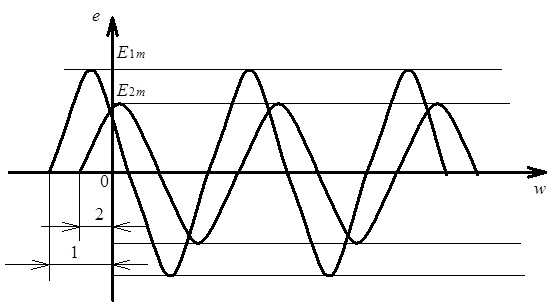
Рис. 4.4. Хвильова діаграма двох синусоїдних ЕРС однакової частоти й з різними початковими фазами ()

 

Сукупність декількох векторів, що відображають відповідні синусоїдні величини, зветься векторною діаграмою. При цьому частоти таких величин мають бути однаковими, щоб між векторами, які обертаються, зберігався постійний зсув фаз. На рис. 4.5 наведена векторна діаграма двох синусоїдних величин:

.

Зазначимо, що довжини вказаних векторів е₁, е₂ відповідно дорівнюють Е_1т, Е_2т і, звичайно, залишаються незмінними в процесі обертання цих векторів навколо початку координат (з кутовою швидкістю w).

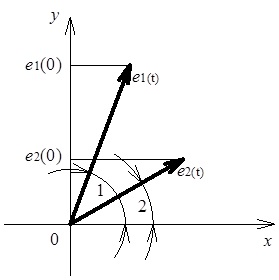
Рис. 4.5. Векторна діаграма двох синусоїдних ЕРС однакової частоти й з різними початковими фазами ()

 

Під час розрахунку електричних кіл синусоїдного струму доводиться додавати та віднімати значення синусоїдних струмів, напруги, ЕРС та ін. При цьому в кожен момент часу миттєві значення сумарної величини дорівнює алгебраїчній сумі миттєвих значень доданків.

Зважаючи на те, що миттєві значення синусоїдних величин відображаються проекціями векторів, які обертаються, вказані математичні операції над миттєвими значеннями електричних величин можна виконати як операції над відповідними векторами (див. рис. 4.6).

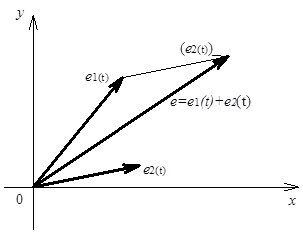
Рис. 4.6. Ілюстрація додавання миттєвих значень двох ЕРС