Тема 3. Концептуальніо-наукові засади математичного моделювання бізнес=проєктів

4. Класифікація економіко-математичних моделей

Для класифікації економіко-математичних моделей використовують різні класифікаційні ознаки.

За цільовим призначенням економіко-математичні моделі поділяються на теоретико-аналітичні, що використовуються під час дослідження загальних властивостей і закономірностей економічних процесів, і прикладні, що застосовуються у розв’язанні конкретних економічних задач (моделі економічного аналізу, прогнозування, управління).

Відповідно до загальної класифікації математичних моделей вони поділяються на функціональні та структурні, а також проміжні форми (структурно-функціональні). Типовими структурними моделями є моделі міжгалузевих зв’язків. Прикладом функціональної моделі може слугувати модель поведінки споживачів в умовах товарно-грошових відносин.

Моделі поділяють на дескриптивні та нормативні. Прикладом дескриптивних моделей є виробничі функції та функції купівельного попиту, побудовані на підставі опрацювання статистичних даних. Типовим прикладом нормативних моделей є моделі оптимального (раціонального) планування, що формалізують у той чи інший спосіб цілі економічного розвитку, можливості і засоби їх досягнення.

За характером відображення причинно-наслідкових аспектів розрізняють моделі жорстко детерміновані і моделі, що враховують випадковість і невизначеність.

За способами відображення чинника часу економіко-математичні моделі поділяються на статичні й динамічні.

Моделі економічних процесів надзвичайно різноманітні за формою математичних залежностей. Важливо виокремити клас лінійних моделей, що набули значного поширення завдяки зручності їх використання. Відмінності між лінійними і нелінійними моделями є суттєвими не лише з математичного погляду, а й у теоретико-економічному плані, адже багато залежностей в економіці мають принципово нелінійний характер.

За співвідношенням екзогенних і ендогенних змінних, які включаються в модель, вони поділяються на відкриті і закриті. Повністю відкритих моделей не існує; модель повинна містити хоча б одну ендогенну змінну. Повністю закриті економіко-математичні моделі, тобто такі, що не містять екзогенних змінних, надзвичайно рідкісні. Переважна більшість економіко-математичних моделей посідає проміжну позицію і розрізняється за ступенем відкритості (закритості).

Класифікація видів математичних моделей може проводитися й за такими ознаками: аналітичне та комп’ютерне моделювання (рис.3.4).

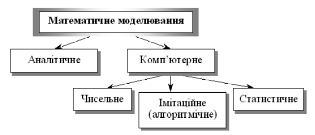
Рис 3.4. Аналітичне та комп’ютерне моделювання

Для аналітичного моделювання характерним є те, що процеси функціонування елементів системи записують у вигляді деяких математичних співвідношень (алгебраїчних, інтегро-диференційних, кінцево-різницевих тощо) чи логічних умов.

Комп’ютерне моделювання характеризується тим, що математична модель системи (використовуючи основні співвідношення аналітичного моделювання) подається у вигляді деякого алгоритму та програми, придатної для її реалізації на комп’ютері, що дає змогу проводити з нею обчислювальні експерименти. Залежно від математичного інструментарію (апарату), що використовується в побудові моделі, та способу організації обчислювальних експериментів можна виокремити три взаємопов’язані види моделювання: чисельне, алгоритмічне (імітаційне) та статистичне.

У чисельному моделюванні для побудови комп’ютерної моделі використовуються методи обчислювальної математики, а обчислювальний експеримент полягає в чисельному розв’язанні деяких математичних рівнянь за заданих значень параметрів і початкових умов.

Алгоритмічне (імітаційне) моделювання (може бути детермінованим та стохастичним) — це вид комп’ютерного моделювання, для якого характерним є відтворення на комп’ютері (імітація) процесу функціонування досліджуваної складної системи.

Статистичне моделювання — це вид комп’ютерного моделювання, який дозволяє отримати статистичні дані відносно процесів у модельованій системі.