Тема 5. Принципи розрахунку, покладені в основу обчислювальних комплексів
3. Компонування фізичних рівнянь
Фізичні рівняння:
D {S} = {e}. (6.25)
Розрахункова стержнева схема складається із вузлів, які
з'єднані між собою лінійними СЕ, що
називаються стержнями. У лінійно-деформованих
об'єктах між вузловими
реакціями і вузловими
переміщеннями, що їх зумовлюють, існує лінійна залежність (6.20)R = K D
, де K – матриця жорсткості (матриця пружності), що визначає лінійний зв'язок між векторами напружень s та векторами деформацій , s = k e (закон Гука),де k – це вузлова
реакція, що викликана
вузловим переміщенням умови
що всі інші переміщення дорівнюють нулю. Розглянемо навантажений стержень
i-j рис. 6.5. Рисунок 6.5 – До побудови
матриці піддатливості для стержневого СЕ Для знаходження Kij потрібно почергово надавати одиничні переміщення вузлам дискретної моделі і знаходити
сили, які при цьому передаватимуться на вузли. Матриця
жорсткості K є оберненою до матриці піддатливості D . Деформацію стержня {e} характеризує три компоненти:φ,φ,l, які можна визначити Переміщення δij можна знайти за відомими формулами Максвелла Мора Систему (2.26)
можна подати в матричному вигляді: Коли знехтувати поздовжніми деформаціями l Якщо стержнів в системі "n"
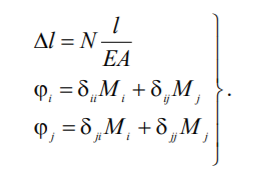 (6.26)
(6.26) (6.27)
(6.27)
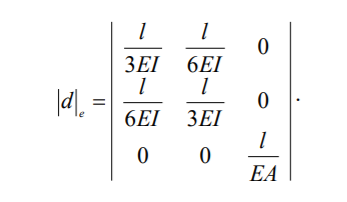 (6.29)
(6.29) (6.30)
(6.30) (6.31)
(6.31)
Шрифти
Розмір шрифта
Колір тексту
Колір тла
Кернінг шрифтів
Видимість картинок
Інтервал між літерами
Висота рядка
Виділити посилання
Вирівнювання тексту
Ширина абзацу