Тема 5. Раціональне розбиття на скінченні елементи
5. Сполучення різних типів скінченних елементів.
Лише у окремих випадках вся конструкція представлена елементами одинакового типу (наприклад, лише елементами плити); частіше зустрічаються випадки, коли в одній розрахунковій моделі присутні і стержневі, і оболонкові, і інші елементи.
Сучасні розрахункові програмні комплекси допускають майже довільну комбінацію скінченних елементів найрізноманітніших типів, розмірності, розмірів і геометричної форми, а також з різними чисельними характеристиками жорсткості, проте при їх використанні необхідно враховувати особливості сполучення різних типів скінченних елементів.
Сполучення колон і плит
За останні роки популярними стали розрахунки стержневих каркасів будівель і споруд спільно з плитними фундаментними конструкціями.
Розглянемо дискретну розрахункову схему, що поєднує в собі скінченні елементи плити і стержневі елементи, жорстко приєднані до плити. Сітка скінченних елементів плити вибирається так, щоб стержні каркаса будівлі потрапляли у вузли сіткового розбиття плити. Якщо не робити жодних додаткових заходів, то описана вище розрахункова схема у вузлах стиковки плитних і стержневих елементів забезпечить спільність як вертикальних переміщень плити і каркасу (переміщень в напрямі, перпендикулярному площині плити), так і відповідних кутів повороту. Проте, отримувані в цій розрахунковій схемі згинні моменти в перетинах стійок, що примикають до плити, не мають відношення до дійсного розподілу внутрішніх зусиль.
Починаючи з деякої сіткової розбивки, подальше дроблення сітки повинне призводити до зменшення абсолютних значень згинних моментів в стержнях в місцях їх закладення в плиту. У границі, при прямуванні максимального розміру сіткового елемента до нуля ці згинні моменти також повинні прямувати до нуля, а це означає, що дана розрахункова схема забезпечує не жорстке, а шарнірне приєднання елементів каркаса до плити. Те, що користувач формально при вибраній їм сітці набуває деяких відмінних від нуля чисельних значень згинних моментів свідчить лише про погрішність дискретизации в методі скінченних елементів.
Для того, щоб відкоректувати розрахункову схему, слід розглянути конструктивне рішення в місці прикріплення каркаса до плити. Якщо стійки каркаса приєднані до плити за допомогою підколонників, то останні можуть розглядатися як абсолютно жорстке тіло, що не міняє своїх розмірів при будь-яких змінах сітки скінченних елементів плити. Розміри ж абсолютно жорсткого тіла можна призначити, виходячи з розмірів підколонника (а х b) з врахуванням розподілу тиску від нього на плиту під кутом 45° (рис. 5.5) до серединної поверхні плити, що повністю відповідає традиційній інженерній практиці.
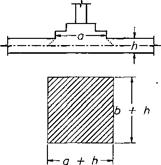 Рисунок 5 .5 – Сполучення колони з плитою через підколонник
Рисунок 5 .5 – Сполучення колони з плитою через підколонник
У цій схемі зосереджений момент від стійок каркаса передається на плиту через жорстку шайбу, розміри якій а+h і b+h не зв’язані з розмірами сітки скінченних елементів, а значить, і з погрішністю дискретизації. Хоча погрішність дискретизації і впливатиме на чисельні значення згинних моментів в стійках, вона не надасть такої катастрофічної дії на відхилення розрахункової схеми від реальної конструкції, як це було у вихідній постановці завдання без введення в розрахункову схему жорсткого тіла. У тому випадку, коли підколонники відсутні, можна в якості розмірів жорсткого тіла прийняти розміри поперечного перетину стійки.
Опирання плити на точкову опору
Такого типу проблема виникає в завданні опирання плити на одиночну колону при необхідності сприйняття крутних моментів відносно вертикальної осі колони. В цьому випадку можна рекомендувати введення абсолютно жорстких вставок (рис. 5.6).
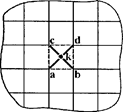
Рисунок 5.6 – Введення абсолютно жорстких вставок при обпиранні
плити на колону
Таке рішення з одного боку, вирішує проблему врахування «тіла» колони, тобто «зрізаються» піки моментів, що виникають при моделюванні опирання на колону як на точкову опору. З іншого боку, забезпечує сприйняття колоною крутних деформацій. У більшості ж випадків, коли є принаймні хоч би дві колони, цього не вимагається, оскільки крутний момент від деформацій в площині плити в цьому випадку сприйматиметься парами поперечних сил в колонах, а крутні моменти будуть малими і ними можна знехтувати.
Сполучення стержня рами з діафрагмою
Якщо до формування дискретної розрахункової схеми підходити чисто формально, описуючи пластину сукупністю скінченних елементів плоского напруженого стану, а стержневий каркас одновимірними елементами, і не робити жодних додаткових заходів, то в ригелях, що примикають до вузлів сполучення каркаса з діафрагмою, як згинні моменти, так і повздовжні і поперечні сили виходитимуть довільними.
Тут труднощі обумовлені тим, що скінченні елементи плоского напруженого стану (балки-стінки) не мають ступеня свободи відповідного куту повороту відносно осі, що перпендикулярна площині діафрагми. Оскільки програмний комплекс зажадає формального виконання всіх умов рівноваги, у тому числі і рівноваги кожного з вузлів по моментах, то ригелі, що жорстко примикають до вузлів діафрагми, зобов’язані будуть передати на вузли строго нульові моменти. В результаті згинні моменти в ригелях в цих вузлах виявляться рівними нулю, що відповідає розрахунковій схемі з шарнірним приєднанням ригелів до діафрагми.
Нехай, сталевий ригель певного перерізу заведений на частини своєї довжини в цегельну стіну, як це показано на рис. 5.7, а. Тоді в розрахунковій схемі, у тому числі і в дискретному її аналогу, досить врахувати проникаючий на відповідну довжину в область плоскої задачі одновимірний елемент-стержень.
Інший варіант розрахункової схеми можна запропонувати в разі монолітного сполучення залізобетонної стінної панелі і ригеля каркаса будівлі (рис. 5.7, б). Тут можна врахувати фактичні розміри перерізу – висоту ригеля, вздовж якої на межі діафрагми доречно розмістити абсолютно жорстке тіло.
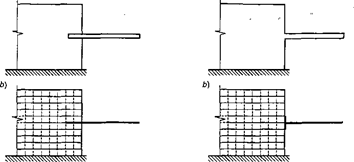
Рисунок 5.7 – Защемлення балки в стіні (а) та монолітне спряження ригеля з
діафрагмою (б)
Шрифти
Розмір шрифта
Колір тексту
Колір тла
Кернінг шрифтів
Видимість картинок
Інтервал між літерами
Висота рядка
Виділити посилання
Вирівнювання тексту
Ширина абзацу