Лекція 1.1 Загальні питання про спеціалізовані програмні продукти

6.1. Математичні моделі

Одним зі способів розв’язування багатьох наукових та виробничих задач є експеримент. Нехай за запропонованим проектом створено новий телефон, лі так, автомобіль, виробнича установка чи інший об’єкт. Виміряємо у створених об’єктів характеристики, які нас цікавлять. Якщо ці характеристики виявилися невдалими, то слід змінити проект ізнову створити ці об’єкти й так повторювати до здобуття сподіваних результатів. Зрозуміло, що це надто повільний і дорогий спосіб.

Іншим, дешевшим способом, є створення зменшеного чи збільшеного макета об’єкта й дослідження його поводження за різних умов. Цей спосіб називають фізичним моделюванням. У цьому разі виникають проблеми щодо відтворювання всіх реальних впливів на досліджуваний об’єкт.

Існує ще один спосіб - математичний аналіз об’єкта (конструкції чи процесу). У цьому разі на першому етапі розв’язування задачі слід математично описати поводження об’єкта, тобто окреслити його математичну модель. Математична модель зазвичай складається зрівнянь різної форми, які описують об’єкт дослідження. Прикладом, швидкість ракети за вертикального польоту у вакуумі визначається рівнянням

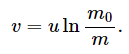 1,1

де M0 - початкова маса ракети; m - задана витрата пального.

Кожне досліджуване явище є надто складне. Воно пов’язано з іншими явищами природи, які можуть не становити інтересу для розв’язуваної задачі.

Перший етап моделювання об’єкта полягає в обиранні проектувальником зав'язків та характеристик явища, які треба долучити до математичної моделі як найбільш істотні для певної задачі. Якщо математичну модель обрано недостатньо ретельно, то висновки можуть виявитися цілковито помилковими. Приміром, рівняння 1,1 є непридатне для запуску ракети із Землі, оскільки в ньому не враховано опір повітря.

Другий етап роботи проектувальника - це математичне дослідження моде лі об’єкта. Залежно від форми й складності моделі застосовуються різні математичні методи. Для спрощених і нескладних математичних моделей часто вдається обчислити аналітичний розв’язок (тобто розв’язок, здобутий шляхом математичних перетворювань над символами).  

Через спрощену модель точність такого розв’язку є невелика. Для більш точних і складних моделей аналітичний розв’язок вдається обчислити не надто часто. У таких випадках застосовують чисельні методи, які найчастіше дозволяють дістати якісний опис об’єкта.