Лекція 1.3 MATLAB у задачах прикладної математики
2. Розв’язок системи лінійних алгебраїчних рівнянь методом виключення Гаусса
До розв’язання систем лінійних рівнянь зводяться численні практичні задачі, наприклад різні крайові задачі для звичайних і в частинних похідних диференційних рівнянь. Можна стверджувати, що проблема є однієї з найпоширеніших і важливих задач прикладної математики.Нехай задана система п лінійних алгебраїчних рівнянь з n невідомими:
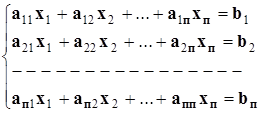3.1
Система рівнянь (3.1) у матричній формі представляється в такий спосіб:
АХ = Y, (3.2)
де: А – квадратна матриця коефіцієнтів, розміром п ´ п рядків і стовпців;
Х – вектор-стовпець невідомих;
В – вектор-стовпець правих частин.
Систему рівнянь (3.2) можна вирішити різними методами. Один з найбільш простих і ефективних – метод виключення Гаусса і його модифікації. Його алгоритм базується на приведенні матриці А до трикутнокового вигляду (прямій хід) і послідовному обчисленні невідомих (зворотний хід). Ці процедури можна виконувати над невиродженими матрицями, у противному випадку метод Гаусса не застосовується.
Недоліком методу є нагромадження похибок у процесі округлення, тому метод Гаусса без вибору головних елементів використовується звичайно для рішення порівняно невеликих (п £ 100) систем рівнянь із щільно заповненою матрицею і не близьким до нуля визначником.
Якщо матриця А сильно розріджена, а її визначник не близький до нуля, то метод Гаусса придатний для рішення великих систем рівнянь. У MATLAB мається великий арсенал методів рішення систем рівнянь (3.2) методом виключення Гаусса. Для цього застосовуються наступні оператори:
|
/ |
- правий розподіл; |
|
|
|
|
\ |
- лівий розподіл; |
|
|
|
|
^ - 1 |
- зведення в степінь –1; |
|
|
|
|
inv(A) |
- звертання матриці А. |
Вирази
|
Х |
= |
Y/A |
|
Х |
= |
Y* А^ - 1 |
|
Х |
= |
Y* inv(A) |
|
Х |
= |
A\Y |
дають рішення ряду систем лінійних рівнянь АХ = Y, де А – матриця розміром m × n, Y – матриця розміром n × к.
Приклад.
Розв’язати систему 4-х лінійних рівнянь:
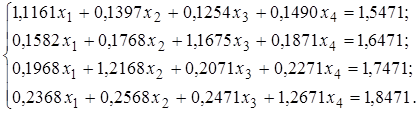
Протокол програми (у М-файлі)
|
а |
= |
[1.1161 0.1397 0.1254 0.1490 ; 0.1582 0.1768 1.1675 0.1871 ; 0.1968 1.2168 0.2071 0.2271 ; 0.2368 0.2568 0.2471 1.2671] ; |
|
b |
= |
[1.5471 ; 1.6471 ; 1.7471 ; 1.8471] ; |
<< Х4 = а \ b
Ця програма видає розв’язок заданої системи за допомогою четвертого оператора у виді матриці – стовпця:
|
Х4 |
= |
1.0406 0.9351 0.9870 0.8813 |
Увага. У М-файлі матриця а набирається по рядках, а елементи матриці правих частин b відокремлюються символом “;” , тобто теж набираються по рядках. Рішення іншими операторами системи рівнянь (3.2) вимагає набору матриці а по стовпцях, а елементи правих частин b відокремлюються тільки пробілом!
|
а |
= |
[1.1161 0.1582 0.1968 0.2368 ; 0.1397 0.1768 1.2168 0.2568 ; 0.1254 1.1675 0.2071 0.2471 ; 0.1490 0.1871 0.2271 1.2671] ; |
|
b |
= |
[1.5471 1.6471 1.7471 1.8471] ; |
<< Х1 = b/а
<< Х2 = b* a ^ - 1
<< Х3 = b* inv(a)
Результати розв‘язку:
|
Х1 |
= |
1.0406 0.9351 0.9870 0.8813 |
|
Х2 |
= |
1.0406 0.9351 0.9870 0.8813 |
|
Х3 |
= |
1.0406 0.9351 0.9870 0.8813 |
Шрифти
Розмір шрифта
Колір тексту
Колір тла