Лекція 1.3 MATLAB у задачах прикладної математики

5. Наближене обчислення визначених інтегралів

До обчислень визначених інтегралів зводиться багато практичних задач фізики, хімії, екології, механіки й іншій природних наук. На практиці формулою Ньютона-Лейбніца не завжди вдається скористатися. У цьому випадку використовуються методи чисельного інтегрування. Вони базуються на наступних підходах: з геометричної точки зору визначений інтеграл  являє собою площу криволінійної трапеції. Ідея методів чисельного інтегрування зводиться до розбивки інтервалу [a; b] на безліч менших інтервалів і перебуванню шуканої площі як сукупності елементарних площ, отриманих на кожному частковому проміжку розбивки. У залежності від використаної апроксимації виходять різні формули чисельного інтегрування, що мають різну точність. Розглянемо методи трапецій і Сімпсона (парабол).

Метод трапецій.

Тут використовується лінійна апроксимація, тобто графік функції y = f(x) представляється у вигляді ламаної, з'єднаної точками y_i. Формула трапецій при постійному кроці , де n – число ділянок, має вигляд:

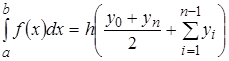.                             (3.8)

У MATLAB цю формулу реалізує програма trapz (x,y).

Метод Сімпсона

Якщо підінтегральну функцію замінити параболою, то формула Сімпсона з постійним кроком інтегрування:

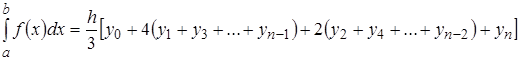.(3.9)

У MATLAB формула Сімпсона реалізується програмою quad, Підінтегральна функція може задаватися за допомогою дескриптора @, тоді вона програмується у файлі – функції, або за допомогою апострофів, тоді вона записується у самій програмі quad. Точність обчислення інтегралів за замовчуванням прийнята рівною 1×10^-6.

Приклад.

Обчислити за методами трапецій і Сімпсона значення інтеграла

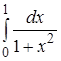
Протокол програми методу трапецій

>> x = 0 : 0.0001 : 1.0 ;

>> y = 1./ (1+x.^2) ;

>> z = trapz(x, y)

Результат обчислень

z =

        0.7854

Протокол програми методу Сімпсона

>> quad ( ¢ (1./(1+x.^2)) ¢, 0, 1)

Результат обчислень

ans =

0.7854

Точне значення інтегралу дорівнює 0,785398163.

Як видно з прикладу отримані результати є практично точними, а самі протоколи досить прості.