Чисельне рішення оптимізаційних задач

1. Чисельне рішення оптимізаційних задач

Під оптимізацією розуміють процес вибору найкращого варіанта з усіх можливих. З погляду інженерних розрахунків методи оптимізації дозволяють вибрати найкращий варіант конструкції, найкращий розподіл ресурсів, мінімальні збитки природному середовищу і т.п. У процесі розв’язку задачі оптимізації необхідно знайти оптимальні значення деяких параметрів, які називають проектними параметрами. Вибір оптимального рішення проводиться за допомогою деякої функції – цільової функції. Її можна записати у вигляді:

,                                    (4.1)

де: х₁, х₂, … , х_п – проектні параметри,

Можна виділити два типи задач оптимізації – безумовні й умовні. Безумовне завдання оптимізації полягає у пошуку максимуму або мінімуму функції 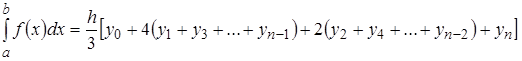 від n дійсних змінних і визначені відповідних значень аргументів на деякій множині G n-мірного простору. Звичайно розглядаються задачі мінімізації; до них легко зводяться і задачі на пошук максимуму шляхом заміни знака цільової функції на протилежний. Умовні задачі оптимізації – це такі, при формулюванні яких задаються деякі умови (обмеження) на множині G. Тут розглянемо тільки безумовні задачі оптимізації.