Чисельне рішення оптимізаційних задач

1.2. Пошук мінімуму функцій декількох змінних

Дана задача значно складніше попередньої. Розглянемо її рішення на прикладі функції двох змінних. Алгоритм можна використати для функцій більшого числа змінних. Для мінімізації функцій декількох змінних MATLAB застосовує симплекс – метод Нелдера-Міда. Такий метод є одним із кращих методів пошуку мінімуму функцій багатьох змінних, коли не обчислюються похідні або градієнт функції. Він зводиться до побудови симплекса в п-мірному просторі, заданого п + 1 вершиною. У двомірному просторі симплекс є трикутником, а в тривимірному – пірамідою. На кожному кроці ітерацій вибирається новий розв’язок всередині або поблизу симплексу. Він порівнюється з однієї з вершин симплекса. Найближча до нього вершина симплекса заміняється розв’язком. Таким чином, симплекс перебудовується і дозволяє знайти нове, більш точне положення розв’язку. Алгоритм пошуку повторюється, поки розміри симплексу за всіма змінними не стане менше заданої помилки.

Функцію, що реалізує симплекс-метод Нелдера-Міда, зручно використовувати в наступному записі:

[x, min f] = f min search ( … ),

де: х – вектор координат локального мінімуму;

minf – значення цільової функції в точці мінімуму.

Саму цільову функцію зручно представити за допомогою дескриптора @ у М-файлі.

Приклад.

Знайти координати і значення мінімуму функції двох змінних f(x, y) = (x²+ + y² – 3)² + (x² + y² – 2x – 3)² + 1, якщо початкова точка пошуку має координати М₀ (1; 1). Аналіз функції показує, що min f = 1 x = 0, .

Будуємо тривимірний графік цієї функції, щоб переконатися в наявності мінімуму. Візьмемо інтервал х є [-1; 1]; y є [1; 3].

Протокол програми

>> [x,y] = meshgrid ( [-1 : 1, 1 : 3] ) ;

>> z=(x.^2+y.^2-3).^2+(x.^2+y.^2-2*x-3).^2+1;

>> рlot 3 (x,y,z) (рис. 4.2)

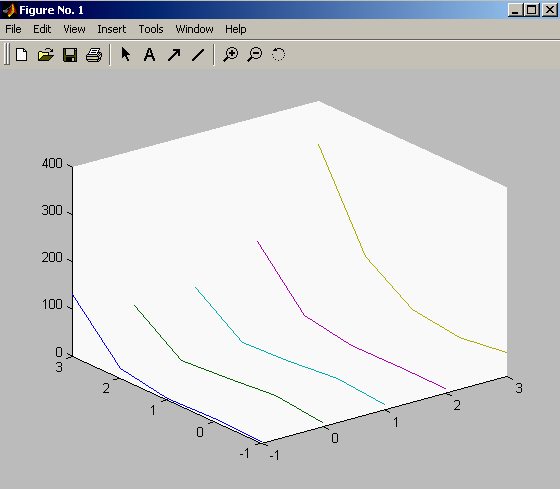
Рис. 4.2. Поверхня функції f(x, y) = (x²+ + y² – 3)² + (x² + y² – 2x – 3)² + 1

Після побудови тривимірного графіка виконуємо пошук мінімуму, у М-файлі програмуємо цільову функцію:

function f = Fxy(x)

f = ((x(1)^2+x(2)^2-3)^2-3)^2+((x(1)^2+x(2)^2-2*x(1)-3)^2)+1;

Вирішуємо поставлену задачу у вікні команд:

>> [xmin, minf] = fminsearch ( @Fxy, [1; 1] )

Результати пошуку

xmin =

              - 0.0000     1.7320

 minf =

              1.0000

Як видно, результати рішення задачі точні.