Чисельне рішення оптимізаційних задач

2. Пакет оптимізації Optimization Toolbox

Пакет оптимізації (Optimization Toolbox) – це бібліотека функцій, що розширюють можливості системи MATLAB за чисельними обчисленнями і призначена для рішення задач оптимізації і систем нелінійних рівнянь. Підтримує основні методи оптимізації функцій ряду змінних:

• безумовна оптимізація нелінійних функцій;
• метод найменших квадратів;
• розв’язок нелінійних рівнянь;
• лінійне програмування;
• квадратичне програмування;
• умовна мінімізація нелінійних функцій;
• методи мінімакса;
• багатокритеріальна оптимізація.

Розглянутий пакет дає можливості вирішувати задачі мінімізації функцій, перебору розв’язку рівнянь, задачі апроксимації («припасування» кривих під експериментальні дані).

Різні типи таких задач разом із застосовуваними для їхнього рішення функціями пакету (Optimization Toolbox) приведені в таблиці 5.1.

Таблиця 5.1.

Типи задач, розв'язуваних засобами пакета Optimization Toolbox

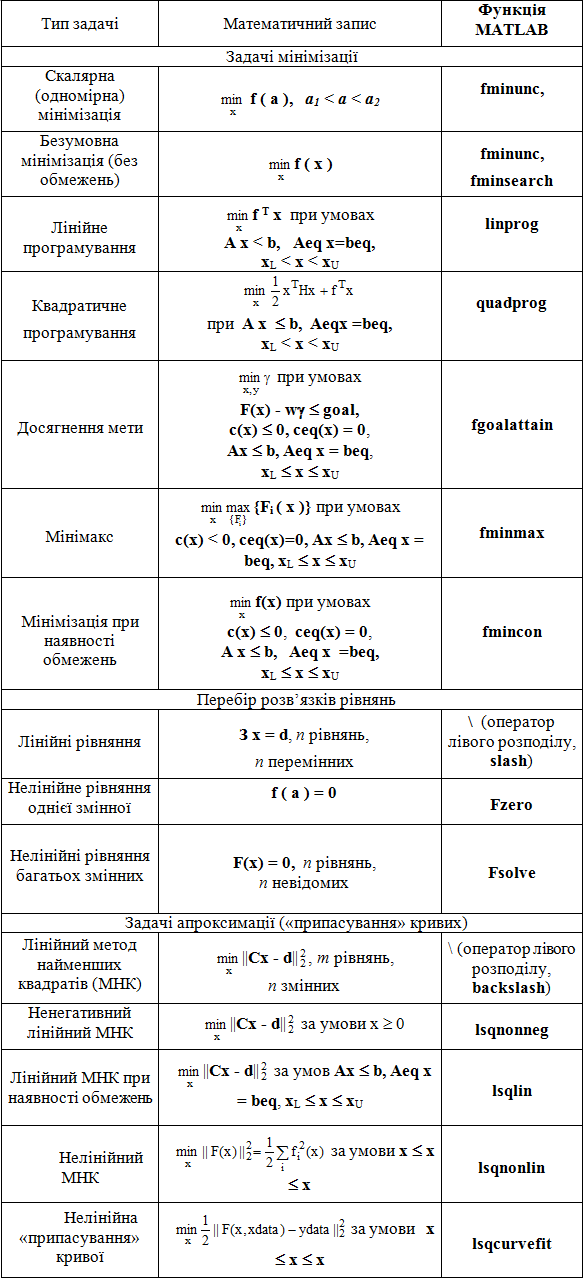
Прийняті позначення: а – скалярний аргумент; х, у – у загальному випадку векторні аргументи; f(а), f(х) – скалярні функції; F(x), c(x), ceq(x), K(x, w) – векторні функції; •А, Aeq, З, Н – матриці; b, beq, d, f, w, goal, xdata, ydata – вектори.

У рамках пакета Optimization Toolbox усі задачі оптимізації поділяються на дві групи: задачі малої і середньої розмірності і задачі великої розмірності. Відповідно, такий же розподіл прийнятий для алгоритмів рішення таких задач. Зрозуміло, це не означає, що для розв’язку задач середньої розмірності не можна застосовувати алгоритми великої розмірності і навпаки. Просто алгоритми тієї або іншої групи більш ефективні для задач своєї розмірності.

У пакеті (Optimization Toolbox) реалізовано широкий набір алгоритмів для рішення задач оптимізації середньої і малої розмірності. Основними для задач без обмежень є симплексний метод Нелдера-Міда і квазіньютоівскі методи. Для рішення задач з обмеженнями, мінімакса, досягнення мети і використані алгоритми квадратичного програмування.

Задачі, що зводяться до нелінійних МНК, вирішуються за допомогою алгоритмів Ньютона-Рафсона і Левенберга-Марквардта.

Допоміжні процедури одномірної (скалярної) оптимізації використовують алгоритми квадратичної (параболічної) і кубічної інтерполяції.

Розглянемо найбільше часто застосовувані в задачах оптимізації функції  лінійного (linprog) і нелінійного (fmincon) програмування.