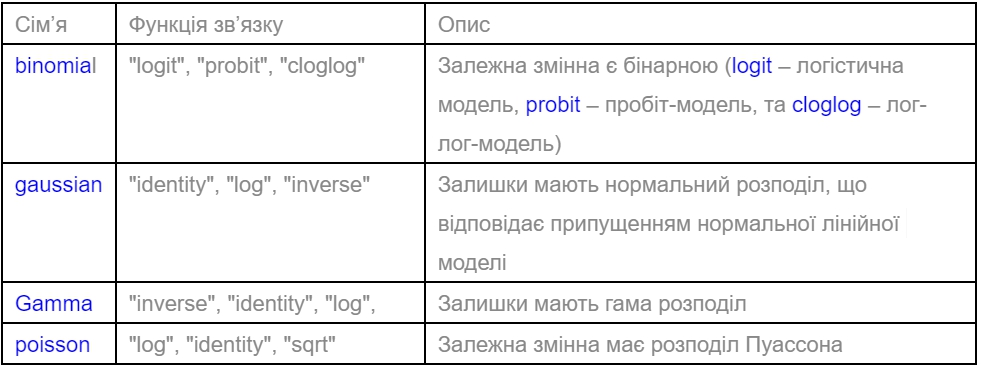
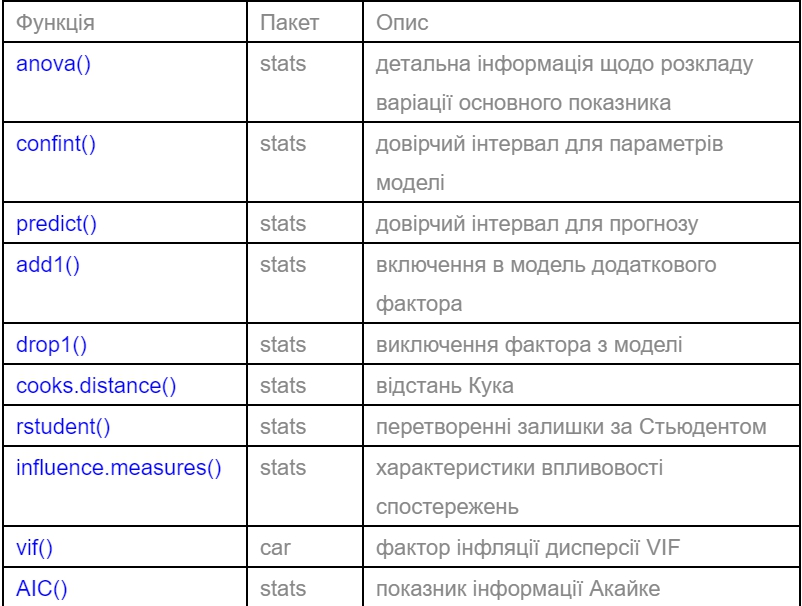
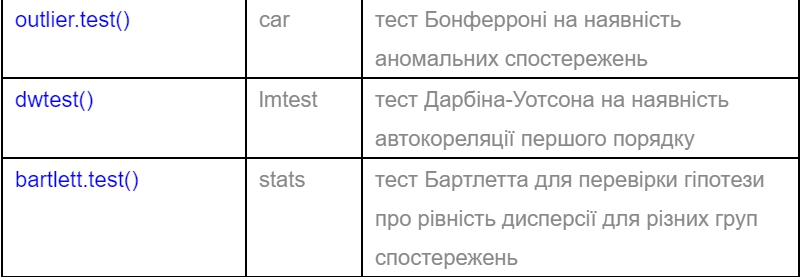
Тема 2. Алгоритми Data Mining: класифікація і регресія

2. Регресія в Data Mining

Регресією називають апроксимацію даних з врахуванням їх статистичних параметрів. Таке завдання постає при обробці даних, отриманих в результаті вимірювань процесів або фізичних явищ. Завданням регресійного аналізу є підбір математичних формул, які найкращим чином можуть описати заданий набір.

Математична постановка задачі регресії полягає в наступному. Залежність величини певної властивості об’єкту Y від іншої змінної властивості або параметра Х зареєстровано на множині точок множиною значень. В кожній точці зареєстровані значення відображені з випадковою похибкою. За сукупністю значень потрібно підібрати таку функцію, яка б з мінімальною похибкою відображала зареєстровані дані.

Передумови кореляційно-регресійного аналізу

• Чітке уявлення про причинно-наслідкові зв’язки між досліджуваними ознаками
• Достатня варіація досліджуваних ознак
• Якісна однорідність досліджуваних сукупностей
• Досить велике число спостережень
• Випадковість і незалежність одиниць сукупності одна від одної.
• Досліджувані ознаки повинні мати кількісний (числовий) вираз

Види регресії називаються за типом апроксимуючих функцій: поліноміальна, експоненціальна, логарифмічна.

• Прості (парні) зв’язки:

у = а₀ + а₁х – лінійний.

• Нелінійні :

у = а₀ + а₁х + а₂х² – парабола 2-го порядку.

у = а₀ +а₁ / х – гіпербола.

у = а₀ х^а1 – степенева функція.

у = а₀ а₁^х – показникові функція.

у = а₁ lnx +а₀ – логарифмічна.

• Множинні зв’язки:

у = а_о +а₁х₁+а₂х₂ +… +а_nх_n – лінійний.

у = а_о +а₁х₁² + а₂х₂² + … + а_nх_n² – нелінійний.

у = а_о х₁^а1х₂^а2 – нелінійна виробнича функція Кобба-Дугласа.

у = а_ох₁^а1х₂^а2… х_m^am – загальна виробнича функція Кобба-Дугласа.

Вибірку даних, найчастіше, представляють у вигляді масиву, що складається з пар чисел (x_i , y_i). Тому, виникає завдання апроксимації дискретної залежності y (x) безперервною функцією f (x). Функція f (x), залежно від специфіки завдання, може відповідати різним вимогам:

• f (x) повинна проходити через точки (x_i , y_i) , тобто f (х_i ) = у_i , i = 1 ... n. В цьому випадку  говорять про інтерполяцію даних функцією f (х) між точками х_i, або екстраполяції за межами інтервалу, що містить всі х_i.
• f (х) повинна наближати експериментальну залежність y (x_i), враховуючи, що дані (x_i, y_i) отримано з деякою погрішністю, що виражає шумову компоненту вимірювань. При цьому функція f (х), за допомогою того чи іншого алгоритму, зменшує похибку, що присутня в даних (x_i, y_i). Такого типу задачі називають фільтрацією.
• f (х) повинна певним чином (наприклад, у вигляді певної аналітичної залежності) наближати y (x_i), не обов'язково проходячи через точки (x_i, y_i). Таку постановку завдання регресії в багатьох випадках можна назвати згладжуванням функції.

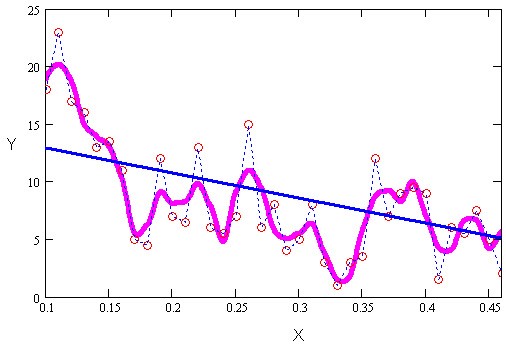
На рисунку проілюстровано різні види побудови апроксимуючої залежності f (х). Тут, вихідні дані позначено точками, інтерполяція - пунктиром, фільтрація - жирною гладкою кривою, а лінійна регресія (згладжування) - похилою прямою лінією.

Базовими функціями для оцінки параметрів регресійної моделі є функція lm() (застосовують для одержання оцінок коефіцієнтів лінійної моделі методом найменших квадратів) та функція glm() (застосовують для отримання оцінок параметрів узагальнених лінійних моделей).

Одним з основних аргументів даних функцій є аргумент formula, який визначає вигляд рівняння регресії, параметри якої мають бути оцінені. Для функції glm() основним аргументом також є аргумент family, який визначає конкретний тип розподілу експоненціальної сім’ї, що мають залишки, та тип функцію зв’язку – link.

 Функції повертають об’єкти, що є списками з цілою низкою полів, що визначають різні характеристики моделі, зокрема поле сoefficients визначає значення оцінених параметрів, residuals – залишки моделі, а поле fitted.values – розрахункові значення моделі. Крім того, для даних об’єктів наявні різні методи, що дозволяють модифікувати модель, визначати різні характеристики адекватності, перевіряти припущення моделі, тощо.

Для зручного представлення результатів оцінювання параметрів можна використати функцію summary(), що фактично є методом класу lm.