ЛЕКЦІЯ 6. ОСНОВИ ТЕОРІЇ ПЕРСПЕКТИВИ
| Сайт: | Навчально-інформаційний портал НУБіП України |
| Курс: | Фотограмметрія та дистанційне зондування ☑️ |
| Книга: | ЛЕКЦІЯ 6. ОСНОВИ ТЕОРІЇ ПЕРСПЕКТИВИ |
| Надруковано: | Гість-користувач |
| Дата: | середа, 21 січня 2026, 18:15 |
1. Центральна проекція знімка та ортогональна проекція плану
Побудова зображення об¢єкта (предмета) на будь-якій поверхні за визначеним законом називається проектуванням, а одержане зображення – проекцією об’єкта(предмета). Землевпорядник у своїй діяльності має справу в основному з двома видами проекцій - ортого-нальною і центральною. З геометричного погляду фотографування - є процес проектування множини точок об’єкта на площину негатива через об’єктив, вузлова точка якого є центром проектування.
У геодезії для одержання проекції невеликої ділянки земної поверхні всі точки проектують на горизонтальну площину прямовисними лініями. Такий спосіб проектування називається прямокутним, або ортогональним, а одержана проекція – ортогональною. Якщо точки простору проектувати на будь-яку поверхню Е променями, які виходять з однієї точки S, яка називається центр проекції, то такий спосіб проектування називається центральним (див. рис2.6б).
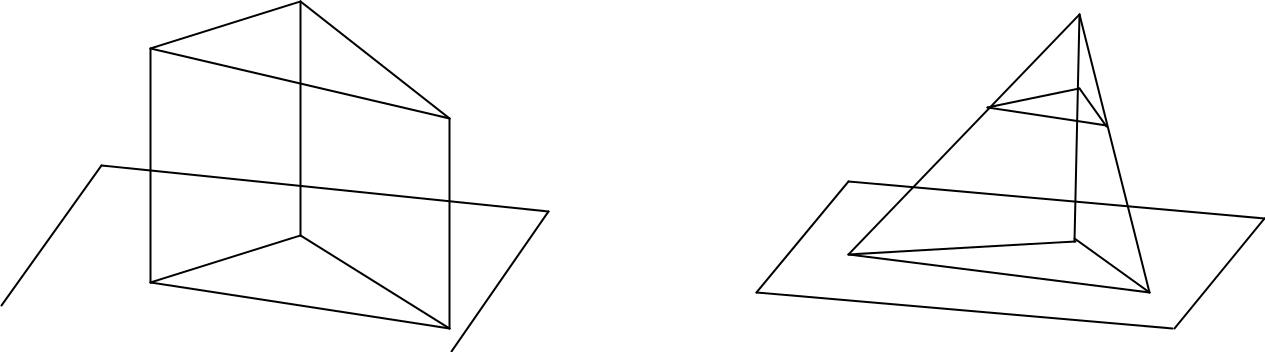
Рис.1. Види проекцій:а ортогональна; б центральна
Таким чином, аерофотознімок являє собою центральну проекцію фотографованого об’єкта. Центральна проекція ще називається перс-пективою об’єкта. Нехай А, В, С і D (рис. 2.7) - точки місцевості, а S- центр проекції. Тоді точки перетину а, в, с, d площини Р проектують променями AS, BS, CS і DS, є центральні проекції відповідних точок місцевості. Таку ж саму центральну проекцію можна побудувати й у тому разі, якщо площину проекції Р¢ провести з іншого боку від центру проектування і на тій же відстані від нього.
Оскільки негатив і позитив розміщуються симетрично щодо центру проекції, то вони однакові (конгруентні). Зазначимо, що зображення об'єкта на площині знімка, одержане в центральній проек-ції, називається перспективним зображенням.
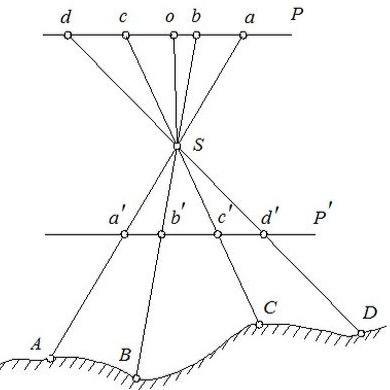
Рис. 2. Ортогональна (горизонтальна) проекція
Якщо центр проектування перенести на нескінченно велику відстань щодо місцевості, то проектувальні промені будуть взаємно паралельними. Їхній перетин з перпендикулярною до них площиною дає ортогональну проекцію точок місцевості. У топографії така проекція (за умови, що проектують прямовисні промені) називається горизонтальною.
Відмінність між ортогональною (горизонтальною) і центральною проекціями показано на рисунку 2.8. Точки місцевості A, B, C і D зображуються на площині Р у центральній проекції в точках a, b, c, d, а в ортогональній - у точках aо, bо, cо, dо. При переміщенні площини проекції в положення Р’’ взаємне положення точок aо, bо, cо, побудованих в ортогональній проекції, не порушиться.
2. Елементи центральної проекції
Основними елементами центральної проекції є
S – центр проектування – точка, з якої виходять або в якій перетинаються всі проектувальні промені;
Е – предметна площина – площина, у якій розташовані об’єкти, що проектуються (у разі АФЗ це - місцевість);
Р – картинна площина (картина), у якій створюється зображення предмета (у разі АФЗ це – знімок чи негатив);
ТТ – основа картини, або вісь перспективи, – лінія перетину предметної та картинної площин;
W – площина головного вертикала – прямовисна площина, що проходить через центр проекції перпендикулярно до осі перспективи;
E'– площина дійсного горизонту – площина, проведена через центр проектування S паралельно предметній площині;
vv0 – головна вертикаль – лінія перетину площини головного вертикала з картинною площиною.
Vv0– проекція головної вертикалі (в фотограмметрії – лінія напрямку знімання) лінія перетину площини головного вертикала і предметної площини;
hihi – лінія дійсного горизонту – лінія перетину площини дійсного горизонту з картинною площиною;
То – головна точка картинної площини (картини) – основа перпендикуляра, який опущено з центру проекції на картинну площину. Головна точка завжди лежить на головній вертикалі;
So – головний промінь. Відстань So – головна віддаль – фокусна віддаль картини (у разі аерофотознімання це – фокусна віддаль аерофотоапарата (So = f);
О – проекція головної точки картини на предметну площину – перетин головного променя з предметної площиною;
n – точка надира – точка перетину прямовисної лінії з головною вертикаллю (з картиною);
N – проекція точки надира n на предметну площину – перетин прямовисної лінії з проекцією головної вертикалі (з предметною площиною). Віддаль SN – висота центру проектування над предметною площиною. Для аерофотознімання SN = H – висота фотографування;
с – точка нульових спотворень – перетин бісектриси кута oSn з головною вертикаллю;
С – проекція точки нульових спотворень на предметну площину (перетин лінії Sc із проекцією головної вертикалі;
v0 – головна точка основи картини (осі перспективи) – точка перетину головної вертикалі та її проекції з віссю перспективи;
α – кут нахилу картинної площини відносно предметної. У загаль-ному випадку картинна площина займає довільне положення відносно предметної.
Залежно від розміщення площини Р відносно центру проектування - картинна площина може бути позитивною (коли вона знаходиться між центром проектування і предметною площиною) або негативною (коли центр проектування розташований між предметною і картинною площинами);
і – головна точка збіжності – точка перетину головної вертикалі з лінією дійсного горизонту.
Будь-яка лінія, проведена в картинній площині перпендикулярно до головної вертикалі ( й відповідно паралельно осі перспективи), називається горизонталлю.
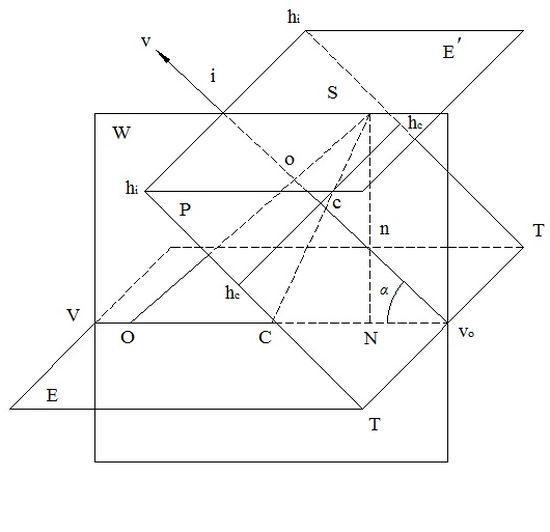
Рис. 3. Елементи центральної проекції
Горизонталь, проведена через головну точку картини, називається головною горизонталлю h0 h0.
Горизонталь, проведена через точку нульових спотворень, називається лінією неспотворених масштабів hc hc .
Горизонталь, проведена через надирну лінію, називається надирною лінією.
Між елементами центральної проекції існують залежності:
3. Властивості перспективних зображень
Властивості центральної проекції:
- перспективним зображенням будь–якої точки місцевості, скажімо А, є точкаа і притому єдина (див. рис. 2.10). Будь-якій точці знімка, наприклад, а відповідає безліч точок місцевості A, A1 і т.д.
- перспективним зображенням будь-якої прямої простору, нап-риклад ВС, яка не проходить через центр проекції, є пряма bc і притому єдина. Але вона зобразилася б точкою, якби розта-шовувалася на проектувальному промені, скажімо пряма DK і точка d (або k).
Будь-якому відрізку на знімку, наприклад bc, відповідає незліченна кількість відрізків місцевості BC, B 1C1 і т.д.
- Відрізки продовжують до перетину з лінією основи картини. Одержані точки належать двом площинам - площині основи і площині знімка (картини).
- На площині знімка знаходять положення головної точки збіжності J і будують лінію hihi перпендикулярну до головної вер-тикалі (лінію дійсного горизонту).
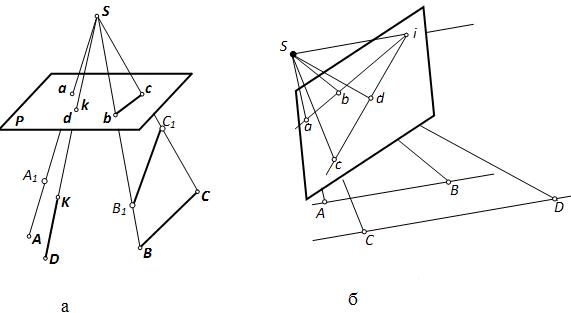
Рис.4. Перспективне зображення: а – точки місцевості, б – прямого простору
- Через центр проекції S проводять промінь, паралельний заданим відрізкам. Він буде розміщений у площині дійсного горизонту. Перетин цього променя з лінією hihi визначає точку збіжності J¢ зображень відрізків.
- З'єднують прямими лініями точку J¢ з точками, одержаними на лінії основи картини. Ці лінії на знімку є зображення променів, що йдуть від лінії основи картини через задані відрізки до безкінечності.
- Проектують промені через точки, що обмежують відрізки. Їхній перетин із побудованими на знімку лініями й визначає шукане зображення.
Точка збіжності зображень вертикальних (прямовисних) прямих збігається з точкою надира n. Перетин Bо відрізка АВ із площиною знімка є на вертикальній площині, що проходить через пряму АВ, і паралельній площині головного вертикала. Тому відрізок NBо є зобра-женням нескінченного прямовисного променя, який іде з точки Bо.
4. Епюри. Теорема шаля
Розрізняють епюри розтягнення і складання. Якщо предметну площину E обертати навколо основи картини ТТ так, щоб кут між цими площинами становив 180°, а площину дійсного горизонту E' обертати навколо лінії дійсного горизонту hi hi так, щоб кут між картинною площиною й площиною дійсного горизонту також становив 180°, то матимемо епюр розтягнення (рис. 2.13а,б). На епюрі розтягнення всі три площини продовжують одна одну.
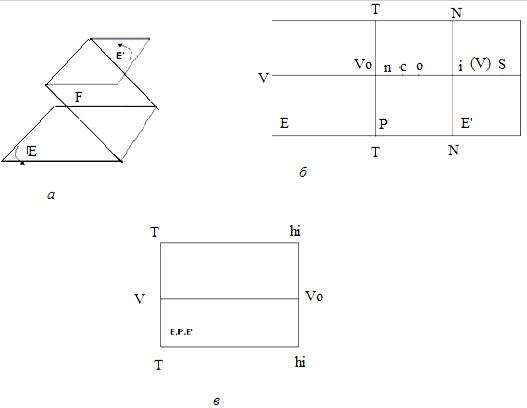
Рис. 5. Епюри: а, б – розтягнення; в – складання
Епюр складання утворюється, якщо предметну площину і площину дійсного горизонту обертати в протилежні порівняно з епюром розтягнення сторони до збігу всіх трьох площин в одну (кут між площинами дорівнює 0).
Для дослідження масштабу перспективного зображення скористаємося перспективою сітки квадратів, в якій одна з сторін збігається з віссю перспективи ТТ , а інша – з проекцією головної вертикалі voV (рис. 2.14).
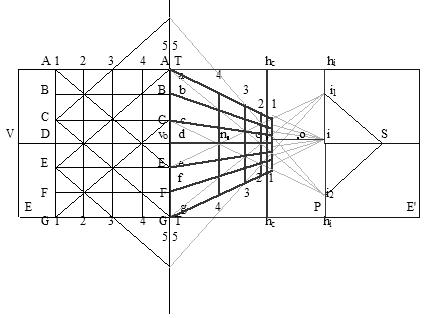
Рис. 6. Перспектива сітки квадратів на епюрі розтягнення
В загальному випадку масштаб перспективи є зміною величиною змінна.
Аналізуємо цей масштаб :
- масштаб перспективи на її осі ТТ дорівнює одиниці : 1/m = k2k3 / K2 K3 = 1;
- масштаб на одній і тій же самій горизонталі є величиною постійною: ab = bc = … = 1/m2 = const;
- масштаб перспективи на лінії дійсного горизонту hihi дорівнює нулю:1/m3 = 0 / k2k3 = 0;
- масштаб перспективи уявно продовжується й нижче осі перспективи ТТ і буде збільшуватиметься до нескінченності: 1/mn = ¥ /A1B1 = ¥ ;
- масштаб у головній точці збіжності і за напрямком головної вертикалі дорівнює нулю: 1/m1= 0;
- масштаб по горизонталі, що проходить через точку с завжди дорівнюватиме масштабу горизонтального аерофотознімка і називається головним масштабом: 1/mc = f/H;
- масштаб по лінії головного вертикала є змінним і змінюється від 1 у точці vo до 0 в точці і .
Теорема Шаля (Теорема про незмінність перспективи). Якщо обертати площину Т навколо основи картини tt’, а площину Е навколо лінії дійсного горизонту ii’, зберігаючи їх взаємну паралельність, то перспектива всякої точки А залишиться незмінною.
5. Перспектива кута
Розглянувши перспективу сітки квадратів необхідно відмітити, що утворені сторонами сітки прямі кути змінилися у перспективі однаково як у бік збільшення, так і в бік зменшення.
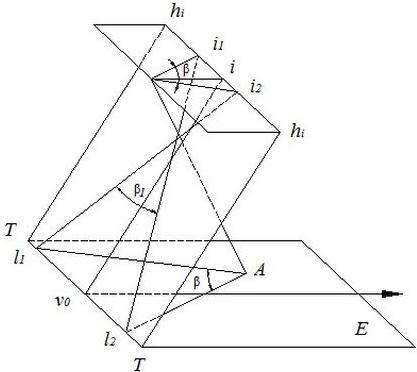
Рис. 6. Перспектива кута
6. Питання для самоконтролю
- Назвіть властивості ортогональної та центральної проекцій.
- Які основні площини центральної проекції?
- У якому випадку зображення, побудовані у центральній проекції, відповідають зображенням, побудованим в ортогональній проекції?
- Якій відстані у центральній проекції відповідає висота фотографування при аерофотозніманні?
- Перспективи яких ліній перетинаються в головній точці збіжності?
- У якій точці картинної площини масштаб найменший і в якій найбільший?
- Покажіть напрямки осей координатної системи на просторовому кресленні центральної проекції.
7. Питання на самостійну підготовку
- Масштаб перспективи
- Перспектива точок, ліній і просторових фігур
- Види проекцій
Шрифти
Розмір шрифта
Колір тексту
Колір тла
Кернінг шрифтів
Видимість картинок
Інтервал між літерами
Висота рядка
Виділити посилання
Вирівнювання тексту
Ширина абзацу