ЛЕКЦІЯ 7. СИСТЕМИ КООРДИНАТ, ЯКІ ВИКОРИСТОВУЮТЬ У ФОТОГРАММЕТРІЇ
| Сайт: | Навчально-інформаційний портал НУБіП України |
| Курс: | Фотограмметрія та дистанційне зондування ☑️ |
| Книга: | ЛЕКЦІЯ 7. СИСТЕМИ КООРДИНАТ, ЯКІ ВИКОРИСТОВУЮТЬ У ФОТОГРАММЕТРІЇ |
| Надруковано: | Гість-користувач |
| Дата: | вівторок, 3 березня 2026, 07:41 |
1. Системи координат, які використовують у фотограмметрії
У фотограмметрії положення точки місцевості визначаються за правою системою прямокутних координат Гауса Ог Хг Уг Zг так само, як і в геодезії, а також за лівою просторовою системою прямокутних координат OXYZ, що називається фотограмметричною (див. рис. 4.1).
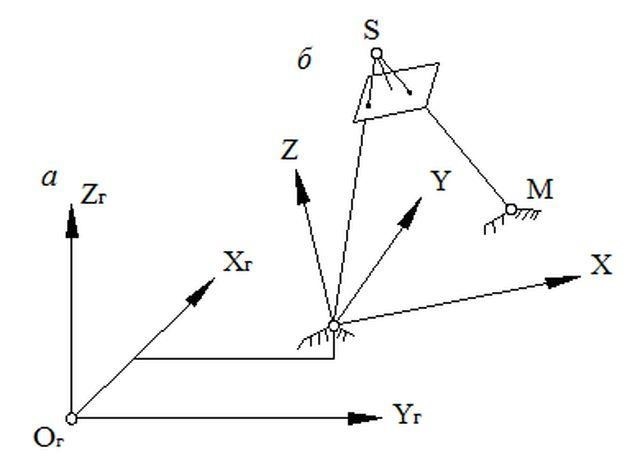
Рис.1 Геодезична система прямокутних координат (а) і фотограмметрична система (б)
В окремому випадку початок системи суміщають із будь-якою точкою місцевості, наприклад, точкою А, або з центром проекції S. Осі Х та Y вибирають паралельними осям х і у знімка.
Початок прямокутної системи координат o'xy знаходиться на перетині прямих, що з’єднують координатні мітки 1 і 2, 3 й 4. Вісь х суміщають із
прямою 1-2 (а) або проводять паралельно прямій 3-2(б).
Взаємне положення точок на аерознімку або космічному знімку часто встановлюють у прямокутній системі координат o'xy (рис. 4.2).
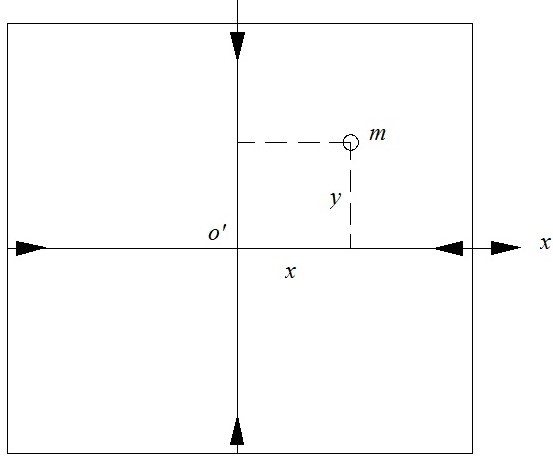
Рис 2. Прямокутна система координат
В ідеальному випадку, головна точка знімка повинна збігатися з точкою о', але цього важко досягти. Тому перехід від виміряних координат х' і y' до координат х і у здійснюють шляхом паралельного перенесення системи
координат о'x'y' на величини хо і уо:

Рис.3. Просторова прямокутна система координат
Для всіх точок знімка апліката z у системі Sxyz дорівнює – f. Координати точки m в системі Sxyz мають такі значення:
При розв’язанні фотограмметричних завдань на великі віддалі, а також при космічних дослідженях використовують праву геоцентричну систему
координат (див. рис. 4.4).
Початок цієї системи – в центрі земного еліпсоїда, вісь ZГ суміщена з полярною віссю О'ГР , а вісь X 'Г установлена в площині початкового меридіана.
Рис.4. Геоцентрична система координат
2. Фотограмметрична система координат
Визначено, що для рішення задачі в випадку невідомих елементів орієнтування (внутрішнього і зовнішнього орієнтування знімків стереопари), необхідно знати координати X, Y, Z мінімум п`яти опорних точок, які не розташовані в одній площині. При умові фотографування об'єкту двома синхронно працюючими відеокамерами і вимірюванні маркерів на цифрових знімках в автоматичному режимі, запропоновано для досліджень використати просторову фотограмметричну систему координат.
3. Залежність між системами координат точок знімка
При вивченні теорії фотограмметрії й розв’язанні практичних завдань використовують залежності між площинними координатами x, y точок знімка та їхніми просторовими координатами X', Y', Z'. Ці залежності можна встановити, якщо відомі елементи внутрішнього і кутові елементи зовнішнього орієнтування знімка. Координатні осі x, y цієї системи розміщують паралельно відповідним осям на знімку, а вісь z сумісна з головним променем зв'язки So.
Тоді координати x, y будь-якої точки знімка в просторовій системі мають ті ж самі значення, що й у плоскій, а координата z для всіх точок постійна і дорівнює фокусній віддалі знімка (z = f). Системи SX'Y'Z'і S x y z мають спільний початок, тому в процесі перетворення координат з однієї системи в іншу слід виконувати тільки обертання, що виражається, наприклад, формулою(4.2):
Для цього вводять систему координат S x y z і з початком у точці фотографування S
Ортогональна матриця А має третій порядок і називається матрицею перетворення координат. Її елементами є дев’ять направляючих косинуса, тому вище наведене співвідношення можна записати і так :
Причому кожен з напрямлених косинусів - це косинус кута між відповідними осями систем координат, які беруть участь у перетворенні, тобто :
Зазначимо, що в формулі (4.4) не добутки координат, укладених в дужках, а позначення осей, між якими береться кут.
Завдяки ортогональності напрямні косинуси матриці пов'язані між собою шістьма незалежними рівняннями :
Загальна матриця перетворення A дорівнює добутку:
А = Аα Аω АК
Після перемножування матриць одержують формули для обчислення напрямлених косинусів. При цьому вони матимуть вигляд:
Можна було б навести і ще ряд співвідношень. Перехід від просторових координат до плоских здійснюється за формулами:
де АТ - транспонована матриця А.
Якщо початок координат знімка не збігається з його головною точкою, то замість координат x та y у формулах 4.7, 4.8 і 4.9 слід використовувати різниці x - xо і y - yо. Формули 4.7 - 4.10 справедливі для будь-яких значень кутових елементів зовнішнього орієнтування знімка:
Для планових знімків, коли α, ω і малі, з точністю до членів другого порядку малості можна записати:
Одержані залежності між системами координат X 'Y' Z 'і xyz використовують в аналітичних способах визначення координат точок місцевості за вимірюваннями знімків.
4. Залежність між координатами точок місцевості і знімка
Точка місцевості М та її зображення на знімку т знаходяться на одному проектувальному промені (рис.4.9). Положення точок S і М у системі координат місцевості XYZ визначається векторами відповідно, а положення точок та М у системі координат SX 'Y' Z ' векторами. Вектори колінеарні, тому:
Рис.5.Схема зв’язку координат точок місцевості та знімка
Таким чином, якщо елементи орієнтування знімка дані, то два рівняння (4.16) мають три невідомих. Звідси випливає, що просторові координати точки місцевості за одиночним знімком не визначити. Можна одержати лише її планове положення. Але треба знати висоту фотографування H = - (Z - ZS). У фотограмметрії часто викорис-товують зворотні залежності (між координатами точки знімка і координатами відповідної точки місцевості). Для їх одержання, проектують вектори рівності на координатні осі системи координат S xyz (рис.
4.9), у результаті чого матимуть:
Розв’язують третє рівняння щодо λ і підставляють його значення в перше і друге рівняння. Тоді:
Матриці-стовпці рівностей можна представити у вигляді:
Підставивши вирази проекцій векторів r і R з (4.23),одержують:
Формули справедливі при будь-яких значеннях елементів орієнтування знімка.
Нехай xо = yо = 0, XS = YS = 0, ZS - Z = H, тоді за умови розташування осей (знімок можна вважати горизонтальним) формули матимуть такий вигляд:
де xо, yо - координати точки горизонтального знімка.
Якщо припустити, що знімок похилий, то при цьому матриця перетворення координат A виглядатиме так:
І при вище зазначених умовах (x0 = y0 = 0, XS = YS = 0, ZS - Z = H), одержуємо:
Рівняння (4.26) записані для випадку, коли початок координат на місцевості поєднаний з точкою S або N, а на знімку - з головною точкою о.
Якщо ж початок координат перенести відповідно до точки C і c, то співвідношення стануть ще простішими:
За умови, що за початок координат на місцевості прийнято точку N, а на знімку - відповідну їй точку надира n, то будуть справедливими такі співвідношення:
Рівняння легко одержати із співвідношення перенесенням систем координат на знімку і в просторі.
5. Питання для самоперевірки
- Системи координат точок місцевості
- Системи координат точок знімка
- Просторові системи координат точок знімка
- Залежність між просторовими і плоскими координатами точок аерознімка
6. Питання на самостійну підготовку
- Геоцентрична система координат. В яких випадках її використовують?
- Залежність між просторовими і плоскими координатами точок аерознімка.
- Система координат знімка.
Шрифти
Розмір шрифта
Колір тексту
Колір тла
Кернінг шрифтів
Видимість картинок
Інтервал між літерами
Висота рядка
Виділити посилання
Вирівнювання тексту
Ширина абзацу