Лекція 3. Електричнi кола постiйного струму
| Сайт: | Навчально-інформаційний портал НУБіП України |
| Курс: | Електротехніка в будівництві ☑️ |
| Книга: | Лекція 3. Електричнi кола постiйного струму |
| Надруковано: | Гість-користувач |
| Дата: | субота, 27 грудня 2025, 18:03 |
Опис
1. Еквівалентні перетворення в електричному колі постійного струму
В цьому розділі розглядатимемо виключно лінійні електричні кола при усталеному режимі. При включенні джерел живлення усталений режим електричного кола спостерігається не одразу – необхідний деякий час для переходу кола від попереднього до нового стану. Процеси, що відбуваються у колі під час переходу з одного стану до іншого, звуться перехідними процесами, а відповідний режим – перехідним режимом.
Наявність в електричному колі перехідного режиму пов’язана з неможливістю стрибкоподібних змінень струму в індуктивностях та напруги на ємностях, які входять до складу цього електричного кола. Отже при дослідженні усталеного режиму електричного кола вважатимемо (за умовчуванням), що пройшло достатньо часу й перехідні процеси у колі закінчилися.
Постійні струми та напруга в електричних колах збуджуються джерелами постійного струму та напруги.
Зазначимо, що індуктивність (ідеальний індуктивний елемент) не чинить опору протіканню постійного струму, а ємність (ідеальний ємнісний елемент) взагалі не проводить постійний струм. Тому під час розрахунку електричних кіл постійного струму в якості пасивних елементів розглядаються (як вже було зазначено вище) виключно резистивні елементи.
Розрахунок реакції (аналіз) електричного кола полягає у визначенні струмів крізь всі елементи даного кола та напруги на виводах цих елементів. Процес розрахунку електричного кола нерідко вдається суттєво спростити за рахунок реалізації методу еквівалентних перетворень (методу згортання схеми) заданого електричному колі. При цьому для електричного кола з одним джерелом живлення такі еквівалентні перетворення часто безпосередньо приводять до розв’язання задачі аналізу. Тому метод згортання (еквівалентних перетворень) нерідко визначають як метод розрахунку електричних кіл з одним джерелом живлення.
Метод згортання зазвичай використовується для аналізу нескладних електричних кіл (з одним джерелом живлення, як було вказано) або як складова загального розрахункового алгоритму. Цей метод базується на визначенні еквівалентного опору кола з подальшим використанням законів Ома та Кірхгофа. Під терміном «згортання схеми» розумітимемо заміну окремих ділянок електричного кола їх еквівалентними опорами.
Перетворення послідовно-паралельних з’єднань
Аналіз електричних кіл за методом згортання розглянемо на прикладі кола, наведеного на рис. 3.1.
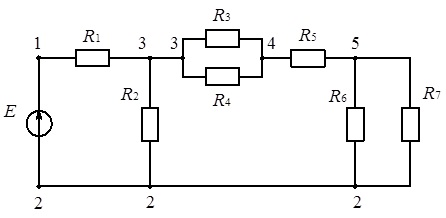
Рис. 3.1. Електричне коло постійного струму (до пояснення методу згортання схеми)
Для визначення еквівалентного опору кола відносно вузлів 1-2, до яких підключене джерело живлення (джерело ЕРС), згортатимемо коло, починаючи з найвіддаленіших від джерела віток.
1. Першим кроком замінюємо паралельно включені опори R6, R7 одним опором R67. Для того, щоб визначити загальний опір двох (або більше) паралельно включених опорів, зазначимо, що паралельне включення резистивних елементів між двома вузлами збільшує електричну провідність між цими вузлами. За таких умов загальна електрична провідність дорівнюватиме сумі електричних провідностей всіх включених паралельно елементів. Так, при паралельному включенні n елементів матимемо
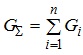 (3.1)
(3.1)
З урахуванням (3.1) сумарний опір паралельно включених елементів R6, R7 визначатиметься як
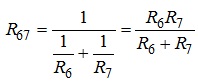
Зазначимо, що, загальний опір паралельного з’єднання визначеної кількості опорів завжди виявляється меншим за найменший з опорів, які утворюють це з’єднання.
Опори R3, R4 також включені паралельно. Отже (за аналогією) записуємо
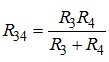 .
.
З урахуванням отриманих результатів щодо перетворення електричного кола, схема якого наведена на рис. 3.1, отримуємо еквівалентне електричне коло (з точки зору опору, приєднаного до затискачів 1-2), схема якого подана на рис. 3.2.
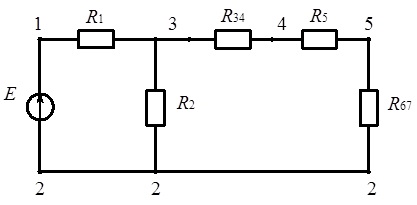
Рис. 3.2. Електричне коло постійного струму (рис. 3.1) після першого етапу перетворення (до пояснення методу згортання схеми)
2. Зі схеми електричного кола (рис. 3.2) видно, що опори R34, R5, R67 включені послідовно, що дозволяє його перетворити на електричне коло, показане на рис. 3.3, врахувавши при цьому, що загальний опір ділянки електричного кола, що містить послідовне з’єднання декількох окремих опорів, дорівнює сумі цих опорів.
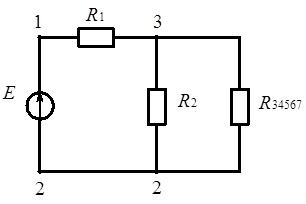
Рис. 3.3. Електричне коло постійного струму (рис. 3.1) після другого етапу перетворення (до пояснення методу згортання схеми)
Тобто
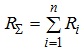 (3.2)
(3.2)
На підставі (3.2)
визначаємо ![]() .
.
Як результат отримуємо електричне коло (див. рис. 3.3), в якому опори R2, R34567 включені паралельно.
3. Паралельне з’єднання опорів R2, R34567 може бути замінене одним опором R234567, котре розраховується як
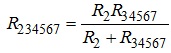 .
.
Таке перетворення приводить до електричного кола, показаного на рис.3.4.
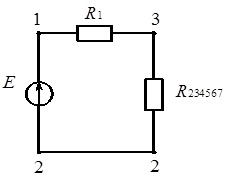
Рис. 3.4. Електричне коло постійного струму (рис. 3.1) після третього етапу перетворення (до пояснення методу згортання схеми)
Зважаючи на те, що після чергового перетворення опори R1, R234567 виявляються включеними послідовно, визначаємо еквівалентний по відношенню до вузлів 1-2 опір наведеного на рис. 3.1 електричного кола як
![]() .
.
Схема електричного кола після реалізації всього комплексу еквівалентних перетворень наведена на рис. 3.5.
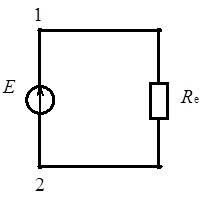
Рис. 3.5. Електричне коло постійного струму (рис. 3.1) після всього комплексу еквівалентних перетворень (до пояснення методу згортання схеми)
Як буде показано надалі, метод еквівалентних перетворень у сукупності з положеннями основних законів електричних кіл постійного струму дозволяє повністю розрахувати електричне коло з одним джерелом живлення.
2. Базові закони електричних кіл постійного струму
Електричні кола постійного струму, що використовуються на практиці, характеризуються великою різноманітністю топології. Відрізняються і цілі, що висуваються в процесі їх аналізу. Все це неминуче призвело до наявності великої кількості різноманітних методів аналізу та розрахунку таких кіл. Однак всі ці методи аналізу базуються на визначених законах, кількість яких відносно невелика. Знання цих законів дозволяє свідомо підходити до вибору методу, який забезпечить найбільшу ефективність як самого процесу аналізу того чи іншого електричного кола, так і використання отриманого результату.
Зазначимо, що як буде показано надалі, з визначеними застереженнями ці закони поширюються і на електричні кола змінного струму, становлять основу методів аналізу й таких електричних кіл.
До таких законів в теорії електричних кіл відносяться закони Ома та Кірхгофа, а також закон суперпозиції (який частіше називають принципом суперпозиції).
2.1. Закон Ома
Закон Ома використовується для розрахунку струмів та напруги на окремих опорах, що утворюють вітку або замкнений контур електричного кола. На рис. 3.6 зображена вітка електричного кола, яка містить n опорів.
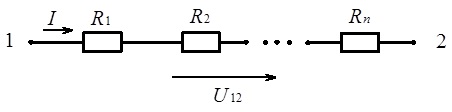
Рис. 3.6. Вітка електричного кола без джерел живлення (до ілюстрації закону Ома)
Напруга між вузлами 1 та 2 вітки, зображеної на рис. 3.6, дорівнює різниці напруги в цих вузлах і розраховується як
![]() .
.
Струм у цій вітці визначатиметься за законом Ома для ділянки електричного кола як
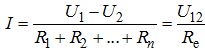 (3.3)
(3.3)
Додатний напрямок струму I у вітці, показаній на рис. 3.6, узгоджений з напрямком напруги U12. На рис. 3.7 зображена вітка електричного кола, яка містить n активних опорів та m джерел живлення (генераторів постійної напруги).
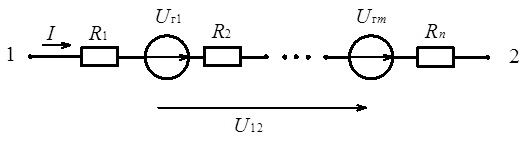
Рис. 3.7. Вітка електричного кола з джерелами живлення (до ілюстрації закону Ома)
Для такої вітки закон Ома матиме вигляд
![]() (3.4)
(3.4)
Зазначимо, що напруги Ur1, ..., Urm джерел живлення записуються в чисельнику (3.4) зі знаком «плюс» за умови, що їх напрямок протилежний напрямку струму у вітці, і зі знаком «мінус» за умови, що вказані напрямки співпадають. При цьому слід пам’ятати, що нами було погоджено позначати напругу на затискачах джерела живлення спрямованою від додатного полюса до від’ємного, тоді як стрілка у позначенні джерела напруги вказує на зростання потенціалу всередині джерела живлення.
Тобто додатну позначку напруги у співвідношенні (3.4) отримуватимемо за умови, що напрямок протікання струму співпадає з напрямком зростання потенціалу всередині джерела живлення. На рис. 3.8 показаний контур електричного кола. Струм у замкненому контурі, зображеному на рис. 3.8, можна знайти за законом Ома для замкненого електричного кола:
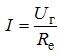 (3.5)
(3.5)
При цьому напрямок струму визначається напрямком напруги джерела живлення. На рис. 3.8 детально показані узгоджені напрямки напруги та струму в електричному колі.
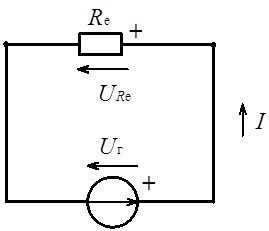
Рис. 3.8. Контур електричного кола до ілюстрації закону Ома
Зверніть увагу, що напруга Ur і напруга URe спрямовані у різні сторони щодо обходу контуру: напрямок напруги Ur відповідає обходу контуру за часовою стрілкою, а напрямок напруги URe відповідає обходу контуру проти часової стрілки. Крім того, додатний напрямок струму у контурі співпадає з напрямком зростання потенціалу всередині джерела живлення, тобто протилежний напрямку напруги на затискачах цього джерела.
Підкреслимо, що визначення узгоджених напрямків напруги та струму слід чітко усвідомлювати, щоб запобігти помилкам, які можуть виникати в процесі аналізу електричних кіл, внаслідок неточностей у встановлені цих напрямків. Для ілюстрації послідовності розрахунків з використанням закону Ома, розглянемо електричне коло, схема якого наведена на рис. 3.9. Наведене коло містить два опори R1, R2, включені паралельно, та джерело постійного струму Ir. Струм I в нерозгалуженій частині наведеного електричного кола дорівнює струму джерела живлення, тобто
![]() .
.
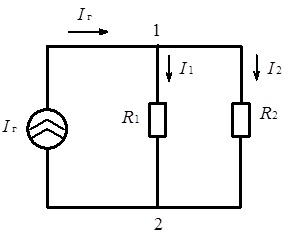
Рис. 3.9. Схема електричного кола до ілюстрації послідовності розрахунків за законом Ома
Для визначення струмів I1, I2 у вітках кола знайдемо напругу U12 між вузлами 1 та 2, використовуючи правило згортання паралельного з’єднання двох опорів і закон Ома. Маємо:
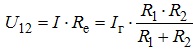 .
.
Надалі неважко розрахувати струм у кожній вітці електричного кола, а саме
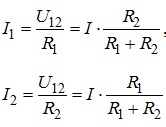
Отримані формули часто називають формулами розкиду або розподілення струму по паралельним віткам електричного кола.
2.2. Закони Кірхгофа
Перший закон Кірхгофа
Перший закон Кірхгофа формулюється як алгебраїчна сума струмів віток, що сходяться в будь-якому вузлі електричного кола, дорівнює нулю.
Математично перший закон Кірхгофа можна подати у вигляді:
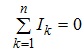 (3.6)
(3.6)
де n - число віток електричного кола, що сходяться у відповідному вузлі.
У співвідношенні (3.6) струми, орієнтація яких однакова відносно вузла, мають бути записані з однаковими знаками. Наприклад, якщо струми, що сходяться до вузла, записуються зі знаком «+», то струми, що розходяться від вузла, слід записати зі знаком «-».
Кількість рівнянь, які під час аналізу електричного кола можна скласти на підставі першого закону Кірхгофа, на одиницю менша за кількість вузлів у цьому колі.
Перший закон Кірхгофа іноді називають законом струмів Кірхгофа. Запишемо, наприклад, рівняння за першим законом Кірхгофа для електричного кола, схема якого наведена на рис. 3.10. Маємо:
для вузла 1
![]() ;
;
для вузла 2
![]() ;
;
для вузла 3
![]() .
.
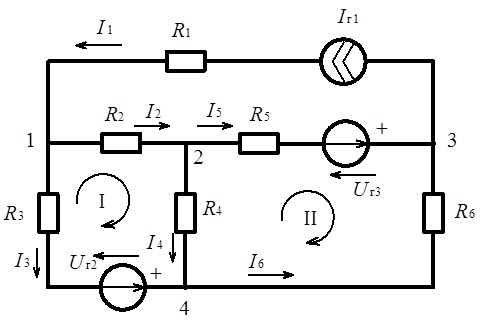
Рис. 3.10. Схема до ілюстрації законів Кірхгофа
Другий закон Кірхгофа
Другий закон Кірхгофа формулюється як алгебраїчна сума напруг віток в будь-якому контурі електричного кола дорівнює нулю.
Математично другий закон Кірхгофа, який також називають законом напруг Кірхгофа, можна подати у вигляді:
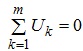 (3.7)
(3.7)
де m - кількість віток, що входять до контуру.
У співвідношенні (3.7) напруги, напрямок яких співпадає з напрямком обходу контуру, слід підставляти зі знаком «плюс», а напруги, напрямок яких не співпадає з напрямком обходу контуру – зі знаком «мінус». Кількість незалежних рівнянь, які можна скласти для визначеного електричного кола за другим законом Кірхгофа, розраховується за формулою:
![]() (3.8)
(3.8)
де nг - загальне число віток електричного кола;
nв - число вузлів електричного кола;
nІдж - число віток електричного кола, які містять джерела струму.
Зазначимо, що для контурів, які містять джерела струму, рівняння за законом напруг Кірхгофа не складають.
Запишемо, наприклад, рівняння за другим законом Кірхгофа для електричного кола, схема якого наведена вище на рис. 3.10. Вибравши напрямок обходу контурів за годинниковою стрілкою, матимемо:
для контуру І
![]() ;
;
для контуру ІІ
![]() .
.
Необхідно проявляти підвищену увагу при встановлені знаків складових у останніх співвідношеннях. Для зручності на рис. 3.10 показані напрямки напруги на затискачах джерел живлення, які, як було роз’яснено вище, протилежні стрілкам всередині джерел живлення, які вказують напрямок підвищення потенціалу.
2.3. Принцип суперпозиції
Принцип суперпозиції, який також називають принципом накладання (або принципом накладання реакцій), можна сформулювати у вигляді: якщо в лінійне електричне коло включені декілька джерел живлення постійного струму або напруги, то реакція кола дорівнюватиме сумі реакцій від кожного джерела окремо.
Цей принцип має силу виключно у лінійних електричних колах, в яких параметри елементів не залежать від рівня струму, що цими елементами протікає, або рівня напруги, яка встановлюється на їх виводах.
Суть цього принципу достатньо прозора і нерідко використовується при аналізі електричних кіл. Особливо за умови, що деякі з усієї сукупності впливів, які діють на елементи електричного кола, змінюються в процесі роботи. Крім того, цей принцип використовується (як основа окремих процедур) в багатьох широковживаних методах розрахунку електричних кіл.
3. Методи розрахунку електричних кіл постійного струму
Розглянуті вище закони покладені в основу цілого ряду методів розрахунку електричних кіл постійного струму. При цьому, як буде показано надалі з визначеними застереженнями ці методи по-більшості можуть бути поширені й на електричні кола синусоїдного струму.
3.1. Метод еквівалентних перетворень
Розглянуті вище еквівалентні перетворення електричних кіл постійного струму у сукупності з законами Ома та Кірхгофа, приводять до методу еквівалентних перетворень, який може ефективно використовуватися при аналізі відносно нескладних електричних кіл (або фрагментів електричних кіл будь-якої складності) з одним джерелом живлення.
Метод еквівалентних перетворень розглянемо на прикладі електричного кола, показаного на рис. 3.1, для якого вже були реалізовані відповідні процедури перетворення схеми, що призвели до її згортання у один опір, приєднаний до затискачів джерела живлення. Для зручності повторимо схему електричного кола на рис. 3.11.
І так, наша мета полягає в розрахунку струмів, що протікають крізь елементи кола, на підставі методу еквівалентних перетворень з використанням законів Ома та Кірхгофа. Вибираємо напрямки струмів у вітках електричного кола так, як це подано на рис. 3.11. Нагадаємо, що цей вибір може бути, взагалі кажучи, довільний, але ми будемо дотримуватися вже прийнятих й апробованих правил.
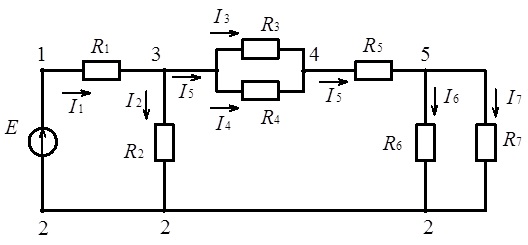
Рис. 3.11. Схема електричного кола до розрахунку реакцій на підставі методу згортання з використанням законів Ома та Кірхгофа.
Вище відповідними еквівалентними перетвореннями було визначено значення еквівалентного опору Re наведеного електричного кола по відношенню до затискачів джерела напруги (E=Uг), а саме було отримане співвідношення:
На підставі закону Ома розраховуємо струм I1:
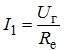 .
.
Струм I2 знаходимо за формулою розкиду струму по паралельним віткам, зважаючи на те, що опори R2, R34567 включені паралельно. Маємо:
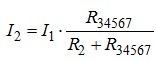 .
.
Струм І5 можна знайти за формулою розкиду струмів або за законом струмів Кірхгофа для вузла 3.
Вибравши закон струмів Кірхгофа, матимемо:
![]() .
.
Значення струмів І3, І4, І6, І7 знаходимо за формулами розкиду струмів, а саме:
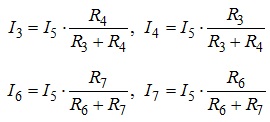
Зазначимо, що для визначення струмів І4, І7 можна також використати рівняння, складені за законом струмів Кірхгофа для вузлів 4 та 5, а саме:
![]() .
.
Таким чином, нами розраховані за допомогою еквівалентних перетворень схеми та законів Ома й Кірхгофа струми у всіх вітках електричного кола постійного струму з одним джерелом живлення (джерелом постійної напруги). При необхідності за законом Ома можна розрахувати напругу між будь-якими двома вузлами даного електричного кола.
Наприклад, для визначення напруги (U32) між вузлами 3 та 2, можна скористатися будь-якою з формул:
![]() .
.
3.2. Метод струмів віток
Метод струмів віток базується на рівняннях, складених для заданого електричного кола за законами Кірхгофа. З усіх рівнянь, які можна отримати за такий спосіб, відбирають незалежні. Ці незалежні рівняння об’єднують в систему, розв’язання якої дає значення струмів у вітках електричного кола. Реалізацію методу струмів розглянемо на конкретному прикладі електричного кола, схема якого наведена на рис. 3.12.
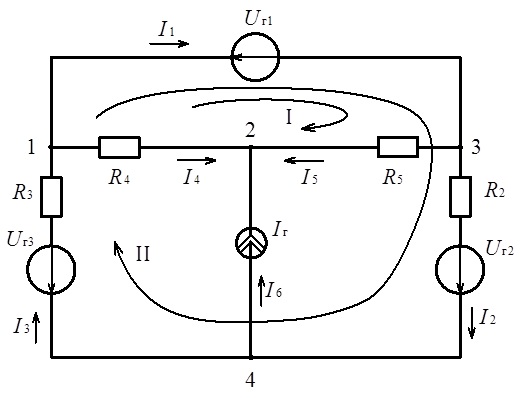
Рис. 3.12. Схема електричного кола до ілюстрації методу струмів віток
Наведена схема містить чотири вузла. Це означає, що за законом струмів Кірхгофа можна скласти три незалежних рівняння. За законом напруг Кірхгофа кількість незалежних рівнянь становитиме:
![]() .
.
Отже для наведеного електричного кола усього за законами Кірхгофа можна скласти п’ять незалежних рівнянь.
Складаємо рівняння для вузлів 1, 2, 3, а також для двох контурів: верхнього контуру І та зовнішнього контуру ІІ. При цьому, як видно, контур ІІ не включає джерело струму Іг.
Зазначимо, що незалежні контури у схемі вибрані таким чином, щоб жоден з них не містив вітку з джерелом струму. Це пов’язане з тим, що струм у контурі з джерелом струму визначатиметься параметрами (струмом) виключно цього джерела, тобто не міститиме ніякої додаткової інформації, щодо розподілення напруги на виводах елементів такого контуру. Інформаційною за таких умов буде напруга, що діє на затискачах цього джерела, яка є додатковою невідомою величиною, що потребуватиме складання ще одного рівняння.
Вибираємо напрямок обходу кожного контуру за годинниковою стрілкою.
Як результат отримуємо систему з п’яти рівнянь з п’ятьма невідомими струмами віток:
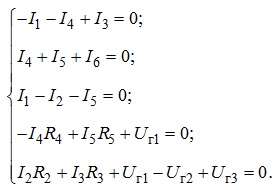
Ще раз звернемо увагу на позначки при елементах наведених рівнянь. Підкреслимо той факт, що позначка при елементі, що відображає джерело напруги є додатною, за умови, що напрямок обходу контуру співпадає з напрямком відповідної напруги, тобто з напрямком зменшення потенціалу на зовнішніх затискачах джерела (див. Uг1, Uг3 у четвертому та п’ятому рівняннях). В протилежному випадку позначка при відповідному елементі буде від’ємною (див. Uг2 у п’ятому рівнянні).
Знову ж нагадаємо, що стрілка у зображенні джерела напруги вказує на підвищення потенціалу всередині джерела, тобто спрямована у бік, протилежний напрямку напруги на затискачах цього джерела.
Розв’язання вказаної системи й визначає шукані струми у всіх елементах схеми. За необхідністю на підставі закону Ома можна отримати й величину напруги на кожному з елементів заданого кола.
При розрахунку реакції складних лінійних електричних кіл кількість рівнянь, що складаються за законами Кірхгофа, буває надто великою, а отже й розв’язання відповідних систем лінійно-незалежних рівнянь стикається з суттєвими труднощами обчислювального характеру. Тому були розроблені інші економніші з точки зору обчислювальних витрат методи розрахунку електричних кіл, при використанні яких закони Кірхгофа використовуються як основа методу та для реалізації процедур перевірки правильності отриманих результатів.
3.3. Метод контурних струмів
Метод контурних струмів заснований на другому законі Кірхгофа. Цей метод дозволяє зменшити кількість рівнянь у системі до:
![]() .
.
Порядок розрахунку струмів у вітках електричного кола за методом контурних струмів можна подати наступним алгоритмом:
- Вибираємо (довільно) напрямки струмів у вітках.
- Вибираємо незалежні контури, й задаємо напрямки умовних струмів, які звуться контурними струмами.
- Для кожного з вибраних контурів складаємо систему лінійних незалежних рівнянь за другим законом Кірхгофа. Розв’язання цієї системи дозволяє знайти всі контурні струми.
- Визначаємо струми у вітках заданого електричного кола як алгебраїчну суму контурних струмів, що протікають відповідними вітками.
Розглянемо використання методу контурних струмів на прикладі розрахунку електричного кола, схема якого надана на рис. 3.13.
Довільно вибираємо напрямки струмів у вітках (див. рис. 3.13). Наведена схема містить три контри (І, ІІ, ІІІ). Вибираємо напрямки контурних струмів (Ік1, Ік2, Ік3) за часовою стрілкою. З наведеного рис. 3.13 видно, що контуром ІІІ замикається струм джерела живлення, тобто контурний струм третього контуру Ік3 визначається виключно струмом цього джерела. Отже безпосередньо маємо:
![]() .
.
Таким чином для формування системи незалежних рівнянь використовуємо лише два контури (І та ІІ). Правило складання рівнянь засноване на тому, що кожен контурний струм створює у відповідному контурі відповідне розподілення напруги.
Вказане розподілення пов’язане з (визначається):
- даним контурним струмом та всіма опорами, які входять до цього контуру; ці напруги звуться власними напругами;
- суміжними контурними струмами та опорами віток, які є суміжними між відповідними контурами; ці напруги звуться взаємними напругами.
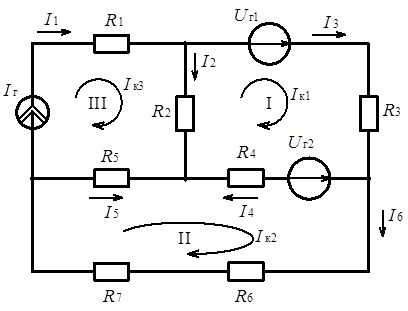
Рис. 3.13. Схема електричного кола до ілюстрації методу контурних струмів
Для схеми, наведеної на рис. 3.13 контурний струм Ік1 створює в першому контурі власну напругу:
![]() ,
,
а контурні струми Ік2, Ік3 внесуть до цього ж контуру взаємні напруги:
![]() .
.
Знак «мінус» в останніх виразах означає, що контурний струм першого контуру й контурні струми інших контурів направлені протилежно один одному.
Аналогічно власна напруга, що утворюється струмом Ік2 у другому контурі, дорівнюватиме:
![]() ,
,
Взаємні напруги, які утворюються контурними струмами сусідніх (першим та третім) контурів, дорівнюватимуть:
![]() .
.
За другим законом Кірхгофа алгебраїчна сума всіх внесених у контур напруг має дорівнювати нулю. Отже кінцева система рівнянь для електричного кола, що розглядається, матиме вигляд:
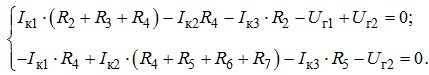
Під час використання методу контурних струмів зазвичай використовують канонічну форму запису такої системи рівнянь. При цьому вводять поняття:
- власний опір контуру, який є сумою опорів всіх віток, що утворюють даний контур (в загальному випадку цей опір позначається як Rii, де і – номер контуру);
- взаємний опір контуру, який є загальним опором для даного та сусіднього контурів (в загальному випадку цей опір позначається як Rii, де i, j – номери даного та сусіднього контуру відповідно);
- контурна напруга джерел, яка є алгебраїчною сумою напруги всіх джерел, що входять до даного контуру (цю напругу позначатимемо як Uкі, де і – номер контуру).
З урахуванням наведеного маємо:
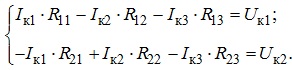 (3.9)
(3.9)
В наведених у (3.9) рівняннях використані позначення:
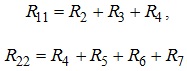
які відображають власні опори першого та другого контурів;
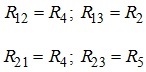
які відображають взаємні опори між відповідними контурами;
![]() ,
,
які відображають сумарні напруги джерел живлення, що діють в першому та другому контурі відповідно.
Під час складання системи рівнянь (3.9) користуються визначеними правилами встановлення знаків при елементах рівнянь, а саме:
- власний опір завжди має знак «плюс»;
- взаємному опору надається знак «плюс» за умови, що контурні струми відповідних суміжних контурів протікають крізь нього в одному напрямку, та знак «мінус» за умови, що вказані контурні струми протікають крізь взаємний опір в протилежних напрямках;
- напрузі джерела живлення, записаній в правій частині рівнянь, надається знак «плюс» за умови, що напрямок цієї напруги протилежний напрямку відповідного контурного струму (тобто за умови, що напрямок контурного струму співпадає з вказаним стрілкою напрямком збільшення потенціалу всередині даного джерела живлення), і знак «мінус» за умови, що напрямок вказаної напруги співпадає з напрямком відповідного контурного струму (тобто за умови, що напрямок контурного струму протилежний вказаному стрілкою напрямку збільшення потенціалу всередині даного джерела живлення).
В загальному випадку, коли електричне коло постійного струму містить т незалежних контурів, система рівнянь у канонічній формі матиме вигляд:
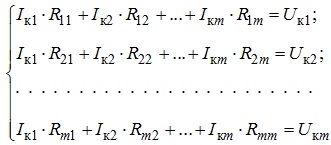 (3.10)
(3.10)
З системи лінійних рівнянь (3.10), використовуючи відомі правила та алгоритми, знаходять контурні струми Ік1, Ік2, …, Ікт. Для розглянутого вище прикладу з системи рівнянь (3.10) знайдемо контурні струми Ік1, Ік2, використовуючи правило Крамера:
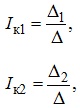
де 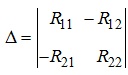 - головний визначник
системи (3.10);
- головний визначник
системи (3.10);
Δ1, Δ2 - визначники, які отримані шляхом заміни в головному визначнику (Δ) першого або другого стовпця відповідно на стовпець вільних членів, а саме:
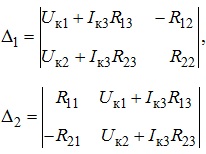
На підставі розрахованих контурних струмів неважко знайти струми у вітках, використовуючи принцип суперпозиції. При цьому враховуємо правило: якщо напрямок контурного струму співпадає з напрямком струму у вітці, то останній береться зі знаком «плюс», якщо ж вказаного співпадіння немає, то зі знаком «мінус».
З урахуванням наведеного, для електричного кола, поданого на рис. 3.13, отримуємо:
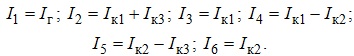
При використанні методу контурних струмів слід враховувати, що за умови наявності в електричному колі віток з джерелами струму, незалежні контури слід вибирати так, щоб такі вітки до них не входили. Для врахування дії цих джерел їх струми замикаються через вітки, що не містять інших джерел струму.
3.4. Метод вузлових потенціалів
Метод вузлових потенціалів (вузлових напруг) заснований на законі струмів Кірхгофа та законі Ома. Цей метод дозволяє зменшити кількість рівнянь в системі до (nв-1).
Алгоритм реалізації методу вузлових потенціалів можна подати у вигляді:
- Довільно вибираємо напрямки струмів у вітках.
- Заземлюємо один з вузлів, завдяки чому його потенціал стає рівним нулю. Цей вузол зазвичай називають базисним вузлом.
- Складаємо систему лінійних незалежних рівнянь для вузлів електричного кола за законом струмів Кірхгофа. Розв’язання цієї системи рівнянь дозволяє знайти потенціалі вузлів, а в подальшому й напруги (різниці потенціалів) між вказаними вузлами.
- Використовуючи закон Ома для ділянки кола, знаходимо струми у вітках заданого кола.
Розглянемо використання методу вузлових потенціалів для розрахунку кола, аналогічного тому, яке використовувалося під час розгляду методу контурних струмів. Для зручності це коло наведене на рис. 3.14 з позначками, необхідними для реалізації алгоритму методу вузлових потенціалів.
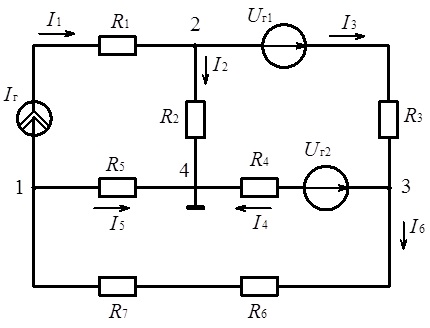
Рис. 3.14. Схема до ілюстрації методу вузлових потенціалів
Напрямки струмів у вітках вибираємо довільно.
Заземлюємо вузол 4, тим самим роблячи його базисним. Це означатиме, що потенціал цього вузла дорівнюватиме нулю (V4=0).
Для вузлів 1, 2, 3 складаємо систему лінійних незалежних рівнянь за законом струмів Кірхгофа, тобто враховуючи, що алгебраїчна сума струмів у кожному вузлі має дорівнювати нулю.
За вказаних умов у вузлі 1 зійдуться струми:
- вузловий струм, який утворюється джерелом напруги або струму (в даному випадку це струм - Іг, який витікає з вузла 1);
- власний струм вузла, який визначається потенціалом першого вузла та провідностями всіх віток, що у цьому вузлі сходяться, а саме
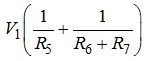 ;
;
- взаємні струми вузла, які визначаються потенціалами суміжних вузлів та провідностями відповідних віток, що зв’язують ці вузли з вибраним (вузлом 1), а саме:
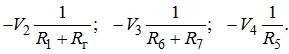
Нагадаємо, що внутрішній опір джерела струму Rг спрямовується до нескінченності, тому провідність відповідної вітки дорівнює нулю; дорівнює нулю й потенціал V4 вузла 4. Тобто серед взаємних струмів вузла 1 ненульовим виявляється лише струм, що зв’язує перший і вузол. Зазначимо, що взаємні струми вузла завжди беруться зі знаком «мінус», а знак вузлового струму залежить від того, втікає цей струм у вузол чи витікає з нього. Вузловий струм, який утворюється джерелом напруги (див., наприклад, вузол 2), визначається відношенням напруги цього джерела до опору вітки, в яку це джерело увімкнене. Проводячи для вузлів 2 та 3 аналогічні міркування, отримуємо систему рівнянь вузлових потенціалів для заданої схеми, а саме:
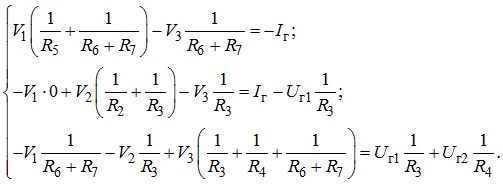
В канонічній формі запису наведена система рівнянь матиме вигляд:
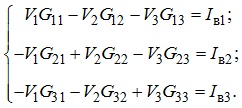
В останній системі рівнянь використані позначення:
- потенціали вузлів 1, 2, 3 електричного кола:
![]() ;
;
- власні провідності:
вузла 1 (G11),
вузла 2 (G22),
вузла 3 (G33),
які дорівнюють сумі провідностей всіх віток, що приєднані до кожного вказаного вузла, визначаються як:
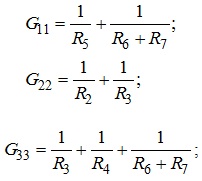
- взаємні провідності:
вузла 1 та вузла 2 (G12 = G21),
вузла 1 та вузла 3 (G13 = G31),
вузла та вузла 3 (G23 = G32),
які дорівнюють сумі провідностей всіх віток, що включені між відповідною парою вузлів, визначаються як:
![]()
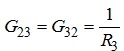 ;
;
- задавальні вузлові струми
вузлів 1 (Із1),
вузла 2 (Із2),
вузла 3 (Із3),
які дорівнюють алгебраїчній сумі струмів всіх джерел, підключених до кожного з вузлів, визначаються як:
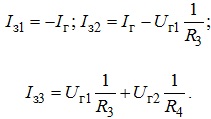
Під час складання рівнянь вузлових потенціалів необхідно користуватися наступним «правилом знаків»:
- власні провідності завжди беруться зі знаком «плюс»,
- взаємні провідності завжди беруться зі знаком «мінус»,
- задавальні струми джерел беруться зі знаком «плюс», якщо ці струми направлені до вузла, і зі знаком «мінус», якщо ці струми направлені від вузла.
За умови, що резистивне електричне коло містить п вузлів, отримуємо узагальнену систему рівнянь в канонічній формі. За умови, що заземлено п-й вузол, тобто (Vп=0), матимемо:
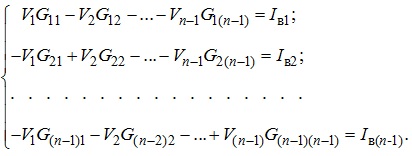 (3.11)
(3.11)
З системи лінійних рівнянь (3.11) знаходимо потенціали вузлів:
![]() ,
,
використовуючи, наприклад, правило Крамера.
Для прикладу, що розглядався вище, зі сформованої системи рівнянь для кола, наведеного на рис. 3.14, за правилом Крамера потенціали вузлів 1, 2 та 3 знаходимо як:
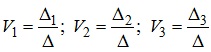
де Δ - головний визначник системи, який розраховується як:
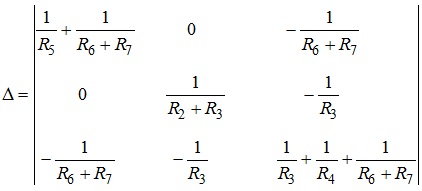
Визначники Δ1, Δ2, Δ3 отримуємо, замінюючи в головному визначнику відповідний стовпець на стовпець задавальних вузлових струмів. Надалі, знаючи потенціали вузлів, знаходимо струми у вітках кола, використовуючи закон Ома. Маємо:
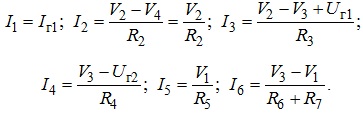 .
.
Під час використання методу вузлових потенціалів слід пам’ятати, що за наявності у колі вітки, яка містить виключно ідеальне джерело напруги, як базисний вибирають один з вузлів, до яких приєднана ця вітка. При цьому потенціал другого вузла виявляється одразу відомим, адже він дорівнюватиме напрузі вказаного джерела взятому зі знаком «плюс» або «мінус» в залежності від полярності цього джерела. Рівняння за методом вузлових потенціалів для такого вузла складати не треба, але його потенціал враховується при складанні рівнянь для інших вузлів.
Струм у вітці з ідеальним джерелом напруги не можна розраховувати, використовуючи закон Ома, адже опір такого джерела дорівнює нулю. Тому для розрахунку струмів у таких вітках використовують закон струмів Кірхгофа після розрахунку струмів у всіх інших вітках електричного кола.
4. Методика контролю розрахунків електричних кіл постійного струму
Під час розрахунку електричних кіл з великою кількістю елементів, актуальною стає задача оперативної перевірки правильності отриманого результату. З цією метою розроблено спеціальні процедури, реалізація яких дозволяє надати відповідь на питання щодо правильності результату. До таких процедур відносяться:
- перевірка балансу потужності в електричному колі;
- побудова потенціальної діаграми.
4.1. Баланс потужності в електричному колі постійного струму
Під балансом потужності електричного кола розуміємо тотожність потужності всіх джерел електричної енергії, що діють в даному електричному колі, і потужності, що розсіюється на всіх елементах цього кола. Математично це можна подати як:
![]()
де ![]() -
сумарна потужність всіх джерел ЕРС, що діють в електричному колі;
-
сумарна потужність всіх джерел ЕРС, що діють в електричному колі;
![]() -
сумарна потужність, що розсіюється на елементах електричного кола.
-
сумарна потужність, що розсіюється на елементах електричного кола.
Як видно з наведених співвідношень, потужність, що розсіюється на будь-якому елементі електричного кола завжди є величиною додатною. Це й зрозуміло, адже елементами електричного кола постійного струму здійснюється перетворення енергії електричного струму на теплову енергію (односторонній процес).
В той же час, потужність джерела живлення, що діє в даному електричному колі може мати як додатну, так і від’ємну позначку. Це обумовлене взаємним спрямуванням струму Ij і напруги Ui. Узгоджений напрямок струму й напруги дає додатну позначку відповідного добутку й означатиме, що дане джерело живлення віддає енергію в електричне коло, тоді як неузгоджений напрямок дає від’ємну позначку відповідного добутку й означатиме, що дане джерело живлення генерує енергію, яка протидіє енергії електричного струму (який спричиняється іншими джерелами живлення даного кола) в даному місці електричного кола.
4.2. Потенціальна діаграма
Потенціальна діаграма являє собою графічне подання розподілення електричного потенціалу вздовж вибраного шляху на схемі електричного кола.
Побудова потенціальної діаграми визначеного електричного кола з відомими параметрами всіх його складових відбувається за наступним алгоритмом:
- Розраховуємо струми, що протікають елементами кола.
- Прийнявши потенціал однієї з точок схеми за первісний розраховуємо потенціали у всіх інших точках. Первісний потенціал може бути вибраний довільної величини, хоча по-більшості його вважають нульовим.
- Будуємо потенціальну діаграму, подаючи зміни потенціалу вздовж кола на графіку в координатах потенціалу φ та опору R.
Реалізацію наведеного алгоритму проілюструємо на прикладі побудови потенціальної діаграми для контуру електричного кола, схема якого наведена на рис. 3.15. Вважаючи, що для наведеного на рис. 3.15 контуру електричного кола, відомі потенціал точки А та струми, що протікають елементами кола, розрахуємо потенціали у точках:
![]() ,
,
а також потенціал точки А, як кінцевої точки розрахунку:
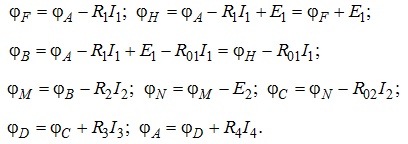
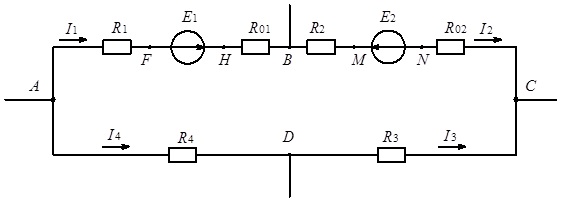
Рис. 3.15. Схема контуру електричного кола до ілюстрації побудови потенціальної діаграми
Зазначимо, що розрахунок потенціалу φА є перевіркою правильності розрахунку інших потенціалів, адже отримане значення цього потенціалу має співпадати з первісно прийнятим значенням. Будуємо потенціальну діаграму за розрахованими даними (див. рис. 3.16).
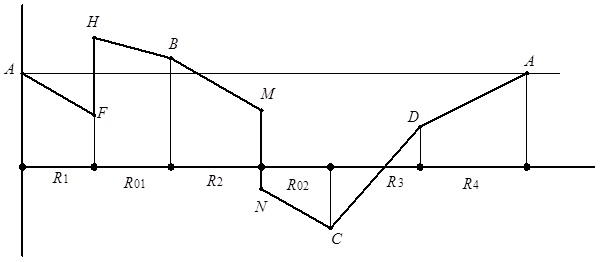
Рис. 3.16. Потенціальна діаграма контуру, наведеного на рис. 3.15
На осі абсцис (вісь опорів R) у вибраному масштабі відкладаємо значення опорів:
![]() .
.
На осі ординат (вісь потенціалів φ) відкладаємо значення потенціалу точки A.
Задаємо обхід контуру за годинниковою стрілкою.
Перехід від точки A до точки F супроводжується падінням потенціалу на величину I1R1, що приводить до точки F діаграми.
Переходячи через джерело напруги, потенціал змінюється стрибком, а саме, збільшується на величину E1, адже джерело генерує напругу, напрямок якої співпадає з вибраним напрямком обходу контуру.
Надалі, аналогічно, переходимо від однієї точки схеми до іншої.
Зазначимо, що при переході через джерело напруги E2 потенціал стрибкоподібно спадає, адже це джерело вносить у коло напругу, напрямок якої протилежний напрямку обходу контуру.
При переході від точки C до точки D і далі до точки A потенціал зростатиме, бо напрямок обходу контуру виявляється на цій ділянці кола протилежним напрямку струму крізь відповідні елементи (R3, R4).
Потенціал кінцевої точки діаграми, звичайно, має співпадати з початковою, адже наведене коло являє собою замкнений контур.
Потенціальна діаграма графічно відображає другий закон Кірхгофа.
Дійсно, відповідно до наведених рівнянь, можна записати:
![]() ,
,
що співпадає з записом другого закону Кірхгофа для контуру, який розглядається.
Зазначимо, що тангенс кута нахилу будь-якої лінії графіка до осі абсцис пропорційний значенню струму у відповідному місці контуру.
5. Презентація до лекції 3
Для завантаження натисніть сюди: "Презентація до лекції 3".
Шрифти
Розмір шрифта
Колір тексту
Колір тла
Кернінг шрифтів
Видимість картинок
Інтервал між літерами
Висота рядка
Виділити посилання
Text Alignment