Тема 2. Ідеалізація об’єкта при створенні комп’ютерної моделі. Ідеалізація форми й геометричних параметрів конструкції.
| Сайт: | Навчально-інформаційний портал НУБіП України |
| Курс: | Основи автоматизованого проектування в будівництві ☑️ |
| Книга: | Тема 2. Ідеалізація об’єкта при створенні комп’ютерної моделі. Ідеалізація форми й геометричних параметрів конструкції. |
| Надруковано: | Гість-користувач |
| Дата: | середа, 17 грудня 2025, 02:40 |
1. Роль розрахункових САПР у вирішенні задач будівельної механіки
Будь-яка інженерна споруда - будівля, міст, тунель, автомобіль, корабель та ін. - крім елементів, забезпечують функціональне призначення даного об'єкта, обов'язково має несучі елементи конструкції, що становлять «силовий каркас» і призначені для сприйняття навантажень і різних силових впливів на конструкцію. Часто функціональні і несучі властивості поєднуються, наприклад, стіни і перекриття будівлі виконують огороджувальні функції і одночасно входять до складу несучої частини конструкції.Несучі елементи конструкції повинні проектуватися і створюватися так, щоб вони були міцними, тобто могли сприймати всі силові дії, не руйнуючись протягом досить тривалого часу. Коротко кажучи, конструкції повинні бути міцними і довговічними.
Несуча конструкція, наприклад пролітна конструкція моста, може бути досить міцною, але надмірно деформативною, недостатньо жорсткою. Як наслідок, в конструкції можуть виникати коливання, що ускладнюють або навіть роблять неможливою її експлуатацію.
Сильно стиснута, але недостатньо жорстка колона може зігнутися (випучитися) від дії стискаючого навантаження, що пов'язане з так званим явищем втрати стійкості колони.
Проблемами розрахунку різних типів споруд і їх несучих конструкцій на міцність, жорсткість і стійкість займається інженерна наука - будівельна механіка. Сучасні розрахункові програмні комплекси (напряму CAD або САПР), за допомогою методу скінченних елементів, на базі якого базуються їх розрахункові процесори, дозволяють вирішувати задачі будівельної механіки проектування будівельних об'єктів із оптимальними швидкістю та достовірністю.
2. Ідеалізація об’єкта при створенні комп’ютерної моделі
Побудова розрахункової комп’ютерної моделі, як і розрахункової схеми в будівельній механіці, починається з ідеалізації конструкції. Цей етап настільки звичний і природний для інженера, що, як правило, виконується підсвідомо, хоча корисно знову осмислити виконувані дії.
Під час створення розрахункової схеми складної конструкції зазвичай вдаються до певної ідеалізації її форми, при цьому ступінь цієї ідеалізації впливає на достовірність результатів розрахунку. Моделювання геометричної форми проводиться на основі геометричних міркувань («схожості» форми) і починається з виділення з об’єкта його несучої частини. І якщо в каркасному будинку достатньо просто вказати на його основні несучі конструктивні елементи, то для будівель із несучими стінами (цегляними або залізобетонними) це вдається зробити не одразу.
Отже, несучі елементи в таких будівлях можуть виявитися різними для різних режимів роботи.
Реальний об’єкт замінюється ідеалізованим деформованим тілом, яке моделює його найважливіші властивості. Основними елементами розрахункових схем є стержень (балка), плоска стіна, деформована у своїй площині, (що перебуває в плоскому напруженому стані), згинальна пластина, просторове масивне тіло, яке перебуває у тривимірному напруженому стані, двовимірне масивне тіло, що перебуває в плоскому деформованому стані. Розрахункова модель-схема - це ідеалізований об’єкт, позбавлений неістотних для результатів розрахунку ознак. Вона передбачає ідеалізацію:
- форми й геометричних параметрів об’єкта;
- умов обпирання та вузлових з’єднань;
- фізичних властивостей матеріалів;
- навантажень і впливів на об’єкт;

а) б)

в)
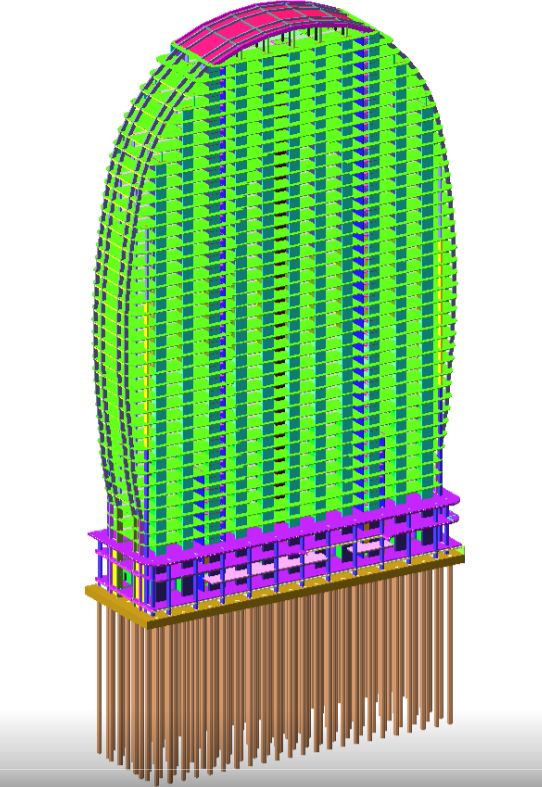
Рис. 2.1 41- поверховий багатофункціональний комплекс в м. Батумі, Грузія.
Архітектурна (віртуальна) модель (а), розрахункова схема в ПК "ЛІРА САПР" (б) та його будівництво (в)
3. Ідеалізація форми й геометричних параметрів конструкції
Ідеалізація геометричних параметрів - призначення основних розмірів, які можуть дещо відрізнятися від реальних з метою надання можливої регулярності для скорочення обсягу вихідної інформації та зручності аналізу результатів. У разі прийняття стержневої або пластинчастої схеми відбувається заміна стержнів на «дротову» систему, а пластин — на площинну, яка не має поперечних розмірів. Тут також можливі відступи, допустимість яких визначає інженер: прийняті осі стержнів і пластин можуть не збігатися з їх нейтральними площинами, різні конструктивні включення (наприклад, консолі) можуть бути проігноровані та ін.
Після того, як обрана та частина об’єкта, що фігуруватиме в розрахунку, починається ідеалізація її геометричного образу - геометричне моделювання. У процесі геометричного моделювання вирішується питання про можливу ідеалізацію об’єкта щодо надання йому властивостей регулярності або симетрії [2], хоча сам об’єкт, можливо, і не є строго регулярним, а умови симетрії можуть бути певною мірою порушені.
Основними геометричними схемами елементів конструкцій є: стержень, плита, оболонка, масивне тіло (рис. 2.2).
Стержень — тіло, довжина якого набагато більша від розмірів перерізу, тобто l > h, b.
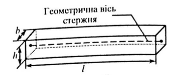
Рис. 2.1 Загальний вигляд стержня
Переважна робота матеріалу в стержні - це розтяг або стиск в осьовому напрямку (особливість представляє деформація кручення). Для фізико-математичної моделі стержня характерним є те, що основні розрахункові рівняння записуються щодо однієї незалежної змінної - координати z. Їх рішення становить так звану одновимірну задачу.

Рис. 2.2 Деформація стержневого елемента
Поперечний переріз — переріз, що лежить у площині, ортогональній геометричній осі.
Пластина – тіло, товщина якого набагато менша від довжини й висоти, тобто δ < b,l.
Природно викривлена пластина (криволінійна до завантаження) називається оболонкою.
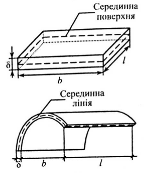
Рис. 2.3 Загальний вигляд пластини і оболонки
Матеріал пластин і оболонок працює в більш складних умовах, ніж у стержня, наприклад, на розтяг - стиск він буде працювати в двох взаємно перпендикулярних напрямках. Математична модель пластин і оболонок, як правило, буде складатися з рівнянь, що залежать від двох аргументів: х та у. Тому така задача відноситься до класу двовимірних задач.
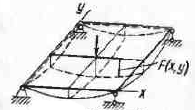
Рис. 2.4 Деформування пластини
Масивне тіло – тіло, у якого всі розміри порівнянні, тобто h-b-l.
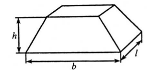
Рис. 2.5 Загальний вигляд масивного тіла
Зважаючи на відсутність будь-якого переважного напрямку в тілі функції, що описують його деформування, будуть істотно залежати від трьох незалежних аргументів х, у, z, тому задача є тривимірною.
Геометрично ці елементи відрізняються один від одного лише співвідношенням характерних розмірів, але з механічної точки зору їх деформування є настільки специфічним, що вимагає отримання своїх рівнянь і залежностей, які складають математичну модель цих елементів.
Стержневі елементів в залежності від їх призначення і виду деформування (рис. 2.6) поділяються на:
- Балки (стержні або бруси, які в основному працюють на згин);
- Стійки або колони (стержневі елементи, що сприймають вертикальні стискаючі сили);
- Розкоси (похилі елементи, що сприймають вертикальні стискаючі сили);
- Вали (стержень, що передає обертальний рух, наприклад, від двигуна до верстата).
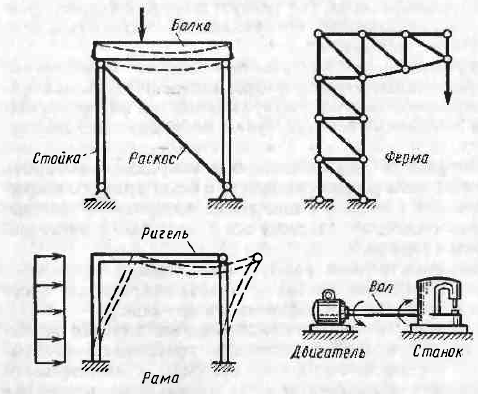
Рис. 2.6 Види стержневих конструкцій
Конструкцію, що складається із сполучених згинальних стержнів, називають рамою. Якщо ж завдяки шарнірному з'єднанню стержнів всі вони працюють тільки на розтяг або стиск (від навантаження, прикладеного у вузлах), то конструкцію називають фермою.
Посилання на додаткове відео стосовно розглянутої теми - тема https://fex.net/uk/s/mycmon5
Шрифти
Розмір шрифта
Колір тексту
Колір тла
Кернінг шрифтів
Видимість картинок
Інтервал між літерами
Висота рядка
Виділити посилання
Text Alignment