Лекція 4. Електричні кола однофазного синусоїдного струму
| Сайт: | Навчально-інформаційний портал НУБіП України |
| Курс: | Електротехніка в будівництві ☑️ |
| Книга: | Лекція 4. Електричні кола однофазного синусоїдного струму |
| Надруковано: | Гість-користувач |
| Дата: | середа, 12 листопада 2025, 20:22 |
Зміст
- 1. Основні визначення та форми відображення синусоїдних величин
- 2. Елементи електричних кіл синусоїдного струму та їх властивості
- 3. Послідовне з’єднання елементів в електричному колі синусоїдного струму
- 4. Електричні кола синусоїдного струму з паралельним з’єднанням елементів
- 5. Презентація до лекції 4
1. Основні визначення та форми відображення синусоїдних величин
Як вже було зазначено, існування електричного струму нерозривно пов’язане з існуванням електричного і магнітного полів. При змінному струмі ці поля змінюються у часі. Магнітне поле, що змінюється у часі, наводить у провідниках ЕРС. Електричне поле, що змінюється у часі супроводжується зміненням величини заряду, наведеного цим полем на провідниках. У провідниках, а частково і в оточуючому середовищі електромагнітна енергія перетворюється на теплову. Деяка частка енергії електромагнітного поля випромінюється. Описані явища відбуваються на всіх ділянках електричного кола, яким протікає змінний електричний струм.
На практиці для спрощення аналізу реальне електричне коло змінного струму замінюють еквівалентною схемою заміщення, елементи якої ідеалізовані. Це дозволяє розподілити вказані процеси між елементами електричного кола змінного струму, суттєво спростивши задачі дослідження й розрахунку таких кіл. Електричні величини (струми, напруги, ЕРС), які змінюються в часі за величиною та напрямком називаються змінними величинами. Один з можливих напрямків змінної електричної величини приймають як додатний напрямок.
Електрична величина вважається цілком визначеною за умови, що відома її залежність від часу, тобто відома відповідна функція f(t) та вказано додатний напрямок цієї величини.
Значення, які набувають змінні електричні величини кожної миті часу, називаються миттєвими значеннями. Для позначення миттєвих значень струмів, напруг та ЕРС зазвичай вживають малі літери латинського алфавіту, наприклад, i, u, e. Величини, миттєві значення яких повторюються через визначені однакові проміжки часу, називають періодичними, а найменший проміжок часу, через які ці повторення відбуваються, називають періодом, який зазвичай позначають як Т. Таким чином, наприклад, миттєве значення періодичного струму в кожному циклі повторення дорівнюватиме:
![]() .
.
Величина, обернена періоду відповідної змінної величини, називається циклічною частотою f цієї величини (зазвичай слово «циклічна» опускають). Отже:
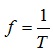 .
.
Циклічна частота вимірюється в герцах (Гц).
При частоті 1 Гц період Т=1 с, тобто 1 Гц = 1 с-1.
Приклад періодичного струму наведений на рис. 4.1. Зазначимо, що постійний струм можна розглядати, як такий окремий випадок періодичного струму, для якого період Т є нескінченно великим. При цьому, звичайно, циклічна частота дорівнюватиме нулю, тобто:
![]()
Крім циклічної частоти поширення отримала величина ω, що визначається як:
![]() .
.
Ця величина зветься кутовою або круговою частотою і вимірюється в рад/с. Зміст цієї величини обговорюватимемо надалі.
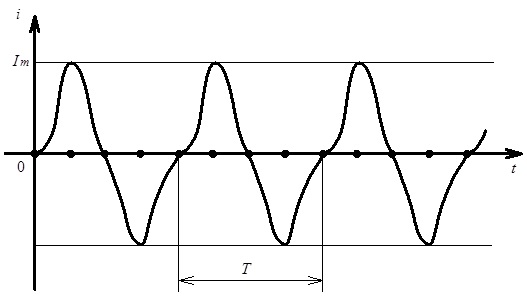
Рис. 4.1. Приклад періодичного струму Т - період; Іт - амплітудне значення
Найбільше з миттєвих значень електричних величин, що періодично змінюються, зветься максимальним або амплітудним значенням (амплітудою). Найбільш поширені найпростіші гармонічні або синусоїдні електричні величини (струми, напруги, ЕРС). За умови, що електричне коло лінійне, при синусоїдній ЕРС струми та напруги також синусоїдні. В енергетичних системах більшості країн світу (в т.ч. в країнах бувшого СРСР та Європи прийнята стандартна частота синусоїдного струму 50 Гц. В США – 60 Гц. Взагалі кажучи на сьогодні в різних за призначенням системах знаходять застосування електричні коливання від долів герца до мільярдів герц. Аналітичний запис синусоїдної величини (наприклад, ЕРС) легко отримати з загального визначення синусоїдної функції, а саме:
![]() .
.
Графічне зображення синусоїдної ЕРС наведене на рис. 4.2.
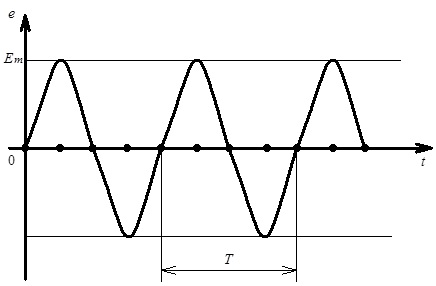
Рис. 4.2. Графічне зображення синусоїдної ЕРС
Найзручнішим виявилося зображення синусоїдної електричної величини деяким вектором, який обертається з постійною швидкістю ω та характеризується довжиною, що дорівнює амплітудному значенню цієї величини. При цьому миттєві значення відповідної величини відображаються проекціями цього вектора на вісь ординат (див. рис. 4.3, де у векторному вигляді відображена ЕРС).
Припустимо, що при t=0 (тобто в момент початку відліку часу) положення вектора відповідає співвідношенню:
![]() ,
,
де ψ1 - електричний кут, що визначає початкове значення ЕРС.
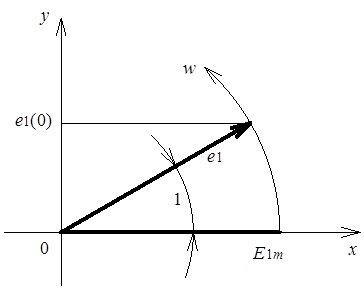
Рис. 4.3. Векторне відображення синусоїдної ЕРС (прийняті позначення: ![]() )
)
При подальшому обертанні вектора е1 його поточне положення визначатиметься співвідношенням:
![]() .
.
Кут ψ1, яким визначається початкове значення синусоїдної ЕРС (або іншої електричної величини – струму, напруги) зветься початковим фазним кутом або початковою фазою.
Припустимо, що в електричному колі діє ще одна ЕРС, початкове значення якої визначається як:
![]() ,
,
а поточне
![]()
Зазначимо, що частоти ЕРС Е1, Е2 однакові. Різниця початкових фаз цих двох ЕРС (в загальному випадку двох будь-яких синусоїдних електричних величин) зветься кутом зсуву фаз (часто, зсувом фаз) і визначається як:
![]() .
.
Куту зсуву фаз двох синусоїдних величин відповідає час:
![]() .
.
Час t12 показує на яку частку періоду (тобто на який відрізок часу) одна синусоїдна величина досягає своїх нульових (або амплітудних) значень раніше (пізніше) за другу. При цьому одна з двох електричних величин, що розглядаються, зветься випереджаючою за фазою, а друга – відстаючою. Про величини, для яких ψ12=0, говорять, що вони співпадають за фазою. Отже кут поточної фази синусоїдної величини з часом безперервно зростає, збільшуючись протягом періоду Т на величину 2p. Величина:
![]() .
.
показує швидкість, з якою змінюється кут поточної фази. Як вже було визначено ця величина зветься кутовою частотою на відміну від циклічної частоти f. Вимірюється кутова частота числом радіанів, на яке поточна фаза збільшується протягом секунди.
Наприклад, для частоти f=50 Гц кутова частота дорівнюватиме:
![]() .
.
Для співставлення синусоїдних величин їх зручно (зазвичай так і роблять) відображати у графічному або векторному вигляді на одному рисунку. Сукупність декількох синусоїд, що відображають синусоїдні величини, зветься хвильовою діаграмою. В загальному випадку частоти зображених на хвильовій діаграмі величин можуть бути різними. На рис. 4.4 наведена хвильова діаграма двох синусоїдних величин однакової частоти, але з різними початковими фазами, а саме:
![]() .
.
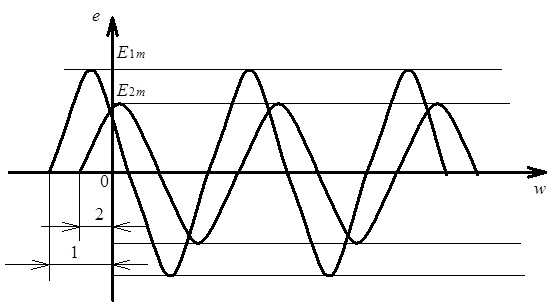
Рис. 4.4. Хвильова діаграма двох синусоїдних ЕРС однакової частоти й з
різними початковими фазами (![]() )
)
Сукупність декількох векторів, що відображають відповідні синусоїдні величини, зветься векторною діаграмою. При цьому частоти таких величин мають бути однаковими, щоб між векторами, які обертаються, зберігався постійний зсув фаз. На рис. 4.5 наведена векторна діаграма двох синусоїдних величин:
![]() .
.
Зазначимо, що довжини вказаних векторів е1, е2 відповідно дорівнюють Е1т, Е2т і, звичайно, залишаються незмінними в процесі обертання цих векторів навколо початку координат (з кутовою швидкістю w).
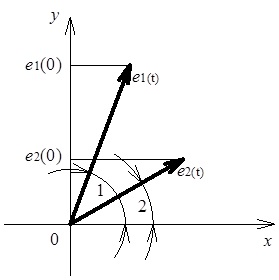
Рис. 4.5. Векторна діаграма двох синусоїдних ЕРС однакової частоти й з
різними початковими фазами (![]() )
)
Під час розрахунку електричних кіл синусоїдного струму доводиться додавати та віднімати значення синусоїдних струмів, напруги, ЕРС та ін. При цьому в кожен момент часу миттєві значення сумарної величини дорівнює алгебраїчній сумі миттєвих значень доданків.
Зважаючи на те, що миттєві значення синусоїдних величин відображаються проекціями векторів, які обертаються, вказані математичні операції над миттєвими значеннями електричних величин можна виконати як операції над відповідними векторами (див. рис. 4.6).
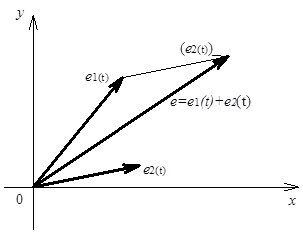
Рис. 4.6. Ілюстрація додавання миттєвих значень двох ЕРС
2. Елементи електричних кіл синусоїдного струму та їх властивості
Розглянуті в розділі 1 елементи електричних кіл в умовах дії синусоїдного струму проявляють характерні властивості, які пов’язані з фізичними явищами взаємодії змінного струму (змінного електромагнітного поля) з матеріальними об’єктами, виготовленими з різних матеріалів.
2.1. Резистивний елемент в електричному колі змінного струму
Як було встановлено в розділі 1 властивості резистивного елемента, що проявляються в електричному колі, обумовлені активним опором, який характеризує здатність такого елемента перетворювати електричну енергію на теплову. При цьому вольт-амперна характеристика такого елемента є прямою лінією. Отже, при проходженні електричного струму крізь резистивний елемент на виводах такого елемента реєструється напруга, яка відрізняється від струму виключно амплітудним значенням.
Припустимо, що до резистивного елемента приєднане деяке джерело живлення, а саме джерело синусоїдної напруги:
![]() .
.
За таких умов, крізь резистивний елемент протікатиме струм:
![]() .
.
При цьому:
![]() .
.
Тобто, прикладена до резистивного елемента напруга спричинятиме проходження крізь цей елемент струму. Причому вказані напруга і струм співпадатимуть за фазою й відрізнятимуться амплітудою, як це показано на рис. 4.10.
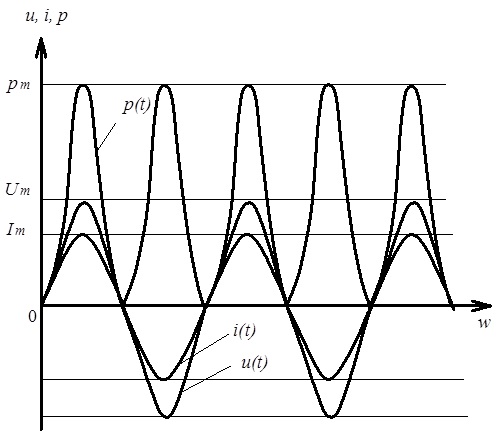
Рис. 4.10. Хвильова діаграма напруги, струму та потужності в резистивному елементі, включеному в електричне коло синусоїдного струму
Миттєва потужність, що розсіюватиметься резистивним елементом в електричному колі синусоїдного струму може бути розрахована як:
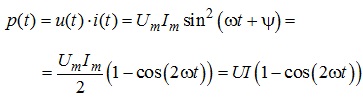
де U, I - діючі значення напруги на резистивному елементі та струму, що протікає крізь цей елемент.
Як видно, миттєва потужність має постійну складову UI та складову, що змінюється з подвійною, в порівнянні зі струмом (або напругою), частотою. Залежність p(t) наведена на рис. 4.10, де для спрощення прийнято
![]() .
.
Оскільки миттєві значення струму та напруги завжди мають однакові знаки, то і миттєва потужність, що розсіюється резистивним елементом завжди додатна. У межах періоду величина миттєвої потужності змінюється від нуля до
![]() .
.
Слід зупинитися на особливості, що притаманна елементам, виготовленим з провідникових матеріалів, при протіканні цими елементами змінного електричного струму. Активний опір таких елементів в електричному колі змінного струму відрізняється від активного опору тих самих елементів в колах постійного струму. Це обумовлене наявністю в провідникових матеріалах, якими протікає змінний струм, так званого поверхневого ефекту, завдяки якому один і той же елемент в колі змінного струму має більший опір, ніж в колі постійного струму, причому при підвищенні частоти струму активний опір елемента зростатиме. Поверхневий ефект проявляється в тому, що густина струму розподіляється нерівномірно в поперечному перерізі елемента, а саме: в центральній частині провідникового елемента густина виявляється суттєво меншою, ніж у поверхні. Такий розподіл густини струму аналогічний зменшенню площі поперечного перерізу елемента, а отже й збільшенню його опору.
2.2. Індуктивний елемент в електричному колі змінного струму
Індуктивний елемент – це елемент електричного кола з двома виводами, в якому відбувається запасання магнітної енергії (енергії магнітного поля), пов’язане з протіканням у колі електричного струму. При цьому вважається, що в такому елементі відсутні втрати електричної енергії та запасання електричної енергії (енергії електричного поля).
Кількісною мірою індуктивного елемента є індуктивність L. Нагадаємо, що термін «індуктивність» зазвичай використовують не тільки як характеристику, але як і назву самого індуктивного елемента.
Як вже нами було встановлено, при проходженні струму крізь індуктивний елемент (індуктивність) навколо останнього утворюється магнітне поле, яке графічно відображається магнітними силовими лініями, що огинають провідники зі струмом і завжди замкнені (див. рис. 4.11).
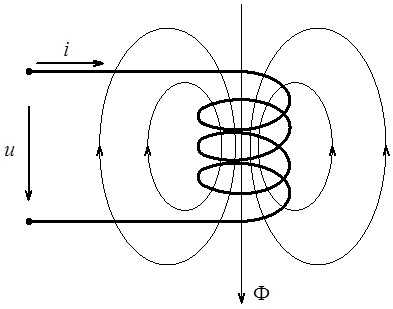
Рис. 4.11. Графічне відображення картини магнітного поля навколо індуктивного елемента
Нагадаємо, що магнітне поле характеризується напруженістю (Н) та індукцією (В), які є векторними величинами і відрізняються коефіцієнтом, що зветься магнітною проникністю. Зазвичай магнітна проникність позначається як m, а для вакууму - m0.
Магнітне поле утворює магнітний потік (Ф) – скалярну величину, що кількісно характеризує поширення магнітного поля крізь визначену поверхню.
Напруженість магнітного поля (як вже було зазначено в розділі 1) вимірюється в «амперах на метр» (А/м), індукція – у тесла (Тл), магнітний потік – у веберах (Вб).
З витками котушки індуктивності зціплені відповідні магнітні потоки, тобто з поверхнею, що утворюється контуром кожного витка котушки, пов’язана визначена напруженість (індукція) її магнітного поля. Ці магнітні потоки, звичайно, неоднакові для різних витків котушки, адже витки котушки в загальному випадку не можуть бути однаковими (число ліній магнітного поля, яке зціплене з окремими витками, неоднакове). Загальний магнітний потік, що зціплений з котушкою індуктивності (потокозчеплення) визначається як алгебраїчна сума магнітних потоків, зціплених з окремими витками цієї котушки, тобто:
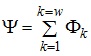 (4.8)
(4.8)
Зважаючи на те, що за умови відсутності феромагнітних тіл згідно закону повного струму напруженість магнітного поля пропорційна струму, матимемо:
![]() (4.9)
(4.9)
Відповідно до (4.9) величина індуктивності визначається як:
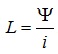 (4.10)
(4.10)
Як вже було відмічено, індуктивність вимірюється у генрі (Гн):
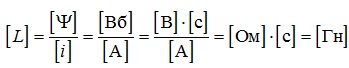 .
.
Зв'язок між струмом, що протікає індуктивним елементом, та напругою на його полюсах встановлюється на підставі закону електромагнітної індукції: при зміненні магнітного потоку, зціпленого з контуром, в останньому наводиться ЕРС, величина якої дорівнює швидкості змінення цього потоку у часі, та направлена так, щоб викликаний цією ЕРС струм перешкоджав зміненню потоку, який цей струм наводить.
Тобто, згідно закону
електромагнітної індукції, коли струм, протікаючи у додатному напрямку, зростає 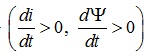 , ЕРС повинна мати полярність, яка при відсутності
зовнішнього джерела утворила б струм, спрямований назустріч струму i, який саме цю ЕРС і збуджує (завдяки якому ця ЕРС і
виникає). Такій полярності відповідає (за домовленістю) додатний напрямок
напруги на індуктивному елементі. Таким чином:
, ЕРС повинна мати полярність, яка при відсутності
зовнішнього джерела утворила б струм, спрямований назустріч струму i, який саме цю ЕРС і збуджує (завдяки якому ця ЕРС і
виникає). Такій полярності відповідає (за домовленістю) додатний напрямок
напруги на індуктивному елементі. Таким чином:
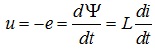 (4.11)
(4.11)
З (4.11) за величиною напруги на індуктивному елементі можна визначити струм, який крізь цей елемент протікає, а саме:
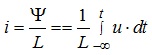 (4.12)
(4.12)
У співвідношенні (4.12) нижня межа інтегрування t = -∞ означає необхідність підсумовування всіх попередніх змінень напруги на індуктивному елементі до моменту часу t, тобто визначає необхідність врахування передісторії змінень величини u. При цьому зазвичай приймається:
u = 0 за умови, що t = -∞ (4.13)
З урахуванням (4.13) співвідношення (4.12) можна подати як:
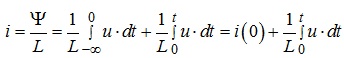 (4.14)
(4.14)
Тобто, відповідно до (4.14) величина струму, що протікає крізь індуктивний елемент у момент часу t визначається як сума двох доданків, один з яких характеризує значення струму у момент часу (t = 0), тобто у початковий момент часу, а другий – всі змінення значення струму від початкового до поточного моменту часу. Значення струму крізь елемент у початковий момент часу при розв’язанні задач зазвичай називають початковими умовами.
Зазначимо, що графічне
зображення залежності струму (напруги) від часу часто називають епюрами струму (напруги). Важливо відмітити, що
потокозчеплення та струм неперервні, тобто не можуть змінюватися стрибком, адже
лише в цьому випадку величина ![]() є величиною
кінцевою. Математично вказані умови
можна записати як:
є величиною
кінцевою. Математично вказані умови
можна записати як:
![]() .
.
Енергія, що може запасатися індуктивністю (накопичуватися в індуктивному елементі) визначається як:
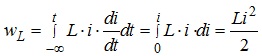 (4.15)
(4.15)
При виводі співвідношення (4.15) прийнято, що при t = -∞ величина струму, який протікає крізь індуктивний елемент, дорівнює нулю. Величина енергії, що накопичується в індуктивності, звичайно, не може мати від’ємного значення, що й підтверджується співвідношенням (4.15).
Припустимо, що включеною до електричного кола індуктивністю протікає синусоїдний струм, миттєве значення якого визначається як:
![]() .
.
При цьому на виводах індуктивності виникає ЕРС:
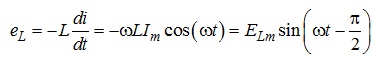 ,
,
де ![]() - амплітудне
значення цієї ЕРС.
- амплітудне
значення цієї ЕРС.
Зважаючи на те, що:
![]() ,
,
співвідношення для миттєвого значення напруги на виводах індуктивності матиме вигляд:
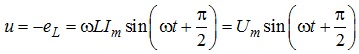 ,
,
де![]() .
.
Зрозуміло, що для діючих значень напруги та струму, відповідно, матимемо співвідношення:
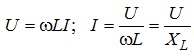 ,
,
де ![]() - індуктивний опір.
- індуктивний опір.
Миттєва потужність електричного струму, що пов’язана з індуктивністю, характеризує швидкість перетворення електричної енергії джерела живлення в енергію магнітного поля.
Вказана миттєва потужність визначається як:
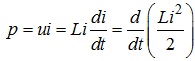 .
.
З останнього співвідношення видно, що за умови співпадіння знаків u та i (в процесі змінення цих величин) величина потужності додатна, що відповідає запасанню енергії індуктивним елементом, тоді як за умови не співпадіння знаків u та i потужність матиме від’ємне значення (від’ємна потужність), що відповідає віддаванню (попередньо накопиченої) енергії індуктивним елементом у зовнішнє (по відношенню до цієї індуктивності) електричне коло.
За умови, що напруга та струм змінюються за синусоїдним законом, матимемо:
![]() .
.
На рис. 4.13 показані часові залежності струму, напруги, миттєвої потужності та ЕРС, пов’язані з індуктивним елементом.
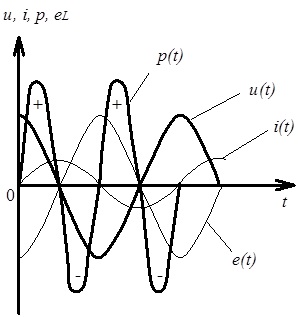
Рис. 4.13. Часові залежності струму, напруги, потужності та ЕРС в електричному колі синусоїдного струму з індуктивністю
З рис. 4.13 видно, що в електричному колі з індуктивністю відбувається виключно періодичний обмін енергією між генератором і магнітним полем відповідно до зростання та спадання енергії магнітного поля, яка визначається як:
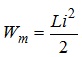 .
.
При вказаному обміні енергії не відбуваються її перетворення в механічну або теплову енергію.
Отже середня за період активна потужність в електричному колі з індуктивністю дорівнює нулю. За міру швидкості обміну енергії в електричному колі приймають максимальне значення миттєвої потужності, яка зветься реактивною потужністю і визначається як
![]() .
.
Ще раз підкреслимо, що реактивна потужність (як в індуктивності, так і в інших елементах електричного кола змінного струму) не пов’язане з перетворенням електричної енергії в енергію інших видів, а отже і не пов’язана з виконанням якоїсь корисної роботи.
Реактивна потужність характеризує виключно процеси обміну електричної енергії між окремими елементами відповідного електричного кола. На рис. 4.14 наведена векторна діаграма, яка характеризує зсув фаз між струмом, що протікає індуктивністю, та напругою й ЕРС на виводах цього елемента.
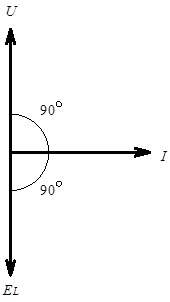
Рис. 4.14. Векторна діаграма, яка характеризує зсув фаз між струмом, що протікає індуктивністю, та напругою і ЕРС на її виводах
З рис. 4.14 видно, що синусоїдний струм, який протікає індуктивністю, напругою й ЕРС на виводах цієї індуктивності взаємно ортогональні.
2.3. Ємнісний елемент в електричному колі змінного струму
Як вже було визначено раніше, ємнісний елемент – це елемент електричного кола з двома виводами, в якому відбувається запасання електричної енергії (енергії електричного поля), пов’язане з протіканням у колі електричного струму. При цьому вважається, що в такому елементі відсутні втрати електричної енергії та запасання магнітної енергії (енергії магнітного поля).
Кількісною мірою ємнісного елемента є ємність С.
Прикладом ємнісного елемента, як вже було зазначено в розділі 1, може слугувати високоякісний конденсатор постійної ємності. В даному випадку категорія якості характеризуватиме відсутність індуктивності виводів та пластин (обкладинок) конденсатора. а також втрат енергії у виводах, пластинах та діелектрику, яким зазвичай заповнюється (для збільшення ємності конденсатора) прошарок між вказаними пластинами.
Відомо, що заряд q, який накопичується на пластинах конденсатора, та напруга на його виводах, пов’язані співвідношенням:
![]() (4.16)
(4.16)
де С - електрична ємність, яка вимірюється у фарадах (Ф).
Диференціювання (4.16) за часом приводить до співвідношення:
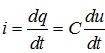 (4.17)
(4.17)
Співвідношення (4.17) свідчить про те, що струм, який протікає крізь ємнісний елемент, визначається швидкістю змінення напруги на виводах цього елемента. При постійній напрузі на виводах ємнісного елемента струм крізь нього не протікає (дорівнює нулю), що відповідає розриву електричного кола.
Зазначимо, що струм, який протікає крізь ємнісний елемент, часто називають зарядним струмом, тобто струмом, що заряджає цей елемент (переносить електричний заряд на його пластини). На підставі (4.16), (4.17) неважко встановити, що:
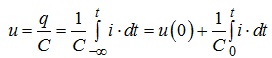 (4.18)
(4.18)
Заряд та напруга на
ємнісному елементі не можуть змінюватися стрибком, адже лише в цьому випадку
похідна ![]() матиме кінцеве
значення. Математично вказане положення
подається як:
матиме кінцеве
значення. Математично вказане положення
подається як:
![]() .
.
Енергія, що може запасатися ємнісним елементом (накопичуватися у ємності) визначається як:
![]() (4.19)
(4.19)
При виводі співвідношення (4.19) прийнято, що при t = - ∞ величина напруги на виводах ємності дорівнює нулю.
Величина енергії, що накопичується у ємнісному елементі, звичайно, не може мати від’ємного значення.
Припустимо, що до виводів включеної до електричного кола ємності прикладена напруга, миттєве значення якої визначається як:
![]() .
.
При цьому відбувається перезарядження ємності струмом:
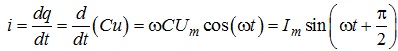 ,
,
де ![]() - амплітудне
значення струму перезаряду.
- амплітудне
значення струму перезаряду.
Переходячи від амплітудних значень струму та напруги до діючих значень, отримуємо співвідношення:
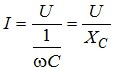
де ![]() - ємнісний опір.
- ємнісний опір.
Миттєва потужність, що розсіюється ємнісним елементом у колі змінного струму, характеризує швидкість перетворення енергії джерела живлення в енергію електричного поля, яка накопичується ємністю. Вказана миттєва потужність визначається як:
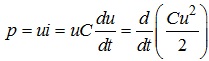 (4.20)
(4.20)
З (4.20) видно, що (як і при розгляді індуктивності) за умови співпадіння знаків при u та i величина потужності додатна, що відповідає запасанню енергії ємнісним елементом, а за умови не співпадіння знаків u та i величина потужності від’ємна (від’ємна потужність), що відповідає віддаванню енергії ємнісним елементом у зовнішнє (по відношенню до даного ємнісного елемента) електричне коло.
Підставляючи в отримане співвідношення миттєвої потужності (4.20), миттєві значення струму та напруги, що змінюються за синусоїдним законом, а саме значення
![]()
отримуємо:
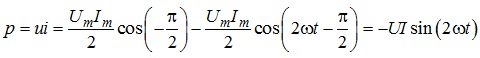 .
.
На рис. 4.16 наведені часові залежності миттєвих значень напруги, струму та потужності, притаманних електричному колу з ємнісним елементом.
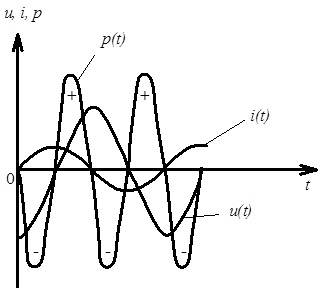
Рис. 4.16. Часові залежності миттєвих значень напруги, струму та потужності в електричному колі з ємнісним елементом
На рис. 4.17 наведена векторна діаграма, якою відображається зсув фаз між струмом і напругою в електричному колі з ємністю.
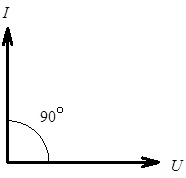
Рис. 4.17. Векторна діаграма струму й напруги в електричному колі з ємнісним елементом
Таким чином в електричному колі з ємнісним елементом відбувається періодичний обмін енергією між генератором і електричним полем ємності.
Швидкість вказаного обміну характеризує максимальне значення потужності обміну – реактивну потужність, яка визначається формулою:
![]() .
.
2.4. Дуальність елементів електричного кола
Між співвідношеннями, якими визначаються характеристики резистивного, індуктивного та ємнісного елементів існує визначений зв'язок. Для виявлення цього зв’язку запишемо ці співвідношення у вигляді, поданому табл. 4.1.
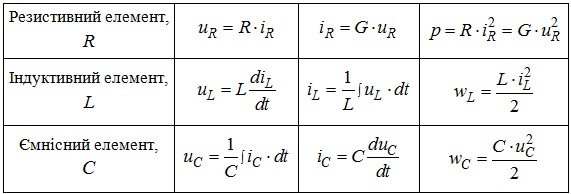
З табл. 4.1 видно, що між співвідношеннями, якими визначаються напруга на виводах елементів, струм, що протікає крізь елементи та енергія, що розсіюється тим чи іншим елементом, існує аналогія при заміні струмів напругою і навпаки. Такі співвідношення звуться дуальними, а елементи, характеристики яких дуальні – звуться дуальними елементами.
Поняття дуальності є взаємним.
Характеристики та елементи електричного кола, які можуть бути дуально та взаємно замінені можна відобразити, як:
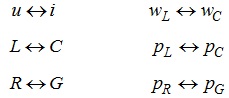
3. Послідовне з’єднання елементів в електричному колі синусоїдного струму
Фрагмент (ізольовану вітку) електричного кола з послідовним з’єднанням опору, індуктивності та ємності наведено на рис. 4.18.
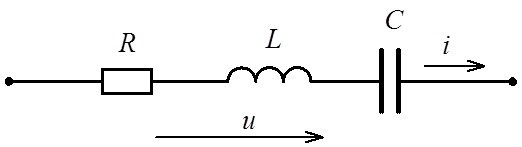
Рис. 4.18. Вітка електричного кола з послідовним з’єднанням резистивного, індуктивного та ємнісного елементів
Таке з’єднання часто зустрічається в структурі електричних кіл змінного струму. Воно може формуватися як «навмисно» з відповідних елементів електричного кола, так і «не санкціоновано», тобто утворюватися за рахунок наявності визначених «паразитних» складових у реальних елементах. Специфічні властивості такого з’єднання в електричному колі синусоїдного струму потребують детального вивчення.
3.1. Загальні характеристики послідовного з’єднання R, L, C елементів
Припустимо, що миттєве значення струму у наведеній на рис. 4.18 вітці електричного кола визначається як:
![]() .
.
При цьому миттєві, амплітудні та ефективні значення напруги на окремих елементах кола дорівнюватимуть:
на активному опорі
![]() ;
;
на індуктивності
![]()
на ємності
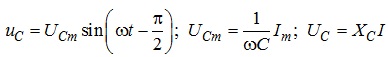 .
.
Визначаємо напругу на всій ділянці кола
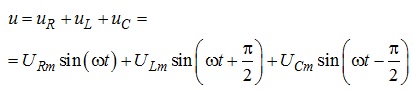
Напруга на ділянці електричного кола з послідовним з’єднанням активного опору, індуктивності та ємності містить дві складові:
- активну ua,
- реактивну up.
Вказані складові напруги на ділянці електричного кола з послідовним з’єднанням R, L, C елементів пов’язані з напругою на окремих елементах як:
![]() .
.
Розглянемо реактивну складову напруги детальніше, з урахуванням миттєвих значень напруги на індуктивності та ємності. При цьому матимемо:
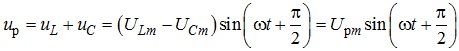 .
.
З останнього співвідношення видно, що характер реактивної складової напруги визначається взаємною величиною амплітудних значень напруги на ємності та індуктивності. При цьому можна виділити три типи цих взаємних значень, а саме:
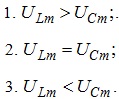
Звичайно, що характер співвідношень ефективних значень напруги UL та UC буде співпадати з наведеним характером співвідношень амплітудних значень відповідних напруг. Розглянемо перший з вказаних типів взаємних значень напруги на індуктивності та ємності, а саме:
![]() .
.
З цією метою побудуємо
відповідну векторну діаграму (див. рис. 4.19, де представлені співвідношення для ефективних
значень).
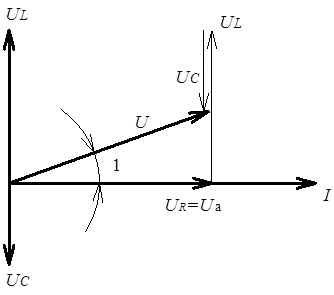
Рис. 4.19.
Векторна діаграма для напруги на елементах електричного кола з послідовним
з’єднанням R, L, C елементів
за умови ![]()
При побудові наведеної векторної діаграми враховано, що:
- зсув фаз між струмом в колі та напругою на резисторі відсутній, тобто вектори струму та напруги uR співпадають за напрямком (колінеарні);
- зсув фаз між напругою
на резисторі та напругою на індуктивності додатний і дорівнює
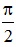 ;
; - зсув фаз між напругою
на резисторі та напругою на ємності відємний і дорівнює
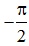 .
.
З побудованої векторної діаграми встановлюємо, що:
![]() ,
,
де прийнято
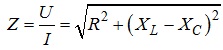
Величина Z зветься повним опором відповідної ділянки електричного кола, або якогось елемента (в даному випадку ділянки кола, що містить резистор, індуктивність та ємність). При цьому фазовий кут φ сумарної напруги U на кінцях з’єднання резистора, індуктивності та ємності, як видно з векторної діаграми, поданої на рис. 4.19, можна визначити зі співвідношень:
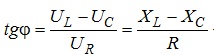
або
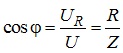 .
.
Умовно приймемо (і надалі будемо дотримуватися цього прийнятого положення), що:
- за умови
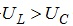 (струм відстає за
фазою від напруги) кут зсуву фаз додатний,
(струм відстає за
фазою від напруги) кут зсуву фаз додатний, - за умови
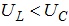 (струм випереджає
напругу) зсув фаз від’ємний.
(струм випереджає
напругу) зсув фаз від’ємний.
Ці умови відповідатимуть обертанню векторів, показаному на рис. 4.19, тобто проти годинникової стрілки.
Наведеному вище положенню відповідатиме цілком конкретний запис початкових фаз напруги та струму. Так, за умови прийняття як первісну категорію напругу у вигляді:
![]()
струм записуватиметься як:
![]() .
.
При цьому позначення кута φ включає й відповідний знак цього кута.
Зазначимо, що від побудованої векторної діаграми зміною масштабу легко перейти до трикутника опорів (наприклад, зменшивши всі сторони відповідних векторів в I разів), як показано на рис. 4.20.
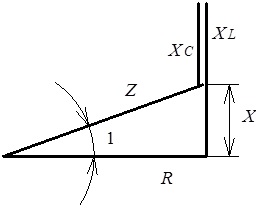
Рис. 4.20.
Трикутник опорів вітки електричного кола з послідовним з’єднанням R, L, C елементів за умови ![]()
З рис. 4.20 видно, що в трикутнику опорів повний опір Z є гіпотенузою, R - катетом, який прилягає до кута φ, а величина сумарного реактивного опору, яка в даному випадку визначається співвідношенням
![]()
є катетом, який протилежний до кута φ.
Векторні діаграми та трикутники опорів для співвідношення:
![]()
наведені на рис. 4.21 та рис. 4.22, відповідно.
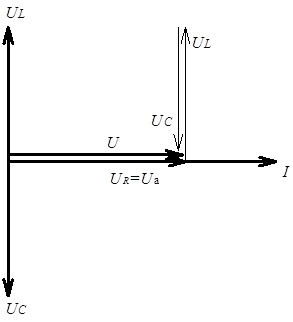
Рис. 4.21.
Векторна діаграма для напруги на елементах вітки електричного кола з
послідовним з’єднанням R, L, C елементів
за умови ![]()
З рис. 4.21 видно, що в даному випадку зсув фаз між струмом і напругою дорівнюватиме нулю:
![]() .
.
Отже, у вітці електричного кола з послідовним з’єднанням R, L, C елементів за умови:
![]()
початкові фази струму й напруги – однакові (струм і напруга – синфазні).
З рис. 4.22 видно, що за умови:
![]()
трикутник опорів вироджується у пряму лінію, яка співпадає з активним опором. Такий режим електричного кола зветься резонансним.
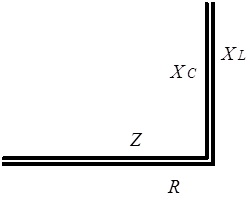
Рис. 4.22.
Трикутник опорів вітки електричного кола з послідовним з’єднанням R, L, C елементів за умови ![]()
Резонансний режим послідовного з’єднання індуктивності та ємності характеризується рівністю напруги на цих елементах та зветься резонансом напруги або послідовним резонансом. Легко бачити, що в режимі резонансу напруги струм у колі буде максимальним і визначатиметься виключно опором резистора та, звичайно, величиною прикладеною до даної ділянки кола напруги. Резонансне явище у вітці електричного кола з послідовним з’єднанням R, L, C елементів детально розглядатиметься в подальшому. Векторні діаграми та трикутники опорів вітки електричного кола з послідовним з’єднанням R, L, C елементів для співвідношення:
![]()
наведені на рис. 4.23 та рис. 4.24, відповідно.
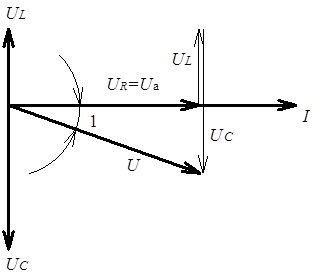
Рис. 4.23. Векторна діаграма для напруги на елементах вітки електричного
кола з послідовним з’єднанням R, L, C елементів
за умови ![]()
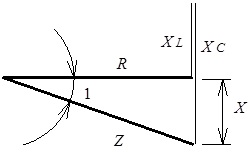
Рис. 4.24. Трикутник опорів вітки електричного кола з послідовним з’єднанням
R, L, C елементів за умови ![]()
З рис. 4.23 видно що, за
умови ![]() струм у вітці
електричного кола з послідовним з’єднанням R, L, C елементів
випереджає напругу на кут φ (нагадаємо, що при визначенні
співвідношення фаз струму й напруги на векторній діаграмі нами прийняте
обертання векторів проти годинникової стрілки).
струм у вітці
електричного кола з послідовним з’єднанням R, L, C елементів
випереджає напругу на кут φ (нагадаємо, що при визначенні
співвідношення фаз струму й напруги на векторній діаграмі нами прийняте
обертання векторів проти годинникової стрілки).
З трикутнику опорів,
поданому на рис. 4.24, видно, що сумарний реактивний опір електричного кола з
послідовним з’єднанням R, L, C елементів
за умови ![]() матиме від’ємне
значення. Миттєва потужність в
електричному колі, утвореному послідовним з’єднанням резистора, індуктивності
та ємності визначається як:
матиме від’ємне
значення. Миттєва потужність в
електричному колі, утвореному послідовним з’єднанням резистора, індуктивності
та ємності визначається як:
![]() .
.
Припустимо, що струм визначається співвідношенням:
![]() .
.
За таких умов миттєва потужність може бути подана як:
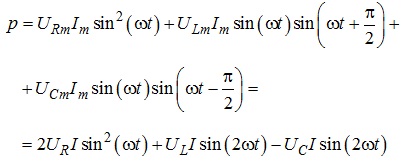
З наведеного співвідношення видно, що в електричному колі з послідовним з’єднанням резистора індуктивності та ємності відбувається перетворення електричної енергії на теплову енергію (що відповідає першому доданку), а також обмін енергії між генератором та магнітним (другий доданок) і електричним (третій доданок) полями.
Відповідно до процесів, які відбуваються в електричному колі з послідовним з’єднанням резистора, індуктивності та ємності, можна виділити три види потужності, а саме:
- середню за період або активну потужність, яка пов’язана з наявністю резистора та визначається як
![]() ;
;
- реактивну потужність, яка пов’язана з наявністю індуктивності та ємності й визначається як
![]() ;
;
- повну потужність, яка пов’язана з наявністю всіх трьох елементів та визначається як
![]() .
.
Зазначимо, що активна,
реактивна та повна потужності пов’язані між собою як сторони прямокутного
трикутника (так званого, трикутника
потужностей), який легко побудувати, наприклад, на підставі векторної
діаграми. На рис. 4.25 як приклад
наведений трикутник потужностей для вітки електричного кола, що розглядається,
у випадку ![]() .
.
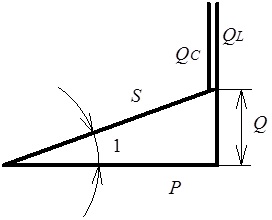
Рис. 4.25. Трикутник потужностей для вітки електричного кола з послідовним з’єднанням R, L, C елементів за умови ![]()
Як видно з рис. 4.25, між активною, реактивною та повною потужностями існують співвідношення:
![]() .
.
На рис. 4.26
ілюструється характер змінення у часі миттєвих значень як повної потужності (р),
так і її окремих складових ![]() , відповідно до змінення миттєвого значення струму, що
протікає в електричному колі з послідовним з’єднанням R, L, C за умови
, відповідно до змінення миттєвого значення струму, що
протікає в електричному колі з послідовним з’єднанням R, L, C за умови ![]() .
.
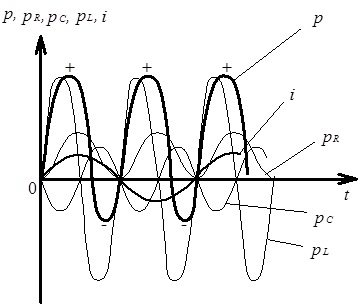
Рис. 4.26. Миттєві значення повної потужності (р) та її окремих складових
![]() , по відношенню
, по відношенню
до миттєвого значення струму і, який
протікає у вітці електричного кола з послідовним з’єднанням R, L, C елементів
за умови ![]()
Як видно повна потужність на окремих відрізках часу має від’ємне значення. Це обумовлено наявністю в електричному колі реактивних елементів та означає, що в ці періоди часу потужність повертається до джерела живлення.
3.2. Резонанс напруги
Резонанс напруги спостерігається у вітці електричного кола, де послідовно з’єднанні індуктивність та ємність. Послідовно з вказаними елементами, звичайно, може бути включений і резистивний елемент (див. рис. 4.27), який визначає втрати на відповідній ділянці електричного кола.
Резонанс напруги часто називають послідовним резонансом, відповідно до виду з’єднання (виду ділянки електричного кола), в якому такий резонанс проявляється.
Умовою резонансу напруги у вітці електричного кола з послідовним з’єднанням R, L, C елементів в термінах напруги є однаковість напруги на індуктивному й ємнісному елементах, тобто умова
![]() .
.
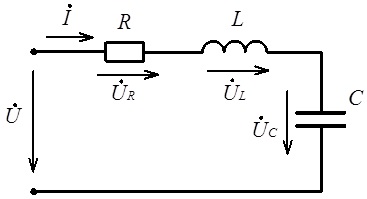
Рис. 4.27. Електричне коло до ілюстрації резонансу напруг
Неважко переконатися, що вказану умову резонансу напруги в термінах реактивного опору елементів можна подати як:
![]() (4.21)
(4.21)
Підставляючи у (4.21) вирази реактивних опорів індуктивності та ємності, отримуємо:
![]() (4.22)
(4.22)
Розв’язок рівняння (4.22), дозволяє встановити значення частоти:
![]() ,
,
при якій саме й відбувається явище резонансу, а саме:
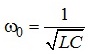 (4.23)
(4.23)
Частота w0 зветься резонансною частотою.
Повний опір послідовного з’єднання резистора, індуктивності та ємності на резонансній частоті матиме активний характер і дорівнюватиме опору резистора, тобто:
![]() (4.24)
(4.24)
Для електричного кола, де спостерігається резонанс напруги, вводять поняття характеристичного опору.
Характеристичний опір вітки електричного кола з послідовним з’єднанням R, L, C елементів – це величина, яка дорівнює реактивному опору індуктивності або ємності на резонансній частоті.
Характеристичний опір, за своєю суттю, характеризує співвідношення між індуктивністю та ємністю відповідного електричного кола. Дійсно, в точці резонансу матимемо:
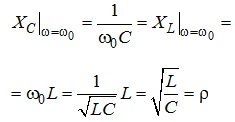 (4.25)
(4.25)
Струм в електричному колі на частоті резонансу сягає максимального значення, яке дорівнює:
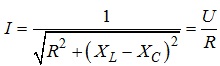 (4.26)
(4.26)
Напруги на індуктивності та ємності на частоті резонансу однакові за амплітудою, але зсунуті за фазою на p рад. Діюче (а отже й амплітудне) значення напруги на реактивних елементах на частоті резонансу дорівнюватиме:
![]() (4.27)
(4.27)
З (4.27) видно, що при r > R напруга на кожному з реактивних елементів в точці резонансу може суттєво перевищувати напругу джерела живлення, за рахунок відповідного перетворення енергії цього джерела на енергію, що накопичується реактивними елементами та «перетікає» між індуктивністю та ємністю.
Здатність електричного кола, що розглядається, накопичувати енергію характеризується категорією добротності, яку можна визначити як:
![]() (4.28)
(4.28)
Величина зворотна до добротності зветься затуханням кола:
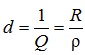 (4.29)
(4.29)
Для випадку резонансу напруги у вітці електричного кола, що розглядається, на рис. 4.28 наведено векторну, а на рис. 4.29 часову діаграми напруг та струму.
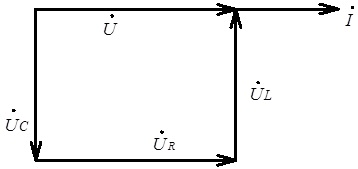
Рис. 4.28. Векторна діаграма розподілення напруги та струму у вітці електричного кола з послідовним з’єднанням R, L, C елементів на частоті резонансу
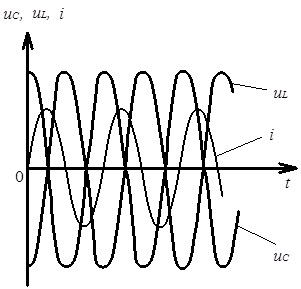
Рис. 4.29. Часові діаграми напруг та струму у вітці електричного кола з послідовним з’єднанням R, L, C елементів на частоті резонансу
На рис. 4.30 наведена часова діаграма потужностей, що пов’язані з елементами вітки електричного кола з послідовним з’єднанням R, L, C елементів.
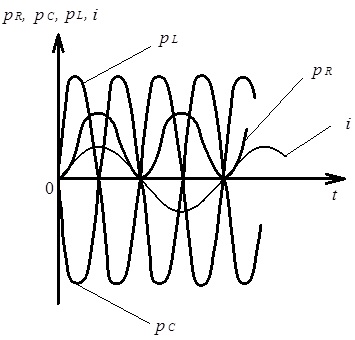
Рис. 4.30. Часова діаграма потужностей, що пов’язані з послідовним з’єднанням R, L, C елементів електричного кола на частоті резонансу
З рис. 4.30 видно, що в режимі резонансу напруги на індуктивності та ємності однакові за амплітудою й зсунуті за фазою на p рад. Саме це й приводить до їх взаємного нівелювання.
У вітці електричного кола з послідовним з’єднанням R, L, C елементів досягти умови резонансу можна за рахунок змінення частоти, індуктивності або ємності.
Залежності XL, XC від частоти називають частотними характеристиками електричного кола. На рис. 4.31 наведені частотні характеристики вітки електричного кола з послідовним з’єднанням R, L, C елементів.
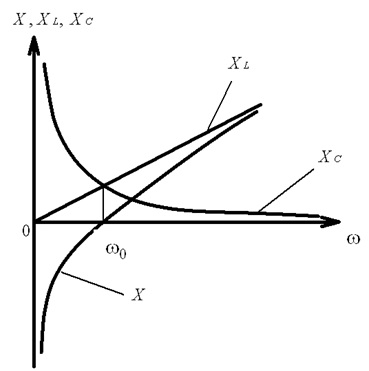
Рис. 4.31. Частотні залежності реактивних опорів вітки електричного кола з послідовним з’єднанням R, L, C елементів
Видно, що на частоті резонансу опори індуктивності та ємності урівнюються, а загальний реактивний опір Х відповідної вітки електричного кола дорівнюватиме нулю. Частотні залежності струму І та напруги UL, UC в електричному колі, де можливе явище резонансу, називають резонансними характеристиками цього кола. На рис. 4.32 наведена частотна залежність струму у вітці електричного кола з послідовним з’єднанням R, L, C елементів в області резонансу (резонансна характеристика струму). Для зручності резонансні характеристики електричних кіл, де можливе явище резонансу, часто будують відносно нормованої частоти, яку визначають як:
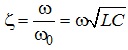 (4.30)
(4.30)
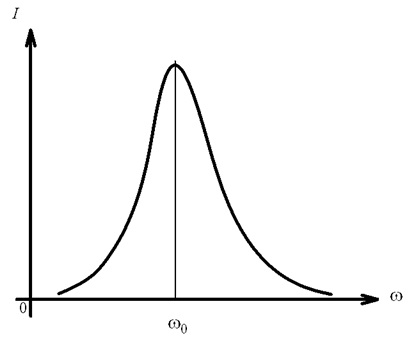
Рис. 4.32. Резонансна характеристика струму в області послідовного резонансу
Для отримання резонансної характеристики струму в електричному колі в залежності від введеної нормованої частоти здійснимо деякі алгебраїчні перетворення:
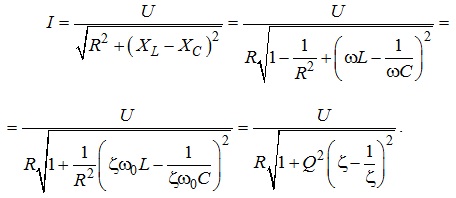
Величину
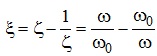
зазвичай називають узагальненою частотою.
Зважаючи на те, що при резонансі струм в електричному колі сягає максимального значення й дорівнює:
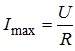 ,
,
резонансну характеристику кола доречно нормувати по відношенню до цього значення. Отже остаточно матимемо:
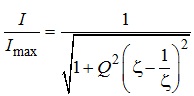 (4.31)
(4.31)
Зі співвідношення (4.31) видно, що резонансна характеристика електричного кола, побудована в нормованих координатах, визначається добротністю цього кола. На рис. 4.33, як приклад, наведені резонансні характеристики при різній добротності електричного кола.
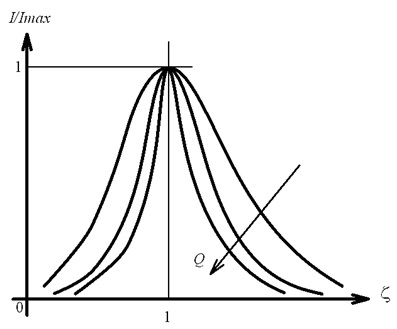
Рис. 4.33. Резонансні характеристики струму в області послідовного резонансу при різних значеннях добротності (стрілка Q вказує напрямок збільшення величини добротності)
З рис. 4.33 видно, що збільшення добротності веде до звужування резонансної характеристики. Для характеристики ступеня «вузькості» резонансних характеристик використовується поняття полоси пропускання.
Полоса
пропускання – це ширина резонансної характеристики на рівні, де струм менше за
максимальне значення в √2 разів. Тобто, для визначення
полоси пропускання ![]() необхідно знайти
точки перетину резонансної характеристики:
необхідно знайти
точки перетину резонансної характеристики:
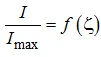
з лінією
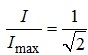 .
.
Виконавши відповідні перетворення, отримуємо:
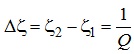 .
.
Отже полоса пропускання резонансної характеристики є величиною зворотною до добротності електричного кола, що наочно видно з рис. 4.33.
4. Електричні кола синусоїдного струму з паралельним з’єднанням елементів
Базові основи розрахунку електричних кіл змінного струму з паралельним з’єднанням окремих віток, до кожної з якої входять ті чи інші елементи, розглянемо на прикладі фрагменту електричного кола, зображеного на рис. 4.34.
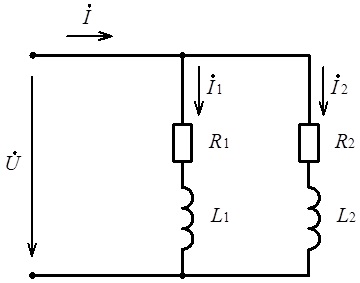
Рис. 4.34. Фрагмент електричного кола змінного струму з паралельним з’єднанням двох віток
4.1. Загальні характеристики електричного кола з паралельним з’єднанням окремих віток
Вважатимемо, що на вході електричного кола, представленого на рис. 4.34, діє синусоїдна напруга
![]() .
.
При цьому у вітках електричного кола протікатимуть струми
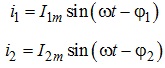
Амплітудні значення струмів І1т, І2т в кожній вітці, відповідні величини зсуву фаз φ1, φ2 та повні опори Z1,Z2 цих віток визначаються аналогічно наведеному вище, а саме:
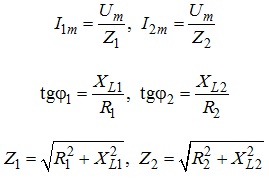
Під час розрахунку електричних кіл з паралельним з’єднанням окремих елементів (віток) доцільно користуватися категоріями провідності Y цих елементів (віток). Нагадаємо, що величина провідності елемента електричного кола зворотна до величини його опору. Це положення справедливе для опорів як активних, так і для реактивних та повних. Отже для електричного кола, що розглядається, матимемо:
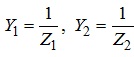 .
.
Амплітудні значення струмів у вітках електричного кола у термінах провідності запишуться як:
![]()
В нерозгалуженій частині електричного кола струм відповідно до першого закону Кірхгофа дорівнюватиме
![]() .
.
Побудуємо векторну діаграму для напруги та визначених значень струмів у вітках електричного кола (див. рис. 4.35).
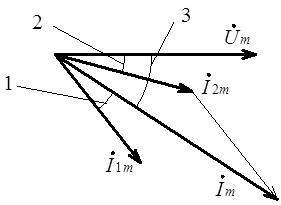
Рис. 4.35. Векторна діаграма напруги та струмів в електричному колі з
паралельним з’єднанням двох віток ![]()
З наведеної векторної
діаграми видно, що струм Im у нерозгалуженій частині електричного кола, є сумою (векторною)
струмів I1m, I2m. Величину цього струму можна розрахувати, використовуючи
відому теорему косинусів для трикутника, утвореного векторами ![]() .
.
Таким чином, для амплітудного значення струму у нерозгалуженій частині електричного кола матимемо:
![]() .
.
Кут зсуву фази струму у нерозгалуженій частині кола, що розглядається, також легко встановити з наведеної на рис. 4.35 векторної діаграми, а саме:
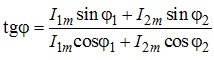 .
.
Наведений алгоритм розрахунку струмів в електричному колі з паралельним з’єднанням віток (елементів) стає надто громіздким при збільшенні кількості віток. Спрощення алгоритму можна отримати за умови введення (за аналогією з аналізом послідовного з’єднання елементів) категорій активної та реактивної складової струмів (а отже й активних та реактивних провідностей). З цією метою розкладемо струми, що протікають в електричному колі на дві ортогональні складові, а саме: на активну складову Іа, спрямовану вздовж осі абсцис, та реактивну складову Ір, спрямовану вздовж осі ординат. За таких умов кожен зі струмів електричного кола дорівнюватиме векторній сумі відповідних складових, одна з яких відображає активну складову струму, а друга – реактивну. Відповідна векторна діаграма подана на рис. 4.36.
Згідно наведеної векторної діаграми для вітки 1:
- активна складова струму
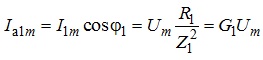 ;
;
- реактивна складова струму
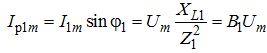 ;
;
де
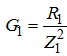 - активна
провідність вітки 1;
- активна
провідність вітки 1;
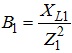 - реактивна
провідність вітки 1.
- реактивна
провідність вітки 1.
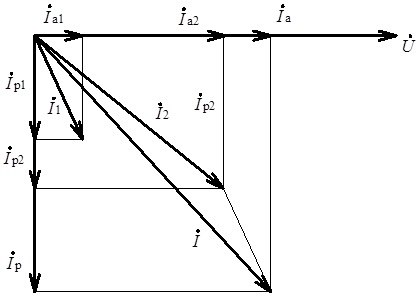
Рис. 4.36. Векторна діаграма представлених активною та реактивною складовими струмів електричного кола з паралельним з’єднанням віток
Знову ж таки на підставі наведеної діаграми для вітки 2:
- активна складова струму
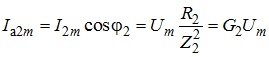 ;
;
- реактивна складова струму
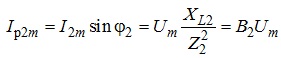 ,
,
де
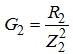 - активна
провідність вітки 2;
- активна
провідність вітки 2;
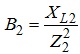 - реактивна
провідність вітки 2.
- реактивна
провідність вітки 2.
За таких умов відповідно до наведеної векторної діаграми струми першої та другої вітки електричного кола відповідно визначаються як:
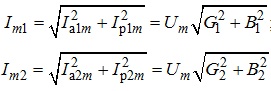 ,
,
де
![]() - повна провідність
першої вітки;
- повна провідність
першої вітки;
![]() - повна провідність
другої вітки.
- повна провідність
другої вітки.
З наведених формул, якими визначають повні провідності віток електричного кола, видно, що активна, реактивна та повна провідності пов’язані між собою як сторони прямокутного трикутника. Такий трикутник зветься трикутником провідностей (див. рис. 4.37). На підставі наведених співвідношень амплітудне значення струму в електричному колі до точки розгалуження (до відповідного вузла) та активну й реактивну складові цього струму можна подати як:
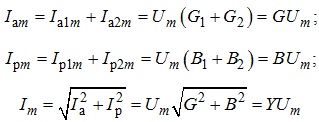
де
![]() - активна складова
загальної провідності обох віток;
- активна складова
загальної провідності обох віток;
![]() - реактивна складова
загальної провідності обох віток;
- реактивна складова
загальної провідності обох віток;
![]() - повна провідність
обох віток електричного кола;
- повна провідність
обох віток електричного кола;
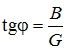 - тангенс кута між
повною провідністю та її активної складової.
- тангенс кута між
повною провідністю та її активної складової.
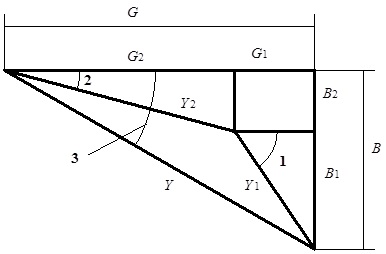
Рис. 4.37. Трикутник провідностей для електричного кола з двома
паралельними вітками ![]()
Активна, реактивна та повна потужність в електричному колі, що розглядається, визначаються як:
- активна потужність
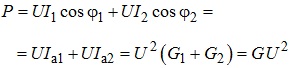
- реактивна потужність
![]() ;
;
- повна потужність
![]() .
.
За умови наявності у колі паралельних віток, одна (або більше) з яких містить ємнісний елемент, задача розв’язуватиметься аналогічно з урахуванням того, що реактивна складова ємнісної провідності від’ємна. При цьому може статися ситуація, за якої реактивні складові віток з індуктивностями дорівнюватимуть реактивним складовим віток з ємностями, а отже реактивна складова з’єднання таких віток дорівнюватиме нулю. Такий режим електричного кола зветься резонансом струмів і характеризується мінімальною провідністю з’єднання віток, а отже й мінімальним струмом у нерозгалуженій частині кола.
4.2. Резонанс струмів
Явище резонансу струмів проявляється в електричних колах, де індуктивність та ємність включені паралельно. Такий резонанс іноді називають паралельним резонансом.
Для виявлення основних властивостей цього явища розглянемо електричне коло зображене на рис. 4.38, де паралельно до індуктивності та ємності підключений резистор, опір якого відображає дисипативні (теплові) втрати в елементах кола.
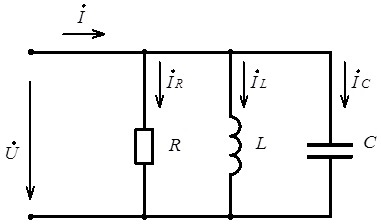
Рис. 4.38. Схема електричного кола до ілюстрації резонансу струмів
Умовою резонансу струму є:
![]() (4.32)
(4.32)
Тобто резонанс струмів відбуваються в електричних колах з паралельним з’єднанням індуктивності та ємності за умови, що провідність цих елементів однакова.
З умови резонансу неважко знайти значення резонансної частоти (аналогічно тому, як це було зроблено при аналізі явища послідовного резонансу), а саме:
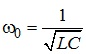 (4.33)
(4.33)
На рис. 4.39 наведені частотні залежності реактивних провідностей електричного кола в області паралельного резонансу (резонансу струмів).
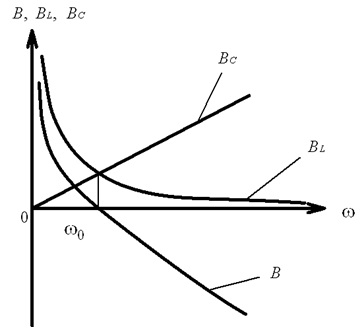
Рис. 4.39. Частотна залежність реактивних провідностей електричного кола в області паралельного резонансу
За умови резонансу струм І у нерозгалуженій частині електричного кола, що розглядається, становитиме:
![]() (4.34)
(4.34)
З (4.34) видно, що за умови резонансу струмів (тобто на частоті резонансу) струм у нерозгалуженій частині електричного кола сягає мінімальної величини, а його фазовий кут співпадає з фазовим кутом прикладеної до електричного кола напруги. Це наочно відображається на відповідній векторній діаграмі (див. рис. 4.40).
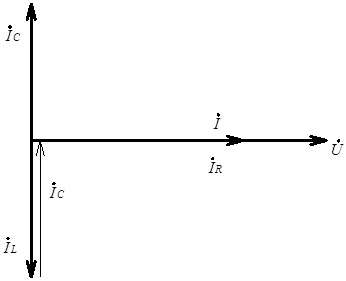
Рис. 4.40. Векторна діаграма струмів електричного кола, в якому спостерігається резонанс струмів
Реактивні провідності відповідних елементів електричного кола на частоті резонансу дорівнюють характеристичній провідності електричного кола й становлять:
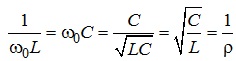 (4.35)
(4.35)
За умови, що характеристична провідність більша за активну провідність резистивного елемента величина струму у реактивних елементах на частоті резонансу перевершує величину струму у нерозгалуженій частині кола. Енергетична сторона процесів, що притаманні резонансу струмів та сама, що й при резонансі напруг.
На рис. 4.41 наведені частотні залежності струмів в елементах електричного кола, в області паралельного резонансу. Як видно, на частоті резонансу струм в такому електричному колі до вузла розгалуження має мінімальне значення. Саме тому при побудові резонансної характеристики електричного кола в режимі резонансу струмів (див. рис. 4.42) для нормування використовується саме це мінімальне значення струму. Із порівняння режимів резонансу напруг та струмів видно, що струми в електричному колі, де спостерігається резонанс струмів, розподіляються аналогічно напругам в електричному колі, де спостерігається резонанс напруг. Тобто ці кола є дуальними.
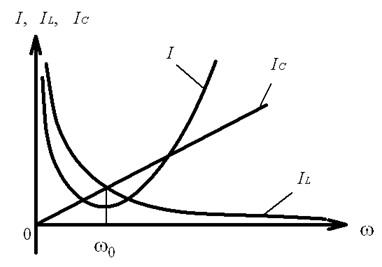
Рис. 4.41. Частотні залежності струмів в елементах електричного кола, в області паралельного резонансу
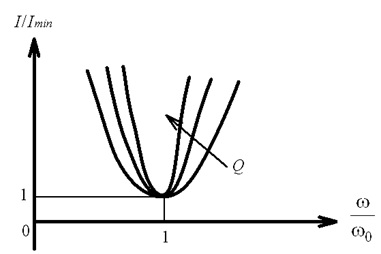
Рис. 4.42. Резонансна характеристика електричного кола режимі резонанса струмів (стрілка вказує напрямок збільшення добротності)
5. Презентація до лекції 4
Для завантаження натисніть сюди: "Презентація до лекції 4".
Шрифти
Розмір шрифта
Колір тексту
Колір тла
Кернінг шрифтів
Видимість картинок
Інтервал між літерами
Висота рядка
Виділити посилання