Тема 2. Метод скінченних елементів. Математичні основи методу скінченних елементів
| Сайт: | Навчально-інформаційний портал НУБіП України |
| Курс: | Програмне забезпечення інженерних розрахунків☑️ |
| Книга: | Тема 2. Метод скінченних елементів. Математичні основи методу скінченних елементів |
| Надруковано: | Гість-користувач |
| Дата: | пʼятниця, 23 січня 2026, 01:42 |
Зміст
- 1. Загальні відомості про метод скінченних елементів.
- 2. Історія розвитку методу скінченних елементів
- 3. Реалізація методу скінченних елементів в сучасних програмних комплексах
- 4. Загальна схема методу скінченних елементів
- 5. Матриця жорсткості скінченного елементу в локальній системі координат
- 6. Матриця перетворень (направляючих косинусів)
1. Загальні відомості про метод скінченних елементів.
Вся історія будівельної механіки в до комп’ютерний період була пов’язана з розробкою прийомів, орієнтованих на чисельну реалізацію тієї або іншої розрахункової схеми. Методи моментних і кутових фокусних відношень, метод Кроса, метод перерозподілу початкових кутових деформацій, метод пружного центру та інші прийоми - ось невеликий перелік з величезного ряду прийомів, що існували у той час, і методів розрахунку конструкцій, які, по суті, зводилися до прагнення уникнути великої кількості обчислень.
І коли фахівець складав розрахункову схему, він перш за все думав про можливість вирішення задачі в такій постановці. Положення докорінно змінилося з появою ЕОМ і методу скінченних елементів.
Метод скінченних елементів (МСЕ) - це чисельний метод вирішення задач прикладної фізики. Ключова ідея методу при аналізі поведінки конструкцій полягає в наступному: суцільне середовище (конструкція в цілому) моделюється шляхом розбиття її на області (скінченні елементи), в кожній з яких поведінка середовища описується за допомогою окремого набору вибраних функцій, що представляють напруження і переміщення у вказаній області. Ці набори функцій часто задаються в такій формі, щоб задовольняти умовам неперервності описуваних ними характеристик у всьому середовищі.
Приклад скінченно-елементної моделі вузла з’єднання елементів металоконструкцій та розподіл нормальних напружень в ньому при навантаженні, отримані за допомогою програмного комплексу ЛІРА- САПР, приведені на рис. 2.1.

Рис. 2.1 Скінченно-елементна модель вузла з’єднання елементів металоконструкцій та розподіл нормальних напружень в ньому
Основні переваги МСЕ:
• легка алгоритмізація при використанні обчислювальної техніки;
• просте формування систем лінійних рівнянь;
• можливість розрахунку неоднорідних і складних конструкцій за різних умов навантаження;
• широкий спектр розв’язуваних задач.
Недоліки МСЕ:
• значний об’єм розрахунків;
• відсутність аналітичного розв’язку (необхідність повного розрахунку схеми для оцінки локального НДС);
• необхідність оцінки точності результатів розрахунку.
2. Історія розвитку методу скінченних елементів
В період з 1850 по 1875 рр. завдяки зусиллям Максвелла, Кастільяно та Мора були вироблені основні концепції теорії аналізу стержневих конструкцій. Ці концепції легли в основу матричних методів будівельної механіки, які остаточно оформилися лише через 80 років і у свою чергу стали основою методу скінченних елементів.
Розвиток теорії і допоміжних дисциплін, що відносяться до методу скінченних елементів, був особливо слабким в період з 1875 по 1920 р. Це відбувалося в основному через наявність реальних труднощів при вирішенні рівнянь лінійної алгебри з великим числом невідомих.
Приблизно до 1920 р. завдяки зусиллям Мейні в США і Остенфельда в Нідерландах були сформульовані основні ідеї чисельного дослідження рамних і фермових конструкцій, засновані на заданні переміщень як невідомих параметрів. Ці ідеї передували сучасним матричним методам дослідження конструкцій, проте важливим стримуючим чинником при аналізі була розмірність задач, що визначалась числом невідомих параметрів переміщень або навантажень.
Ключові ідеї МСЕ в сучасному вигляді прослідковуються в роботах Олександра Хренікова (1941) та Річарда Куранта (1942). Проте, в зв’язку з великою розрахунковою складністю, практичні реалізації методу у формі завершених комп’ютерних програм були створені лише наприкінці 50-х в Штутгартському університеті (Аргеріс), університеті Берклі (Клаф) та університеті Суонсі (Зінкевич, Айронс).
В кінці 50-х - на початку 60-х років з розвитком обчислювальної техніки в будівельній механіці сталася революція, пов’язана з відмовою від багаточисельних вузько орієнтованих прийомів розрахунку. Сталося перенесення центру тяжіння у фундаментальні дослідження методів механіки твердого тіла і математичної фізики, а в інженерній практиці - на прийоми і методи побудови комп’ютерних моделей.
Першою процедурою, яка була реалізована на ЕОМ того періоду, було вирішення систем лінійних рівнянь. Ця процедура, з одного боку, лежить в основі практично всіх чисельних методів, з іншого боку, порівняно проста в реалізації, хоч і пов’язана з великою кількістю обчислень.
Потім було швидко усвідомлено, що можливість вирішення на ЕОМ систем лінійних рівнянь викликає інші проблеми. Складання великих систем і подальша обробка їх розв’язків - обчислення параметрів напружено-деформованого стану - виявилося також дуже трудомістким. Згодом ці процедури також були реалізовані в програмному забезпеченні.
Реалізація інших етапів розрахунку (розрахункові сполучення зусиль, розрахункові сполучення навантажень, підсистеми конструювання та ін.) і їх інтеграція усередині програмних комплексів продовжується і в даний час.
3. Реалізація методу скінченних елементів в сучасних програмних комплексах
Поява ЕОМ зумовила інтенсивну розробку чисельних методів, які, так або інакше, ґрунтувалися на трьох основних методах:
1. Метод сил - основний метод докомп’ютерної епохи, який охоплював можливості різних хитрощів з метою скорочення кількості обчислень (чисельні варіанти розрахункових схем, метод пружного центру та ін.). Незабаром з’ясувалося, що метод сил є неперспективним, зважаючи на труднощі алгоритмізації побудови розрахункових схем, і надалі від нього довелося відмовитися.
2. Варіаційно-різницеві методи - розроблялися для вирішення задач розрахунку пластин і оболонок, ґрунтувалися на методах дискретизації функціоналу потенційної енергії (методи Рітца і Гальоркіна).
3. Метод переміщень - лежить в основі більшості сучасних програмних комплексів скінченно-елементного моделювання, його особливостями є дискретизація пластинчатих систем на основі стержневих апроксимацій та ітераційний (кроковий) метод для вирішення нелінійних задач.
Починаючи з середини п’ятидесятих років МСЕ в своєму розвитку пройшов через ряд безперервних модифікацій. Були сформульовані спеціальні елементи для плоского напруженого стану, введені скінченно-елементні співвідношення для твердого деформованого тіла, пластин, що згинаються, тонких оболонок та інших конструктивних форм. Як тільки були отримані співвідношення для дослідження статичної поведінки лінійно-пружного матеріалу, увага фахівців переключилася на такі аспекти, як динамічна поведінка, геометрична і фізична нелінійності. Услід за цими дослідженнями настав період досить інтенсивного розвитку обчислювальних програм загального призначення, обумовлений бажанням забезпечити практиків можливістю застосовувати вказаний метод.
На сучасному етапі можна виділити три основних напрями розвитку чисельних методів розрахунку конструкцій:
1) пошуки альтернативних МСЕ чисельних методів;
2) вдосконалення МСЕ;
3) вдосконалення програмних комплексів, що реалізують МСЕ.
В 70-80-ті роки розроблялися методи, альтернативні МСЕ в переміщеннях. В основному це методи, засновані на варіаційних формулюваннях, відмінних від функціонала в переміщеннях:
1) метод напружень, в якому використовується функціонал додаткової енергії Кастільяно;
2) змішані та гібридні методи;
3) метод граничних інтегральних рівнянь - дозволяє виразити значення переміщень усередині області через значення на границі, проте непридатний для неоднорідних областей і складної геометрії області.
У зв’язку з тим, що дійсної альтернативи МСЕ в переміщеннях знайти не вдалося, в даний час спостерігається спад в подібних наукових розробках.
Вдосконалення МСЕ в основному було пов’язане з розробкою уточнених типів скінченних елементів (СЕ) з тим, щоб понизити розмірність розв’язуваних рівнянь, а також у застосуванні МСЕ до вирішень задач динаміки, стійкості, фізичної і геометричної нелінійності.
Основні напрями розвитку МСЕ - побудова уточнених СЕ за рахунок збільшення кількості вузлових невідомих і ступенем апроксимуючих поліномів, дослідження впливу одночасного згущування сітки СЕ і збільшення ступеню поліномів на результати моделювання та розробка методів підвищення точності обчислення напружень.
4. Загальна схема методу скінченних елементів
Метод скінченних елементів (МСЕ) ґрунтується на уявному представленні суцільного тіла у вигляді сукупності окремих скінченних елементів, що взаємодіють між собою в скінченному числі точок, які називаються вузлами. Система розбивається на прості скінченні елементи, напружено-деформований стан (НДС) яких попередньо досліджується.
Так, стержневі системи можуть бути розбиті на елементи у вигляді прямолінійних чи криволінійних стержнів з різними умовами з’єднання у вузлах. При розрахунку пластин найчастіше використовуються трикутні або чотирикутні СЕ. Далі будемо розглядати МСЕ розроблений на базі методу переміщень стосовно розрахунку плоских стержневих систем.
Сукупність сполучених між собою і прикріплених до основи СЕ утворює розрахункову схему методу, яку ще називають скінченно-елементною моделлю. Елементи і вузли скінченно-елементної схеми нумеруються.
Зовнішнє навантаження вважається прикладеним тільки у вузлах скінченно-елементної схеми. В загальному випадку при наявності позавузлових навантажень (наприклад, рівномірно розподілених навантажень чи моментів) обов’язково виконується перехід до вузлових навантажень.
У випадку прикладання лише вузлових зовнішніх навантажень переміщення вузлів будь-якого елемента однозначно визначають його внутрішні зусилля і напруження. Зв’язок між переміщеннями вузлів елемента і його внутрішніми зусиллями задається за допомогою матриці жорсткості елементу. Для всіх елементів, з яких складається скінченно-елементна схема, мають бути побудовані матриці жорсткості елементів.
У програмних комплексах, що реалізовують алгоритм МСЕ, зберігаються готові матриці жорсткості для елементів різних типів.
Кількість переміщень вузлів елементу, які однозначно визначають положення цього елементу у просторі називають числом ступенів вільності елемента. Для стержневих елементів плоскої задачі воно визначається за формулою:
n(ст.в.)=2∙n_ш+3∙n_ж (3.1)
де n_ш - кількість шарнірних вузлів в елементі, а n_ж - кількість жорстких вузлів в елементі.
Дійсно, якщо вузол є шарніром, то його положення на площині можна охарактеризувати двома лінійними переміщеннями, наприклад у вертикальному і горизонтальному напрямах. У разі жорсткого вузла необхідно ще додатково до лінійних зміщень задати його поворот.
Аналогічно, для усієї скінченно-елементної схеми вводяться матриця жорсткості системи або глобальна матриця жорсткості, що встановлює зв’язок між переміщеннями вузлів системи і зусиллями в них, а також число ступенів вільності системи - кількість переміщень вузлів системи, які досить знати, щоб однозначно визначити стан усієї системи. Воно також визначається по формулі (3.1), в якій n_ш- число шарнірних вузлів, а n_ж - число жорстких вузлів в усій скінченно-елементній схемі.
Матриця жорсткості системи формується на основі матриць жорсткості всіх елементів схеми в єдиній системі осей координат, яка називається глобальною. При цьому матриці жорсткості окремих елементів формуються в локальних системах координат, що є відмінними від глобальної, і за допомогою спеціальної процедури приводяться до глобальної системи координат. Оскільки матриця жорсткості системи встановлює зв’язок між зусиллями, прикладеними до її вузлів і переміщеннями вузлів, то маючи побудовану матрицю жорсткості системи і знаючи зовнішнє вузлове навантаження, можна знайти переміщення усіх вузлів скінченно-елементної схеми. Для цього потрібно розв’язати систему лінійних алгебраїчних рівнянь. Порядок цієї системи дорівнює числу її ступенів вільності.
Отже, розрахунок стержневої системи МСЕ у формі методу переміщень складається з наступних етапів:
1. Створення скінченно-елементної схеми (розбиття системи на вузли і елементи, їх нумерація, вибір глобальної системи координат).
2. Приведення заданого зовнішнього навантаження до вузлового.
3. Формування матриць жорсткості усіх елементів системи в локальних системах координат і їх перетворення в глобальну систему координат.
4. Формування глобальної матриці жорсткості, складання та розв’язування системи рівнянь МСЕ.
5. Визначення вузлових зусиль в елементах схеми з врахуванням приведеного позавузлового навантаження.
6. Визначення внутрішніх зусиль в елементах схеми, побудова епюр N, Q, M та їх аналіз.
Далі детально розглянемо усі ці етапи.
5. Матриця жорсткості скінченного елементу в локальній системі координат
Матриця жорсткості СЕ в локальній системі координат [r]j’ встановлює зв’язок між одиничними переміщеннями і зусиллями у вузлових точках для горизонтально розташованого елементу.
Як вже відзначалося, основна система МСЕ є сукупністю окремих стержнів, які з’єднуються між собою жорстко або за допомогою шарніра.
Отже, усе різноманіття СЕ можна звести до трьох типів елементів:
а) елемент з двох сторін обмежений жорсткими вузлами: такий елемент має шість ступенів вільності, тобто невідомими є шість можливих переміщень вузлових точок елементу

б) елемент з одного боку обмежений жорстким вузлом, а з іншою шарнірним: такий елемент має п’ять ступенів вільності

в) елемент з двох сторін обмежений шарнірними вузлами: такий елемент має чотири ступені вільності

Розглянемо формування матриць жорсткості для показаних вище трьох типів СЕ у локальній системі осей координат.
Для елементу з шістьма ступенями вільності (тип а) матриця жорсткості матиме вид
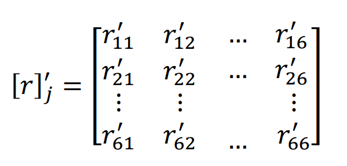 (3.2)
(3.2)
де
r'12- реактивне зусилля в зв’язку 1 від
одиничного переміщення зв’язку 2 і так далі. Чисельні
значення реакцій визначатимемо використовуючи таблиці методу переміщень. Знак
реакцій буде додатнім, якщо напрям реакцій співпадає з додатнім напрямом
переміщень V_j. 1. Формування матриці жорсткості для елементу з шістьма ступенями вільності (тип а) Задамо послідовно одиничні переміщення зв’язкам V_1=l, V_2=1, …, V_6=1. 1)
V_1=1: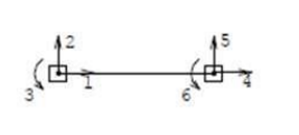

У відповідності із законом Гука:
∆l=Nl/EF, ∆l=V_1=1, N=EF/l
2) V_2=1:
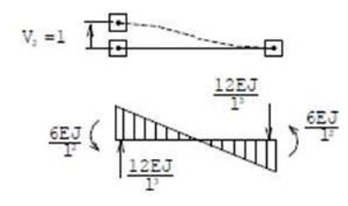
3) V_3=1:
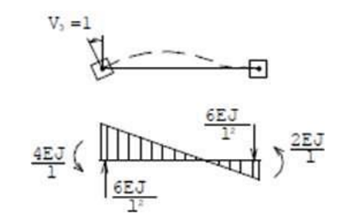
Аналогічно задаємо V_4 = 1, V_5= 1, V_6 = 1.
Розставляючи реакції у відповідні стовпці, отримаємо матрицю жорсткості для елементу з шістьма ступенями вільності
 (3.3)
(3.3)
Запишемо матриці жорсткості для двох інших типів елементів, формуючи їх аналогічно попередній. 2. Матриця жорсткості для елементу з п’ятьма ступенями вільності (тип б) матиме вигляд 3. Матриця жорсткості для елементу з чотирма ступенями вільності (тип в) запишеться (3.4)
(3.4)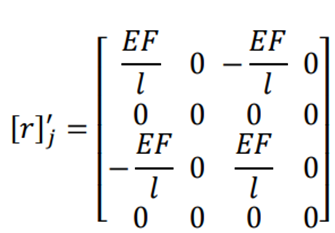 (3.5)
(3.5)
6. Матриця перетворень (направляючих косинусів)
озглянемо тепер СЕ у складі рами, розташований під кутом α до осі X в глобальній системі осей координат. Необхідно перейти від матриці реакцій [r]j в локальній системі координат до матриці [r]j у глобальній системі координат.
Задачу вирішуємо таким чином. На початку побудуємо матрицю [c]j, яка перетворить переміщення СЕ {Z}j в глобальній системі координат в переміщення {V}j:
{V}j= [c]j. {Z}j (3.6)
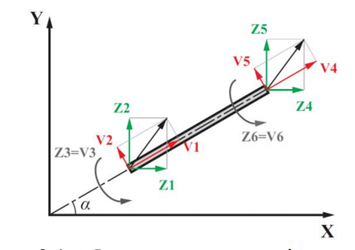
Рисунок 3.1 - Формування матриці перетворень
З рисунку 3.1 запишемо рівняння:
V1 = Z1*cosα+Z2*sinα
V2 = -Z1*sinα+Z2*cosα
V3 = Z3
V4 = Z4*cosα+Z5*sinα
V5 = -Z4*sinα+Z5*cosα
V6= Z6
У матричній формі приведений вище запис матиме вигляд:
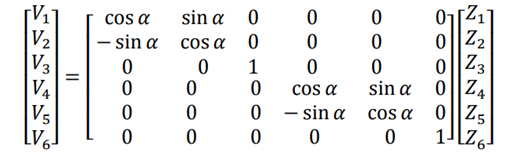 (3.7)
(3.7)
чи у блочній формі
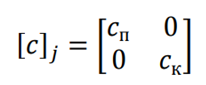
Оскільки ми розглядаємо плоскі пружні системи, то вектори вузлових зусиль і вузлових переміщень, як для окремого елементу, так і для споруди в цілому, пов’язані між собою лінійно:
- в локальній системі координат
{S}j'=[r]j' * {V}j (3.8)
- в глобальній системі координат (основне рівняння МСЕ)
{S}j=[r]j * {Z}j (3.9)
Крім того,
{V}j=[c]j * {Z}j (3.10)
Аналогічно
{S}'j=[c]j.{S}j (3.11)
де {S}'j,{S}j - вузлові зусилля СЕ відповідно в локальній і глобальній системах координат.
Тоді
{S}j = [c]j-1 *{S}j' = [c]j-1 * [r]j' {V}j=[c]j-1* [r]j' * [c]j {Z}j
Для матриці направляючих косинусів виконується рівність [c]j-1= [c]jT. Тоді
{S}j=[c]jT * [r]j' * [c]j * {Z}j
Позначимо
[r]j =[c]jT [r]j' * c]j (3.12)
Вираз (3.12) і є формулою для обчислення матриці жорсткості СЕ в глобальній системі координат.
При формуванні матриць жорсткості окремих елементів [r]j, мають бути зафіксовані початок і кінець кожного стержня, оскільки від цього залежить знак кута а, що визначає орієнтацію стержня в глобальній системі координат XOY.
Шрифти
Розмір шрифта
Колір тексту
Колір тла
Кернінг шрифтів
Видимість картинок
Інтервал між літерами
Висота рядка
Виділити посилання
Вирівнювання тексту
Ширина абзацу