Тема 5. Принципи розрахунку, покладені в основу обчислювальних комплексів
| Сайт: | Навчально-інформаційний портал НУБіП України |
| Курс: | САПР у будівництві |
| Книга: | Тема 5. Принципи розрахунку, покладені в основу обчислювальних комплексів |
| Надруковано: | Гість-користувач |
| Дата: | понеділок, 19 січня 2026, 05:55 |
1. Методи визначення напружено-деформованого стану конструкцій
НДС будівельних конструкцій можна визначити на основі двох рівноцінних напрямків: локального та інтегрального.
Перший базується на розгляді рівнянь будівельної механіки, це рівняння статики, рівняння нерозривності, фізичні та геометричні рівняння. Рівняння локального напрямку подані в таблиці 6.1.
Таблиця 6.1 – Види рівнянь локального методу будівельної механіки
|
Вид рівнянь |
Матричний запис |
Запис з використанням обумовленості про підсумовування Ейнштейна |
|
Статичні (рівняння рівноваги) |
|
де
|
|
Геометричні рівняння нерозривності |
|
де матриці форми; |
|
Фізичні рівняння |
|
де |
Другий напрямок – базується на варіаційному численні, основним поняттям якого є енергія. Енергетичний (термодинамічний) метод вивчення явищ природи розглядає зміни в системі як виділення чи поглинання енергії, перетворення одних видів енергії в інші. Цей метод встановлює загальний напрямок процесів, визначає кінцевий стан, але не дозволяє розглянути протікання процесу.
Енергія – це найбільш загальна кількісна характеристика руху. Внутрішня енергія системи – кількісна форма всіх форм руху, що проявляються при взаємодії внутрішніх елементів системи, утворюючих структуру даного рівня.
В результаті для розв’язання крайових задач із визначення НДС будівельних конструкцій потрібно розв’язувати систему із 15 диференційних рівнянь в частинних похідних з конкретними граничними умовами.
Ця система крайових задач може бути розв’язана числовими методами, оскільки аналітичних розв’язань існує дуже мало:
- методом скінченних різниць (МСР);
- методом скінченних елементів (МСЕ);
- методом граничних елементів (МГЕ).
Дуже багато фізичних явищ зводиться до крайових задач для рівнянь в частинних похідних. Тому область прикладання МСЕ дуже широка. Успішне використання на теперішній час МСЕ пов’язано з таким.
1. Крайові задачі в рівняннях з частинними похідними перетворюються у варіаційні, що дозволяє в рамках прийнятої апроксимації відшукати оптимальне рішення.
2. ЕОМ дозволяє розв’язувати СЛАР високих порядків, а саме до них зводиться пошук розв’язків крайових задач.
3. Стало можливим використання універсальних програм, скрупульозно складених спеціалістами, що дозволяє користувачеві при виконанні великого обсягу розрахунків обмежитись лише підстановкою вхідних даних.
2. Основні положення МСЕ
Проектування будівельних конструкцій (збірних та монолітних) являє собою комплекс розрахунків і графічних робіт із виготовлення транспортування та експлуатації. МСЕ лежить в основі сучасних програмних комплексів таких як: ЛІРА–САПР, SCAD, Robot, які дозволяють виконувати моделювання роботи конструкцій та будівлі в цілому, а також виконувати аналіз їх НДС. Ці програмні комплекси є універсальним інструментом для розрахунків складних споруд із взаємною ув’язкою в конструктивній схемі всіх елементів. МСЕ є числовим, тобто наближеним методом математичної фізики і для його використання необхідно знати основні положення. Числовий МСЕ дозволяє отримувати розв’язки розрахункової системи диференційних рівнянь 15-го порядку (рівняння статики, геометричні рівняння, фізичні рівняння) чи розв’язки задачі знаходження мінімуму функціоналу повної потенціальної енергії шляхом дискретизації розрахункової схеми.
Для отримання розв’язку задачі необхідно:
- визначити фізичні дані про матеріали споруди;
- підібрати розрахункову схему, яка має бути адекватною до споруди;
- вибрати математичну модель – сукупність рівнянь, алгоритмів та їх розв’язків за програмами.
Основний принцип МСЕ – поведінка складного суцільного середовища може бути апроксимована сумарною поведінкою складових елементів цього середовища. Метод скінченних елементів є варіаційним, оскільки його основні розрахункові рівняння можуть бути отримані безпосередньо із варіаційного принципу Лагранжа. Тобто, із множини кінематично-допустимих системою переміщень, що відповідають заданим граничним умовам, ті, які задовольняють вимоги рівноваги, надають потенційній енергії системи стаціонарного значення. В стані стійкої рівноваги величина виразу потенційної енергії системи (функціонал) мінімальна.
На варіаційних методах базується більшість сучасних наближених числових методів, які отримали широке розповсюдження завдяки сучасним ЕОМ. Варіаційні методи мають багато характеристик, найважливіші з них: велика загальність, універсальність, в силу чого наявні широкі можливості для застосування; інваріантність форми подання рівнянь руху; логічна послідовність. В варіаційних методах загальною характеристикою є енергія системи, робота зовнішніх та внутрішніх сил.
На понятті енергії основано багато методів механіки суцільних середовищ, доцільність цих методів базується на тому, що енергія являє собою добре вивчену інваріантну величину і тому не залежить від системи координат.
При застосуванні інтегрального напрямку потрібно знаходити мінімум та максимум функціоналів. В основі розрахункових рівнянь МСЕ лежить класичний варіаційний принцип Лагранжа. Повна потенційна енергія тривимірної системи:
 (6.4)
(6.4)
де U – потенціал деформацій, W – потенціал зовнішніх сил, де перша складова – робота внутрішніх сил; друга складова з від’ємним знаком – робота зовнішніх сил.
Невідомі ступені вільності системи (фізичний зміст яких – лінійні та кутові переміщення) визначаються з умови мінімуму функціоналу повної потенціальної енергії системи
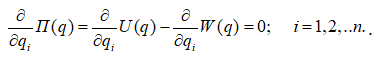 (6.5)
(6.5)
Після диференціювання за кожним ступенем вільності системи отримуємо систему визначальних алгебраїчних рівнянь, яка в математичному вигляді записується так:
 (6.6)
(6.6)
де 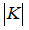 – матриця жорсткості
системи;
– матриця жорсткості
системи;  – вектор ступенів
вільності системи;
– вектор ступенів
вільності системи; 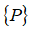 – вектор зовнішніх сил
системи.
– вектор зовнішніх сил
системи.
Дискретизація досліджувальної системи скінченними елементами приводить до виразу:
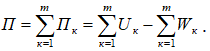 (6.7)
(6.7)
А визначальні алгебраїчні рівняння записуються:
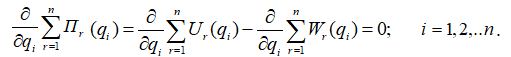 (6.8)
(6.8)
звідки:
 (6.9)
(6.9)
З принципу можливих переміщень елемент матриці жорсткості r-го скінченного елемента:
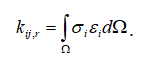 (6.10)
(6.10)
Переміщення по області r-го скінченного елемента:
 (6.11)
(6.11)
Апроксимувальному поліному розподілу переміщень fi
відповідає q-ий
ступінь вільності. Компоненти НДС r-го скінченного елемента:

Інтегральний напрямок опирається на екстремальні принципи, з яких можна отримати розв’язки задач статики, динаміки, стійкості, тобто він є універсальним.
Задачі на пошук мінімуму та максимуму функціоналів – це варіаційні задачі, а набувають функціонали стандартного значення, коли швидкість змінення їх в точці дорівнює нулю, тобто дорівнює нулю перша похідна функціоналу.
Умови, коли функціонали набувають стаціонарного значення,
називаються екстремумами. Нехай на площині маємо 2 зафіксовані точки
А та В (рис. 6.1). Проведемо через них криву у(х) та y(x) , які
відрізняються на нескінченно малу величину, названу Лагранжем
варіацією.

Символ dy запропонований Лагранжем, щоб підкреслити його віртуальний характер. Варіювання означає нескінченно малу зміну функції при фіксованому значенні х. При цьому dx = 0 (що фіксується, та не варіюється). Як відомо, варіювання подібно диференціюванню і при звичайному аналізі функції виконується за тими ж правилами, але не пов’язане з дійсною зміною незалежної змінної. Це свого роду математичний експеримент над сукупністю змінних.
Більшість методів розв’язання варіаційної задачі основано на використанні необхідних умов екстремуму функції, якими є диференційні рівняння плюс граничні умови. Так Ейлер та Лагранж запропонували шукати екстремальні значення функціоналів, перейшовши до розв’язання крайової задачі
 (6.14)
(6.14)
де у – невідома шукана функція; F – повна потенційна енергія одиниці довжини системи – тобто робота зовнішніх і внутрішніх сил системи при переході її із деформованого стану в початковий недеформований; – нескінченно мала величина; f (x) задовольняє умови неперервності та диференційованості.
Оскільки розв’язання крайової задачі (6.14) в більшості практичних випадків приводить до значних математичних ускладнень, варіаційні методи замість розв'язку диференційних рівнянь в частинних похідних розв’язують деяку задачу мінімізації, в якій згідно з методом Рітца шукана функція апроксимується найкраще підібраним аналітичним виразом.
В методі Рітца суттєвим є підбір підходящої базисної функції, яка б задовольняла кінематичні граничні умови і близько апроксимувала дійсний обрис осі чи поверхні. При цьому розрахунковим диференційним рівнянням координатна функція може не задовольняти. Точність методу Рітца в основному залежить від того, наскільки точно вибрані для апроксимації базисні функції відповідають дійсній деформованій осі чи поверхні.
Виявляється, що функція (екстремаль), яка забезпечує мінімум виразу повної потенційної енергії роботи (функціоналу) є в той же час розв’язком вихідного диференційного рівняння в частинних похідних (2.14).
Розрахунок за МСЕ розпочинається з дискретизації розрахункової схеми. Кожний скінченний елемент зберігає всі фізичні та геометричні властивості вихідного середовища і є елементом скінченних розмірів: стержень для одновимірних об’єктів, для дво- чи тривимірних об’єктів теорії пружності це трикутні чи чотирикутні скінченні елементи, тетраедри. На границі області задаються граничні умови, реактивні сили чи переміщення. Саме подання в МСЕ скінченних елементів кінцевих розмірів дає можливість перейти від реальної схеми з нескінченним числом параметрів НДС до системи з кінцевим числом параметрів.
Розрахункова схема МСЕ. Дискретизація об’єкта.
Спрощене зображення реальної споруди, яке присутнє в розрахунку замість самої споруди, є розрахунковою схемою. Як відмітив проф. Ю. В. Верюжський, основними принципами створення розрахункових моделей споруд є такі положення:
- методи розрахунку мають витікати із форм руйнування і деформацій, підтверджених досвідом будівельної практики;
- розрахункова гіпотеза має ставити конструкцію в менш прийнятні умови, ніж ті, в яких дійсно знаходиться конструкція;
- набір розрахункових гіпотез має забезпечувати не лише міцність та стійкість, а і економічність конструкції;
-доцільно мати не одну модель, а систему апроксимувальних моделей роботи споруди, кожна з яких має свої межі застосування;
- апроксимувальна модель роботи споруди має не лише правильно відображати роботу реального об’єкта, але й бути настільки простою, щоб розрахунок не був занадто громіздким [Ошибка! Источник ссылки не найден.].
Компонування розрахункової схеми – це завжди компроміс. Розрахункову схему споруд компонують із стержнів, пластин, оболонок (завдяки їх вивченості це дає можливість передбачати їх поведінку). Спрощене, ідеалізоване зображення реальної системи, що присутнє в розрахунку замість самої системи – це розрахункова схема.
Вона складається із:
- геометричної схеми елементів конструкції (стержень, пластина, оболонка, масивне тіло), які описані в бібліотеці скінченних елементів з відомими їм базисними функціями, типами вузлових невідомих);
- прикладеного навантаження (розподіленого, зосередженого);
- опорних закріплень (зв’язків з землею, шарнірних чи жорстких);
- модельного середовища (усереднені фізико-механічні показники, які характеризують модельне середовище і для нього вже можна застосовувати математичний аналіз).
При переході від реального матеріалу до його модельного середовища використовують гіпотези суцільності та однорідності.
Розрахункова схема відрізняється від самої споруди вилученням несуттєвих особливостей. Етап вибору розрахункової схеми найважливіший. До методів схематизації відносяться: ідеалізація матеріалу у вигляді суцільного однорідного середовища; подання елементів будівлі у вигляді набору стандартних скінченних елементів (СЕ) – стержнів, пластин чи оболонок, поєднаних вузлами; ідеалізація форми зовнішніх сил.
Наступним є етап опису скінченно-елементної моделі будівлі у формі, придатній до розрахунку. Компоновці скінченно-елементної моделі споруди із «елементарних частинок» відповідає набір СЕ – із бібліотеки скінченних елементів конкретного програмного комплексу.
Всі СЕ та вузли розрахункової схеми нумеруються через необхідність робити на них посилання. Розв’язування проводиться енергетичним методом з використанням варіаційного обчислення.
Розв’язати задачу в варіаційній постановці – це значить знайти таку систему переміщень, яка доставить мінімум функціоналу повної потенціальної енергії системи.
Як прийнято в варіаційних методах, шукані функції переміщень наближено подають в вигляді набору компонентів (в вигляді координатних функцій):
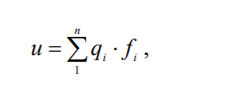 (6.15)
(6.15)
В результаті введення такого роду апроксимації функціонал повної потенціальної енергії системи стає скінченно-вимірною функцією із ступенями вільності qi (і = 1, 2, 3 .. n). Ступені вільності визначаються із умови мінімуму функціонала повної потенційної енергії, тобто варіаційного рівняння Лагранжа

Елементи правої частини (6.18) по суті є
вузловими навантаженнями (реактивними зусиллями), тобто навантаженнями, до яких прикладено місцеві навантаження, розподілені по області системи,
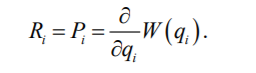 (6.19)
(6.19)Лівою частиною (6.18) буде добуток lkl *{q{
Тоді:
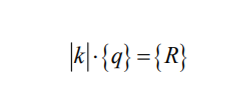 (6.20)
(6.20)
буде розрахунковим рівнянням МСЕ. В фізичному змісті його можна трактувати як рівняння рівноваги. Елементи матриці жорсткості kij– це зусилля, що виникають у напрямку і-го ступеня вільності від j-го одиничного переміщення за умови, що всі решта (і ≠ j) ступені вільності qi = 0 .
Як відомо, серцевиною математики є алгоритми, а решта – зручні поняття, доведення теорем про їх властивості. Алгоритмом розв’язування задач за МСЕ є така послідовність:
- побудова функціонала;
-дискретизація системи на СЕ і вибір координат функції;
-побудова матриці жорсткості kij та зведення місцевого навантаження до вузлового для кожного СЕ;
- побудова канонічних рівнянь;
- розв'язування СЛАР;
- визначення компонентів НДС по області СЕ.
На прикладі, взятому із практики реального проектування, відслідковано всі етапи інформаційних технологій розрахунку конструкцій: аналіз прийнятих конструктивних рішень, компоновка адекватних розрахункових схем, скінченно-елементне моделювання, реалізація обчислень в середовищах сучасних програмних комплексів, візуалізація результатів. Послідовність дій при визначенні НДС розрахункової схеми за МСЕ розглянемо на прикладі плоскої рами на рис. 6.2.
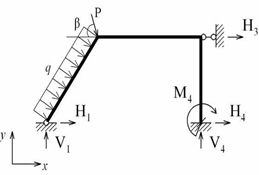
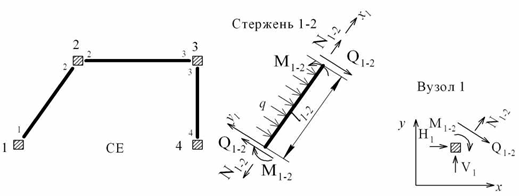
Рисунок 6.2 – Скінченно-елементна модель плоскої рами
Взаємодію системи з довкіллям подають, зазвичай, у вигляді навантажень або впливів, прикладених до вузлів системи (вузлових навантажень) чи до внутрішніх точок її скінченного елемента (місцевих навантажень). Місцеві навантаження можуть бути силами чи моментами, зосередженими чи розподіленими по стержнях, площинах чи об’ємах, інколи завантаження системи подається у вигляді температурних впливів на СЕ або заданими зміщеннями у вузлах, тобто ці впливи подаються не як силові, а як кінематичні фактори. При розв’язанні задач необхідно шукати такі сполучення зовнішніх впливів (РСЗ), що призводять до найбільш небажаних наслідків.
Для мінімізації похибки, що залежить від послідовності нумерації вузлів, доцільно проводити цю нумерацію, починаючи із найбільш піддатливої частини конструкції, поступово переміщуючись до місць її закріплення.
Проста двовимірна задача є зручною відправною точкою для подальших викладень, оскільки вона дозволяє проілюструвати всю послідовність дій для конкретного числового прикладу. В тривимірному випадку об'єм обчислень вельми великий, він значно зростає. Вхідну інформацію щодо об’єкта, який розраховується, можна розділити на три типи:
1 – геометрична (топологічна інформація про координати вузлів, системи і зв'язок між вузлами);
2 – фізична інформація (жорсткість поперечних перетинів);
3 – завантаження системи (вектор {F} зовнішніх навантажень). Потрібно визначити:
- зусилля у всіх стержнях (вектор {S});
-переміщення усіх вузлів системи (вектор {Δ}).
Отже, відомі – {F}, невідомі – {s}, {Δ}.
Для розв’язання задачі потрібно побудувати:
- матрицю умов рівноваги |А| (матрицю форми);
-матрицю піддатливості |D| та обернену до неї матрицю жорсткості |К| =|D|-1.
Компонування рівнянь рівноваги. Рівняння рівноваги: |К| {s}={F}. Стержнева система складається із скінченних елементів: стержнів та вузлів. Сукупність рівнянь рівноваги, складених для кожного стержня і вузла може розглядатись як система умов рівноваги усієї стержневої системи.
Рівняння рівноваги для вузлів доцільно записувати, використовуючи загальну систему координат усієї системи. При складанні цих рівнянь рівноваги для стержнів виявляється зручним обирати для кожного стержня свою власну систему координат – місцеву або локальну х'; y'; початок системи координат установлювати у вузлі з меншим номером. Види вузлів, з'єднання декількох стержнів та реакції, що в них виникають, подано на рис. 2.3.

Далі: вузол 2, стержень 2-3, вузол 3, стержень 3-4, вузол 4.
Коефіцієнти перед невідомими із складених умов рівноваги записуємо в таблицю 6.2, в якій компонується матриця умов рівноваги |А| та вектор зовнішнього навантаження {B}.
Компонування геометричних рівнянь. Внаслідок виникнення внутрішніх зусиль стержні деформуються, а вузли переміщуються. Проте стержні не відокремлюються один від одного. Тобто стержні деформуються сумісно і узгоджено, залежно від переміщень їх кінців, які являють собою вузли стержневої системи.
Таблиця 6.2 – Компонування матриці форми A та вектора
зовнішнього навантаження {B} для 24 невідомих схеми рами на рис. 6.2
|
N 1-2 |
Q 1-2 |
M 1-2 |
N 2-1 |
Q 2-1 |
M 2-1 |
V1 |
H1 |
N 2-3 |
Q 2-3 |
M 2-3 |
N 3-2 |
Q 3-2 |
M 2-3 |
V4 |
Вільні члени (вектор зовнішньог о навантаж. F) |
|
-1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
1 |
0 |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
q l1-2 |
|
0 |
0 |
1 |
0 |
l1-2 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
-(q l1-2)/2 |
|
cosα |
sinα |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
sinα |
cosα |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |


Розглянемо стержень на рис. 6.4.

Рисунок 6.4 – Одновимірний скінченний елемент
Кожний вузол "і" має три компоненти:
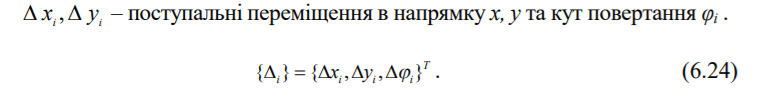

Між статичними та геометричними рівняннями існує певний зв'язок. Передусім, використовуючи матрицю рівноваги А однієї категорії, можна записати рівняння іншої категорії. Це набагато полегшує складання геометричних рівнянь, оскільки геометричні дослідження споруд становлять чималі труднощі, а складання рівнянь рівноваги здійснюється порівняно просто. Тобто, між рівняннями рівноваги та геометричними існує правило подвійності – умовам однієї системи відповідають змінні іншої системи і навпаки.
3. Компонування фізичних рівнянь
Фізичні рівняння:
D {S} = {e}. (6.25)
Розрахункова стержнева схема складається із вузлів, які
з'єднані між собою лінійними СЕ, що
називаються стержнями. У лінійно-деформованих
об'єктах між вузловими
реакціями і вузловими
переміщеннями, що їх зумовлюють, існує лінійна залежність (6.20)R = K D
, де K – матриця жорсткості (матриця пружності), що визначає лінійний зв'язок між векторами напружень s та векторами деформацій , s = k e (закон Гука),де k – це вузлова
реакція, що викликана
вузловим переміщенням умови
що всі інші переміщення дорівнюють нулю. Розглянемо навантажений стержень
i-j рис. 6.5. Рисунок 6.5 – До побудови
матриці піддатливості для стержневого СЕ Для знаходження Kij потрібно почергово надавати одиничні переміщення вузлам дискретної моделі і знаходити
сили, які при цьому передаватимуться на вузли. Матриця
жорсткості K є оберненою до матриці піддатливості D . Деформацію стержня {e} характеризує три компоненти:φ,φ,l, які можна визначити Переміщення δij можна знайти за відомими формулами Максвелла Мора Систему (2.26)
можна подати в матричному вигляді: Коли знехтувати поздовжніми деформаціями l Якщо стержнів в системі "n"
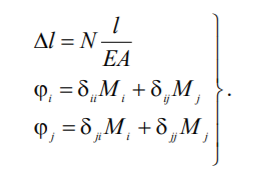 (6.26)
(6.26) (6.27)
(6.27)
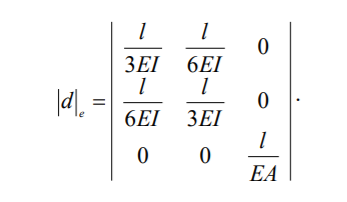 (6.29)
(6.29) (6.30)
(6.30) (6.31)
(6.31)
Шрифти
Розмір шрифта
Колір тексту
Колір тла
Кернінг шрифтів
Видимість картинок
Інтервал між літерами
Висота рядка
Виділити посилання
Вирівнювання тексту
Ширина абзацу
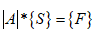
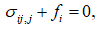 (6.1)
(6.1)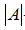
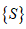 – вектор шуканих зусиль;
– вектор шуканих зусиль; 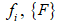 – вектор
зовнішніх навантажень.
– вектор
зовнішніх навантажень.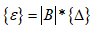
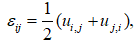 (6.2)
(6.2)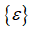 –вектор деформацій;
–вектор деформацій; 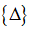 – вектор переміщень;
– вектор переміщень; 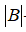 – матриця градієнтів, похідна від
– матриця градієнтів, похідна від 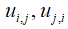 – похідні від переміщень.
– похідні від переміщень.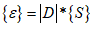
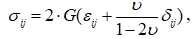 (6.3)
(6.3)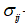 – тензор напружень;
– тензор напружень;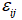 – тензор деформації;
– тензор деформації;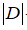 – матриця піддатливості;
– матриця піддатливості;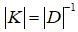 – матриця
жорсткості;
– матриця
жорсткості;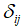 – дельта Кронекера.
– дельта Кронекера.