Тема 8. Нелінійні розрахунки будівельних конструкцій
| Сайт: | Навчально-інформаційний портал НУБіП України |
| Курс: | САПР у будівництві |
| Книга: | Тема 8. Нелінійні розрахунки будівельних конструкцій |
| Надруковано: | Гість-користувач |
| Дата: | середа, 14 січня 2026, 09:06 |
1. Загальна характеристика нелінійних розрахунків.
Раніше розглядалося рішення тільки лінійних задач – тобто таких, в яких зв’язок між силами, що діють на конструкцію, і переміщеннями її точок приймається лінійним, а в основі фізичних рівнянь, як правило, лежить узагальнений закон Гука. Насправді це часто не відповідає дійсності. Наприклад, бетон, дерево, пластик і деякі інші будівельні матеріали характеризуються нелінійною залежністю напруже від деформацій навіть при невеликих навантаженнях. Така нелінійність називається фізичною. Проявляється вона при виникненні пластичних деформацій, при криволінійній діаграмі «напруження- деформації», при зміні властивостей матеріалів від зовнішніх впливів і т. д.
При значних переміщеннях, співрозмірних з розмірами конструкції, необхідно враховувати геометричну нелінійність, наприклад, в разі поздовжнього і поздовжньо-поперечного згину стержнів, зміні координат точок конструкції через порівняно великі переміщення.
Особливе місце займає конструктивна нелінійність, пов’язана зі зміною розрахункової схеми конструкції в процесі навантаження (врахування односторонніх зв’язків): при контактній взаємодії деформівних тіл (односторонні опори, тріщини), при розрахунку конструкцій типу вант, з затяжками і т. п.
Класифікація та характеристики основних типів задач наведені на рис. 8.1, узагальнене порівняння характеристик лінійного та нелінійного розрахунків приведено в табл. 8.1.
Завдання розрахунку несучих конструкцій, орієнтовані на уточнене прогнозування особливостей поведінки системи на усіх етапах її роботи, включаючи етапи, що передують руйнуванню, найчастіше не можуть бути вирішені методами лінійної будівельної механіки. Відхилення від закону Гука (фізична нелінійність), відмова від розгляду умов рівноваги в геометричних термінах недеформованого стану (геометрична нелінійність), врахування можливої зміни розрахункової схеми в процесі деформування (конструктивна нелінійність) складають звичайний «набір нелінійностей».

Рисунок 8.1 – Класифікація та характеристики основних типів задач
Цей набір далеко не повний. Він не включає розгляд ефектів, що виникають при протіканні процесів реологій в матеріалі (наприклад, повзучість) і нелінійні ефекти опору руху типу сухого тертя або іншої природи, крім того він опускає нелінійності, пов’язані з накопиченням напружень і деформацій в процесі зміни конструкції при її створенні (генетичну нелінійність). Останній тип нелінійності, звичайно можна розглядати, як варіант конструктивної нелінійності, оскільки розглядаються системи зі змінною розрахунковою схемою, але тут зміни відбуваються не в результаті дії навантаження, а цілеспрямовано, за задумом проектувальника, що дає підстави для її окремого розгляду і найменування.
Особливо слід застерегти користувача програмних засобів, де представлена «фізична нелінійність». Річ у тому, що в багатьох з них розглядається задача, що відрізняється від лінійної тільки тим, що функціональна лінійна залежність між напруженнями і деформаціями замінена деякою нелінійною функцією. При цьому така функція приймається однозначною і однаковою для навантаження і розвантаження. Проте такі нелінійно-пружні матеріали в природі майже не зустрічаються, а відхилення від закону Гука у більшості конструкційних матеріалів пов’язані з явищами пластичності. Але реальний пластичний матеріал після розвантаження дає залишкові деформації.
Приведене вище зауваження часто парирується посиланням на те, що розглядатимуться тільки такі історії поведінки конструкції, коли усі навантаження тільки зростають. Але річ у тому, що зростання навантажень не гарантує росту напружень в усіх точках тіла, тому, навіть прийнявши таке самообмеження, не можна себе застрахувати від помилки.
Таблиця 8.1 – Порівняння лінійного та нелінійного розрахунків
|
Характеристика |
Лінійні задачі |
Нелінійні задачі |
|
Залежність переміщень від навантаження |
Лінійно залежність |
Нелінійна залежність |
|
Зв’язок між напруженнями та деформаціями |
Лінійна залежність |
Нелінійна залежність напружень від деформацій або часу |
|
Величина переміщення |
Зміни геометрії через переміщення вважаються малими та ігноруються при перевірці рівноваги |
Переміщення можуть бути не малими, для перевірки рівноваги використовують деформований стан |
|
Властивості матеріалу |
Лінійні пружні властивості, які просто визначаються |
Нелінійні властивості, часто невідомі, що потребує проведення додаткових експериментальних досліджень |
|
Зворотність деформацій |
Всі деформації повністю зворотні і зникають при розвантаженні системи |
Після зняття навантаження стан системи може відрізнятися від вихідного |
|
Граничні умови |
Під час розрахунку залишаються незмінними |
Можуть змінюватися (наприклад, змінюються площадки контакту). |
|
Послідовність прикладання навантажень |
Не важлива, результуючий стан від неї не залежить |
Стан конструкції може залежати від послідовності прикладання навантажень |
|
Час виконання обчислень |
Менший, ніж при нелінійному розрахунку |
Приріст навантаження та ітерації потребують значного часу, особливо при високій ступені точності |
|
Використання результатів |
Результати розрахунку на різні навантаження допускають додавання та домноження на деякі коефіцієнти з метою отримання розрахункових сполучень |
Розклад задачі на складові впливи і наступне об’єднання результатів неможливе |
|
Вихідний напружено- деформівний стан |
Вихідний НДС неважливий |
Вихідний НДС потрібно задати |
2. Розв’язування систем нелінійних рівнянь.
Розрахунок нелінійних систем є більш складним завданням в порівнянні з рішенням лінійних задач, оскільки тут доводиться враховувати деформований стан розглянутої області, відмовитися від принципу незалежності дії сил, застосовувати спеціальні методи пошуку і аналізу рішення. При цих умовах отримати аналітичний розв’язок задачі, як правило, не вдається, тому розрахунок виконується за допомогою чисельних методів, найчастіше МСЕ, використовуючи при цьому процедури послідовних наближень.
Методи, що розглядаються нижче, часто застосовуються для вирішення нелінійних задач. Усі вони засновані на лінеаризації нелінійних рівнянь, тобто пошук розв’язку нелінійних рівнянь здійснюється розв’язуванням рекурентної послідовності лінійних. Деякі з них порівняно мало відомі (метод послідовних жорсткостей), хоча у ряді випадків досить ефективні.
Розглянуті методи можна розділити на два класи:
1) ітераційні, для яких відома точність рішення, але невідома кількість обчислень (ітерацій), які знадобляться, щоб досягти задану точність:
- метод пружних розв’язків (рис. 8.2, а) – загальна матриця жорсткості представляється як сума лінійної та нелінійної складових;
- метод змінних жорсткостей (у математиці він відомий як метод січних, рис. 8.2, б) – загальна матриця жорсткості і-ї ітерації визначається на основі переміщень (і-1) ітерації;
- метод Ньютона-Рафсона (рис. 8.2, в) – на кожній ітерації визначається поправка на основі відхилення вузлових сил;
- метод Ньютона-Канторовича (рис. 8.2, г) – модифікований м-д Ньютона-Рафсона без перерахунку матриці жорсткості на кожній ітерації.
2) прямі, для яких заздалегідь відома кількість обчислень, але невідомо, яка буде досягнута точність. Сюди відносяться крокові методи:
- метод послідовних жорсткостей;
- метод послідовних навантажень з урахуванням нев’язок.
Відомі також і інші модифікації крокових методів. Більшість модифікацій крокових методів пов’язана з уточненням рішення на кожному або на наступних кроках.
Крокові методи знайшли дуже широке застосування, і це, разом з достатньо легкою реалізацією, пояснюється також можливістю організації комп’ютерного моделювання процесу навантаження або процесу зміни напружено-деформованого стану конструкції в часі, викликаного таким чинником, як повзучість.
При необхідності вирішення тільки нелінійної задачі, тобто визначення напружено-деформованого стану, відповідного заданому навантаженню, перевагу слід віддавати ітераційним методам. При необхідності проведення математичного моделювання процесу навантаження використовуються крокові методи.
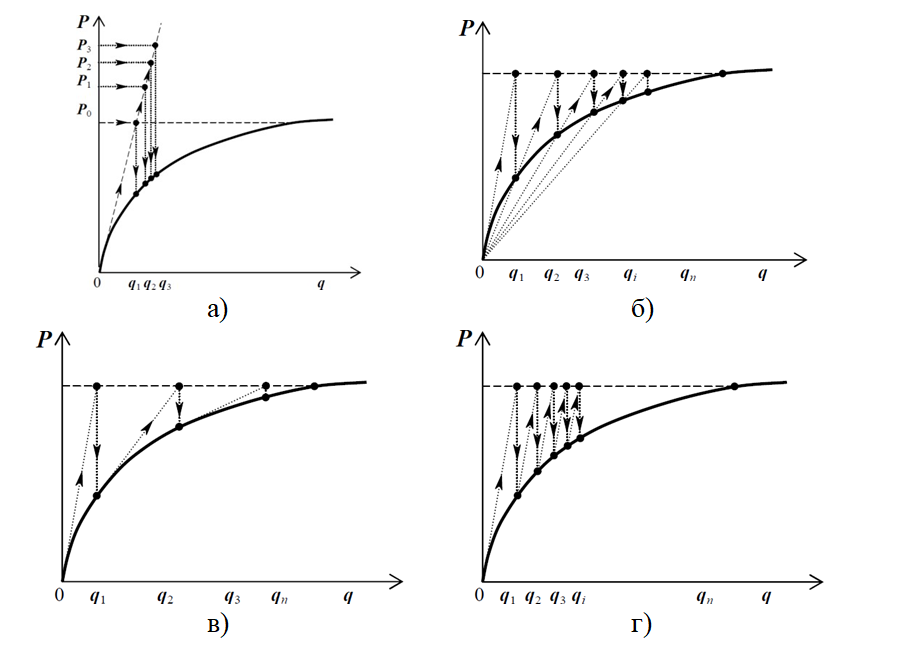
Рисунок 8.2 – Графічна інтерпретація ітераційних методів розрахунку
3. Кроковий метод.
Відомі декілька варіантів крокової процедури, які відрізняються лише використовуваними методами чисельного рішення задачі Коші. Усі вони випробувані на практиці і мають свою сферу застосування. Так, в ПК ЛІРА є можливість використовувати наступні модифікації крокового методу:
- простий кроковий метод;
- кроковий метод з уточненнями;
- кроково-ітераційний.
У першому випадку на кожному кроці вирішується лінеаризована задача, і в припущенні, що це рішення є досить точним, реалізується перехід до наступного кроку навантаження (рис. 8.3, а). Погрішність розв’язку нелінійної задачі не контролюється – передбачається, що погрішність мала за рахунок вибору малого кроку чисельного інтегрування.
Другий варіант передбачає контроль нев’язок на кожному кроці та ітераційне уточнення навантаження чергового кроку за рахунок врахування нев’язки в рівняннях рівноваги (рис. 8.3, б).
Нарешті, в третьому випадку виробляється ітераційне уточнення рішення на кожному кроці з коригуванням лінеаризованої матриці жорсткості на кожній ітерації (рис. 8.3, в).
Важливою особливістю крокової процедури і її привабливою відмінністю від інших методів рішення нелінійних рівнянь є те, що лінеаризована в околі деякого навантаження система може аналізуватися звичайними методами лінійної будівельної механіки. Мають сенс оцінки коефіцієнта запасу стійкості або частоти і форми власних коливань такої лінеаризованої системи.
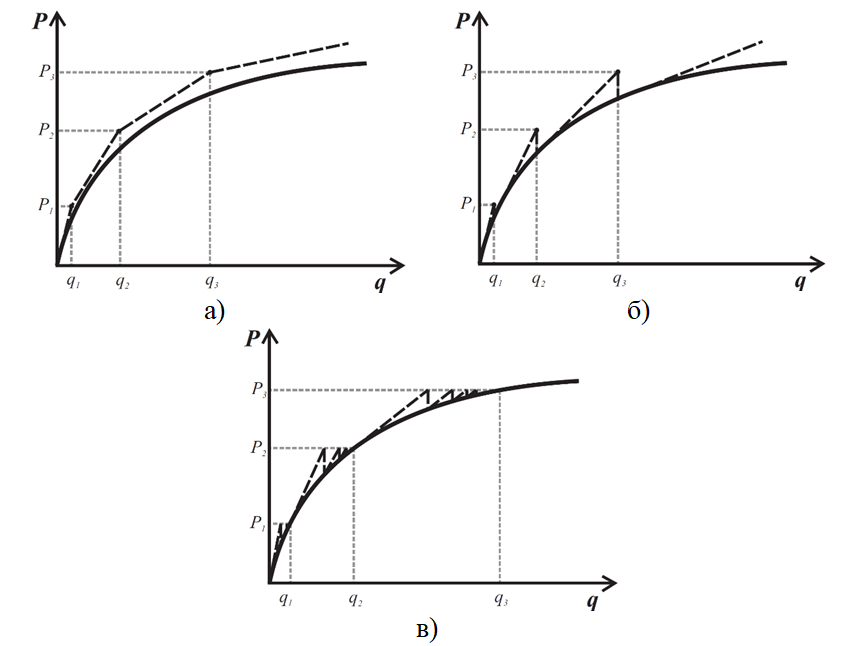
Рисунок 8.3 – Графічна інтерпретація крокових методів розрахунку
Необхідно відмітити, що дослідження поведінки нелінійної системи може вимагати перегляду прийнятої раніше розрахункової схеми, зокрема, збільшення деталізації скінченно-елементної сітки.
Для вирішення фізично і геометрично нелінійних завдань будівельної механіки кроковим методом в ПК ЛІРА призначений кроковий процесор ЛІР- СТЕП. Він організовує кроковий процес і забезпечує рішення лінеаризованої системи дозволяючих рівнянь на кроці для поточного приросту вектора вузлових навантажень, сформованого для конкретного навантаження.
Кроковий процесор дозволяє отримати напружено-деформований стан з урахуванням нелінійних ефектів як для мономатеріальних, так і для біматеріальних (залізобетон) систем. Для біматеріальних систем пропонується певний набір типів армуючих включень.
Матриця жорсткості лінеаризованої фізично нелінійної системи формується на основі змінних інтегральних жорсткостей, що отримуються в точках інтегрування скінченного елементу при вирішенні пружної задачі на конкретному кроці. Схема чисельного інтегрування по області скінченного елементу і набір використовуваних жорсткостей визначаються типом скінченного елементу. Для отримання відповідного набору інтегральних жорсткостей переріз скінченного елементу в точках інтегрування дробиться на ряд елементарних підобластей, в центрах яких визначаються нові значення фізико-механічних характеристик матеріалу, відповідно до заданої користувачем діаграми деформування матеріалу. На кожному кроці вирішується лінеаризоване завдання з формуванням векторів переміщень, зусиль і нових інтегральних жорсткостей із дотичного модуля для наступного кроку. Кількість кроків і коефіцієнти до навантаження задаються користувачем. В цьому випадку основне рівняння МСЕ має вигляд
[K (u)]{u} = {P} (8.1)
де [K (u)] – матриця жорсткості, яка перераховується на кожному кроці з врахуванням поточного значення модуля пружності матеріалу.
ЛІР-СТЕП дозволяє комбінувати лінійні і нелінійні скінченні елементи, а також реалізовувати розрахунок за суперелементною схемою, якщо нелінійні елементи присутні тільки в основній схемі.
Для задання параметрів нелінійності у всіх діалогових вікнах задання характеристик жорсткості для стандартних перерізів додається група кнопок
«Врахування нелінійності», які стають активними після задання відповідного типу скінченних елементів.
Шрифти
Розмір шрифта
Колір тексту
Колір тла
Кернінг шрифтів
Видимість картинок
Інтервал між літерами
Висота рядка
Виділити посилання
Text Alignment
Paragraph Width