Тема 10.1 Розрахунки з врахуванням геометричної та конструктивної нелінійності
| Сайт: | Навчально-інформаційний портал НУБіП України |
| Курс: | САПР у будівництві |
| Книга: | Тема 10.1 Розрахунки з врахуванням геометричної та конструктивної нелінійності |
| Надруковано: | Гість-користувач |
| Дата: | пʼятниця, 27 лютого 2026, 06:45 |
1. Геометрична нелінійність
У геометрично нелінійних завданнях нелінійною є залежність між переміщеннями і деформаціями , крім того , при застосуванні принципу можливих переміщень необхідно враховувати зміну геометрії схеми.
Виділяють наступні 4 ієрархічних рівні геометрично нелінійних постановок завдань для скінченно вимірних систем:
1). До першого рівня геометричної нелінійності віднесемо слабкий варіант геометрично нелінійних теорій. У цьому варіанті теорії вважається , що рівняння рівноваги слід записувати для деформованого стану системи. Що стосується звязку деформацій з переміщеннями , то ці співвідношення для першого рівня геометрично нелінійних завдань приймаються в лінійному варіанті. У будівельній механіці завдання першого рівня геометричної нелінійності іноді називають розрахунком за деформованою схемою.
2).Для другого рівня геометричної нелінійності вводиться нелінійна залежність між переміщеннями та деформаціями. Істотним тут є розрізнення порядків малості деформацій і поворотів, при цьому вважається, що квадрати кутів поворотів елементів даної розрахункової схеми є величинами того ж порядку малості , що і компоненти деформацій , які у свою чергу , набагато менші за одиницю. Малі в порівнянні з одиницею і сам повороти.
ε<<1 , ϒ<<1 (10.1)
3). До третього рівня геометричної нелінійності можна віднести завдання , в яких деформації малі в порівнянні з одиницею , тоді як відносно кутів поворотів таких припущень зробити не можна. Конструкції з гнучкими нитками служать відмінним прикладом завдань цього рівня геометричної нелінійності.
ε<<1 , ϒ˜1 (10.2)
4). Для четверного рівня геометричної нелінійності самі відносні деформації не можна вважати малими величинами в порівнянні з одиницею, наприклад при проведенні розрахунків виробів з гуми і подібних матеріалів.
ε˜1 , ϒ˜1 (10.3)
2. Універсальний стрижневий скінченний елемент геометрично нелінійної задачі.
Універсальний стрижневий скінченний елемент геометрично нелінійної задачі (тип СЕ 310) орієнтований на забезпечення розрахунку усіх видів стрижневих систем з врахуванням геометричної нелінійності і по архітектурі є аналогом універсального лінійного стержневого скінченного елементу для лінійної задачі (тип СЕ 10).
Для врахування геометричної нелінійності стержня вважається, що виконується закон Гука (σ = Eε), а деформація, що входить в цей вираз, має наступний вигляд:
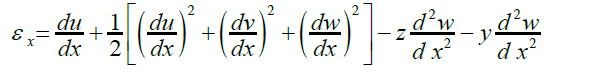 (10.4)
(10.4)
Для коректного розв’язування задач, що містять геометрично нелінійні СЕ необхідно проводити досить дрібне розбиття стержнів між точками опори, оскільки побудова епюр проводиться по приведеному у вузли схеми навантаженню і тому на кожному із стержнів епюри будуть лінійними.
Бібліотека геометрично нелінійних СЕ містить елементи, що дозволяють проводити статичний аналіз конструкцій з урахуванням геометричної нелінійності стержнів, плит, оболонок та об’ємних тіл. Для моделювання геометричної нелінійності використовуються CE №300-399 з бібліотеки СЕ ПК ЛІРА, а СЕ з №400-499 одночасно володіють властивостями фізичної та геометричної нелінійності.
3. Конструктивна нелінійність. Односторонні зв’язки.
Даний клас задач враховує зміну розрахункової схеми в процесі навантаження – виникнення нових в’язей чи усунення існуючих.
Діапазон можливих переміщень в цьому випадку задається односторонніми в’язями – елементами, які працюють тільки на розтяг або тільки на стиск. Математично описуються умовами-нерівностями для переміщень.
Системи, де обмеження на переміщення визначені умовами-нерівностями (односторонні в’язі) зустрічаються частіше, ніж про це звично думають. Конструкція, вільно оперта на деяку поверхню, котра забороняє переміщення у бік цієї поверхні і не перешкоджає переміщенню в протилежному напрямі, гнучкі нитки, які дозволяють зближуватися своїм кінцевим точкам і не дозволяють їм віддалятися більш ніж на довжину нитки є простими прикладами (рис 10.1). Типовими прикладами можуть також служити: кам’яна кладка, виконана насухо, зв’язок між фундаментом споруди і ґрунтом, що його підстилає. Сипучі ґрунти або абсолютно гнучкі мембрани можуть служити прикладами складніших систем з односторонніми в’язями.
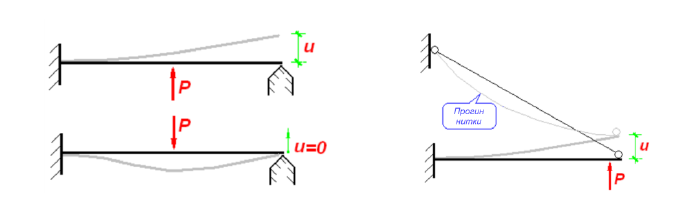
Рисунок 10.1 – Приклади конструктивної нелінійності
За традицією, такого роду в’язі розглядають як ідеальні двосторонні, перевіряючи апостеріорно чи не порушує отримане рішення характер роботи в’язей. Ця традиція склалася давно, коли вручну отримати рішення для правильно сформульованого завдання було досить складно, зараз же практично будь-який сучасний програмний комплекс такі завдання вирішує в правильній постановці.
Моделювання конструктивної нелінійності проводиться з допомогою одно- та двохвузлових СЕ односторонньої в’язі (СЕ №251, 252, 255, 256), які можуть знаходитися в одному з двох станів – робочому (в’язь включено) чи неробочому (в’язь виключено). Дані СЕ дозволяють врахувати нелінійність в’язей між вузлами розрахункової схеми або нерівність границь податливості в’язі в прямому і протилежному напрямах, коли граничне зусилля розтягу не рівне граничному зусиллю стиску.
Шрифти
Розмір шрифта
Колір тексту
Колір тла
Кернінг шрифтів
Видимість картинок
Інтервал між літерами
Висота рядка
Виділити посилання
Вирівнювання тексту
Ширина абзацу