Тема 3. Результати розрахунку конструкцій методом скінченних елементів
| Сайт: | Навчально-інформаційний портал НУБіП України |
| Курс: | Програмне забезпечення інженерних розрахунків☑️ |
| Книга: | Тема 3. Результати розрахунку конструкцій методом скінченних елементів |
| Надруковано: | Гість-користувач |
| Дата: | пʼятниця, 23 січня 2026, 01:41 |
1. Матриця жорсткості для споруди в цілому.
Розглянемо тепер як формується матриця жорсткості для споруди в цілому, коли є матриці жорсткості для усіх окремих елементів. Нехай задана яка-небудь стержнева система (рис. 3.1).

Рисунок 3.1 – Стержнева система
Усі вузли вважатимемо жорсткими, тобто з кожним з них пов’язано по 3 можливі переміщення.
Матрицю жорсткості для всієї споруди покажемо у блочному виді, з розмірами блоків 3х3, оскільки з кожним вузлом пов’язано по 3 можливі переміщення (горизонтальне, вертикальне і поворот вузла).
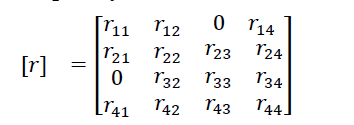 (3.1)
(3.1)
Тут r12 – перший індекс вказує номер вузла, в якому виникає блок реакцій, а другий – номер вузла, змішенням якого ці реакції викликані. Нульові блоки означають, що відповідні вузли не пов’язані безпосередньо стержнем і прямо не взаємодіють, тобто не передають реакції з вузла у вузол.
Загальна матриця жорсткості [r] виходить шляхом сумування відповідних блоків матриць жорсткості окремих стержнів. Наприклад, перший рядок блочної матриці [r] отриманий шляхом сумування відповідних блоків матриць жорсткості окремих елементів:
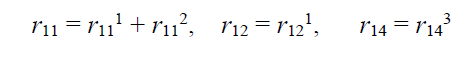 (3.2)
(3.2)
2. Визначення переміщень і зусиль в елементах схеми.
З основного рівняння МСЕ (3.9) визначається вектор вузлових переміщень
{Z} = [r]-1{S} (3.3)
Таким чином стають відомими переміщення всіх вузлів розрахункової схеми. Внаслідок нерозривності деформацій скінченноелементної моделі кінці стержнів, що примикають до вузлів, які переміщуються, матимуть такі самі переміщення. Отже, для кожного стержня скінченноелементної моделі можна побудувати вектор вузлових переміщень в локальній системі {S}j′.
Сумарні реакції на кінцях стержня складаються з реакцій, які зумовлені переміщеннями вузлів скінченноелементної моделі і силами, що спричинені дією прикладеного на стержні зовнішнього навантаження. Дія сумарних кінцевих реакцій зумовлює внутрішні зусилля на кінцях стержня. Приклавши сумарні кінцеві реакції до стержня в локальній системі координат, можемо обчислити внутрішні зусилля в будь-якому його перерізі, розглядаючи рівновагу однієї з його частин.
3. Приклад розрахунку рами методом скінченних елементів.
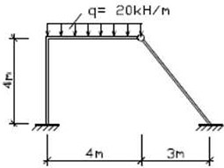
Порядок розрахунку рами МСЕ розглянемо на конкретному невеликому прикладі. Задана рама показана на рис. 3.2 а). Жорсткості EA1 = EA3 = 10 МН, EA2 = 20 МН, EI1 = 1 МН/м2, ЕІ2=2 МН/м2.
 а)
а) 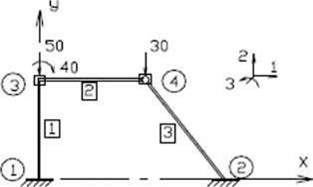 б)
б)
Рисунок 3.2 – Задана рама (а) і основна схема МСЕ (б)
Основну систему МСЕ вибираємо розбиваючи раму на три прямолінійні скінченні елементи (СЕ). Нумеруємо вузли та елементи.
У вузлі 3 елементи з’єднуються між собою жорстко, з цим вузлом пов’язано три невідомі переміщення. У вузлі 2 елементи з’єднуються шарніром, тут два невідомі переміщення. У опорних вузлах 1 і 2 усі три переміщення дорівнюють нулю. Отже, дана рама має п’ять невідомих переміщень в МСЕ. Додатні напрями переміщень і зовнішніх навантажень приймаємо як показано на малюнку.
Глобальну систему осей координат розташовуємо так, щоб координати усіх вузлів були додатними. Розподілене по ригелю навантаження приводимо до вузлового, використовуючи для цього таблиці методу переміщень (рис. 3.3).
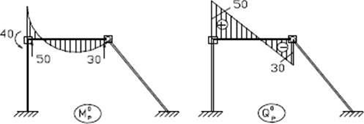
Рисунок 3.3 – Приведення позавузлового навантаженням до вузлового
Складаємо початкові матриці. Вектор зовнішніх навантажень Р для споруди в цілому в загальній системі осей координат і вектори перетворень позавузлових навантажень до вузлових для СЕ в локальних системах координат S 0 мають вигляд
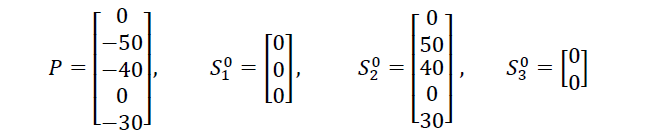
Матриці жорсткості для СЕ в локальній системі координат складаються таким чином. Матриця жорсткості для першого елементу має розмірність 3x3. оскільки три переміщення пов’язані з вузлом 1 рівні нулю, тому з матриці для елементу з двома жорсткими вузлами (3.3) викреслюємо три перші рядки і три перші стовпці. Для другого елементу матриця жорсткості має розмірність 5x5 та вигляд (3.4). Для третього елементу переміщення у вузлі 2 також рівні нулю, тому його матриця жорсткості матиме розмірність 2x2 на основі (3.4). Локальна система координат пов’язана з окремим елементом, вісь X спрямована уздовж стержня від початкового вузла до кінцевого, а вісь Y нормально до неї.

Матриці направляючих косинусів, мають ту ж розмірність, що й матриці жорсткості : для першого елементу 3x3, для другого 5x5, для третього 2x2. Поворот елементів здійснюється проти годинникової стрілки, навколо початкового вузла з горизонтального положення до положення як в конструкції. У нашому випадку φ1=90°, φ2=0°, φ3=127°. Матриці направляючих косинусів запишуться
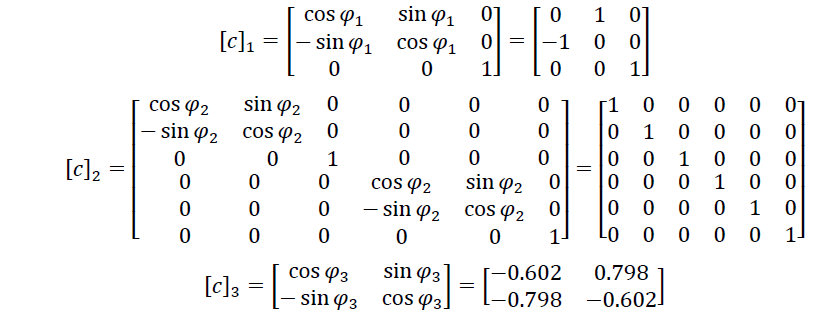
Матриці жорсткості окремих елементів в глобальній системі координат обчислюють за формулою
[r]j = [c]jT [r]j′ [c]j.
Після перемножування відповідних матриць, отримуємо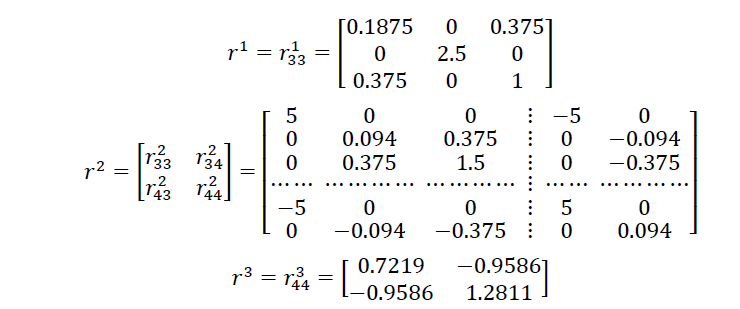
Матриця жорсткості споруди в цілому формується з блоків матриць жорсткості окремих елементів таким чином:
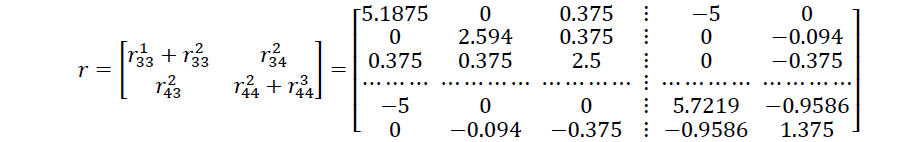
де r331 – блок реакцій, що виникають за рахунок пружних властивостей першого елементу, в зв’язках накладених на третій вузол, від одиничних зміщень цих же зв’язків.
Після знаходження оберненої матриці [r]-1 по відомих стандартних процедурах, вектор переміщень Z визначається по формулі

Вектори вузлових зусиль в стержнях в загальній системі координат обчислюємо за формулою
Sі = rі Zі
В результаті обчислень маємо:
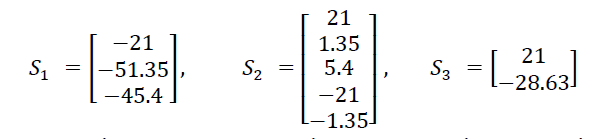
Зусилля у вузлах скінченних елементів в локальній системі координат з врахуванням векторів перетворень навантажень визначаються
Si′ = ci Si + Si0 (3.4)
У нашому випадку в результаті обчислень маємо
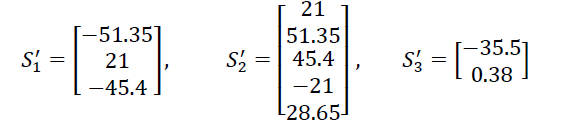
Маючи вектори зусиль в локальній системі координат, прикладаємо їх до відповідних вузлів окремих елементів і будуємо епюри внутрішніх зусиль (рис. 3.4).
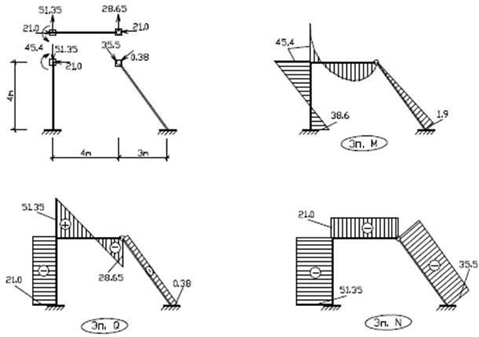
Рисунок 3.4 – Епюри внутрішніх зусиль
Для виконання статичної перевірки, покажемо розрахункову схему рами із заданими навантаженнями і опорними реакціями. Напрями і величини опорних реакції визначаємо по епюрах.
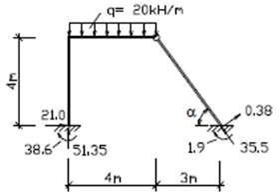
Рисунок 3.5 – Схема рами з визначеними опорними реакціями
Тоді умови статичної рівноваги записуються як:
ΣX = 0: 21 + 0.38sinα – 35.5cosα = 0
ΣY = 0: 51.35 + 0.38cosα + 35.5sinα = 0
ΣMB = 0: q∙4∙5 – 51.35∙7 – 38.6 – 35.5 = 0
Шрифти
Розмір шрифта
Колір тексту
Колір тла
Кернінг шрифтів
Видимість картинок
Інтервал між літерами
Висота рядка
Виділити посилання
Вирівнювання тексту
Ширина абзацу