Тема 4. Принципи побудови скінченно-елементних моделей
| Сайт: | Навчально-інформаційний портал НУБіП України |
| Курс: | Програмне забезпечення інженерних розрахунків☑️ |
| Книга: | Тема 4. Принципи побудови скінченно-елементних моделей |
| Надруковано: | Гість-користувач |
| Дата: | пʼятниця, 23 січня 2026, 01:36 |
1. Системи координат.
Сучасні програмні комплекси надають користувачеві можливість використання набору різних систем координат. Можна виділити три основні види
систем координат (рис. 4.1):
- Глобальна (X, Y, Z) – відносно якої може описуватися весь набір чинників, що характеризують комп’ютерну модель: вузлові переміщення, в’язі місцеві і вузлові навантаження, напруження і т. д. Глобальна система координат може бути декартовою, циліндричною, сферичною і ін.
- Місцева система координат (X1, Y1, Z1) є прерогативою скінченних елементів. Відносно неї може задаватися навантаження, що діє по області скінченного елементу, обчислюється напруження, ведеться розрахунок армування.
- Локальна система координат (X2, Y2, Z2) є прерогативою вузлів. Відносно неї можуть задаватися напрями переміщень, вузлові навантаження, в’язі.
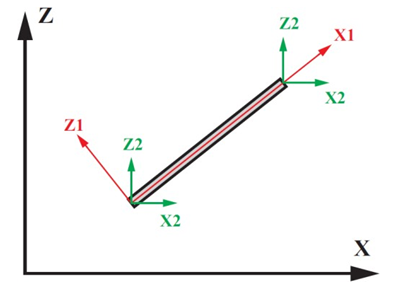
Рисунок 4.1 – Системи координат стержневого СЕ
2. Ознаки схеми.
Кожний вузол схеми в загальному випадку має 6 ступенів вільності: три лінійні переміщення вздовж осей X; Y; Z і три повороти навколо X; Y; Z. Для розрахункових схем, у яких кількість ступенів вільності у вузлі менша шести (плоскі ферми, плоскі рами і т.п.), для зменшення розмірності задачі застосовується так звана ознака схеми. В ПК ЛІРА-САПР задіяні п’ять ознак схеми:
Ознака 1 – схеми, що розташовуються в площині XOZ; кожний вузол має 2 ступені вільності – лінійні переміщення уздовж осей X, Z. За цією ознакою розраховуються плоскі ферми і балки-стінки.
Ознака 2 – схеми,
що розташовуються в площині XOZ; кожний вузол має 3 ступені вільності – лінійні переміщення уздовж осей X, Z і
поворот навколо осі Y. За цією
ознакою розраховуються плоскі рами і допускається включення елементів ферм
і балок-стінок. Ознака 3 – схеми, що розташовуються в площині XOY; кожний вузол має З ступені вільності – лінійне переміщення
вздовж осі Z і навколо осей X, Y. За цією ознакою розраховуються балочні ростверки і плити; допускається врахування пружної основи. Ознака 4 – просторові схеми, кожний вузол яких має 3 ступені вільності – лінійні
переміщення уздовж осей X, Y, Z. За цією ознакою
розраховуються просторові
ферми та об’ємні тіла. Ознака 5 – просторові схеми загального виду з шістьма
ступенями вільності у вузлі. За цією ознакою
розраховуються просторові каркаси,
оболонки і допускається включення об’ємних
тіл, врахування пружної
основи і т.п.
3. Моделювання шарнірів у стержневих і площинних елементах.
Під словом «шарнір» мається на увазі звільнення від лінійної або кутової в’язі між вузлом схеми і кінцем стержня, що входить у цей вузол, чи вузлом скінченного елемента
У стержнях шарніри задаються безпосередньо при створенні схеми і орієнтуються відносно осей місцевої системи координат Х1, Y1, Z1. Шарнірне кріплення стрижня до вузлів може бути реалізоване також за допомогою нульової згинної жорсткості.
При заданні шарнірів у площинних елементах рекомендується використовувати такий прийом: у місці, задання шарніра здійснити подвійну нумерацію вузлів розбиття (один із вузлів відноситься, до одного, а інший – до іншого скінченного елемента). Потім об’єднати відновідні лінійні переміщення цих вузлів. Якщо в іншому напрямку шарнір відсутній, то об’єднуються також і кутові переміщення цих вузлів у цьому напрямку.
Якщо необхідно, наприклад, у плиті (рис. 4.2) описати шарнір відносно осі Y, то по лінії вузлів 4, 12, 20, 28, 36 робиться подвійна нумерація вузлів (додаються вузли. 5, 13, 21, 29, 37, координати яких можуть співпадати з координатами вузлів 4, 12, 20, 28, 36). Потім попарно об’єднуються (для вузлів 4 і 5, 12 і 13 і т.д.) переміщення у напрямках Z і UX. Для елементів оболонок, крім цього, попарно об’єднуються лінійні переміщення вузлів у напрямках X і Y.
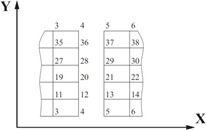 Рисунок 4.2 – Моделювання шарніру у плиті
Рисунок 4.2 – Моделювання шарніру у плитіТак само чинять при шарнірному кріпленні елементів оболонки до стержня. Окремо нумеруються вузли оболонки і стержня (та ж подвійна нумерація), а потім попарно об’єднуються переміщення вузлів у напрямках X,Y і Z.
Якщо відомі лінійні податливості в місці установки шарніра, то між вузлами подвійної нумерації задається пружна в’язь (СЕ типу 55). У цьому випадку об’єднання переміщень по вказаних напрямках не задається.4. Врахування прямої та косої симетрії.
Якщо розрахункова схема має площини симетрії, то для зменшення розмірності задачі рекомендується вводити у розрахунок частину схеми, що обмежена цими площинами.
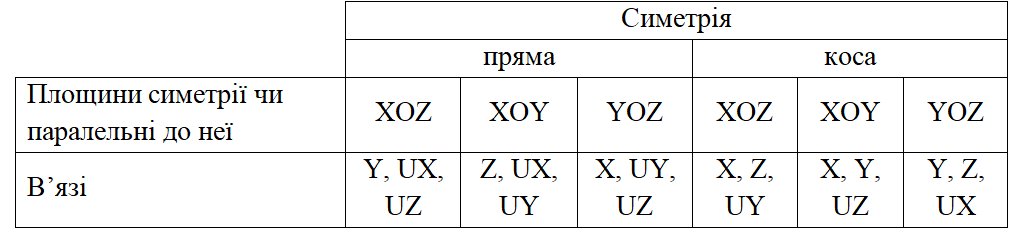
На вузли, що лежать у площині прямої симетрії, накладаються в’язі, ортогональні до цієї площини, а при косій симетрії – паралельні до неї. У табл. 4.1 показано, за якими напрямками ступенів вільності на ці вузли накладаються в’язі.
Якщо площина симетрії не паралельна до жодної з площин загальної системи координат, то накладання відповідних в’язей можна виконати за допомогою локальної системи координат вузла.
Таблиця 4.1 – Накладання в’язей при врахуванні симетрії.
Шрифти
Розмір шрифта
Колір тексту
Колір тла
Кернінг шрифтів
Видимість картинок
Інтервал між літерами
Висота рядка
Виділити посилання
Вирівнювання тексту
Ширина абзацу