Тема 5. Раціональне розбиття на скінченні елементи
| Сайт: | Навчально-інформаційний портал НУБіП України |
| Курс: | Програмне забезпечення інженерних розрахунків☑️ |
| Книга: | Тема 5. Раціональне розбиття на скінченні елементи |
| Надруковано: | Гість-користувач |
| Дата: | пʼятниця, 23 січня 2026, 01:36 |
1. Принцип фрагментації конструкції.
Іноді доводиться розв’язувати великі задачі, в яких густу сітку застосувати не можна через обмежені ресурси комп’ютера, а укрупнене розбиття не дає достатньої картини напружено-деформованого стану конструкції. У цьому випадку пропонується поєднати укрупнену і густу сітку.
Фрагментацією називають виділення з конструкції деякої її частини для подальшого розрахунку лише цієї виділеної частини конструкції (фрагмента). Взаємодія фрагмента з рештою конструкції замінюється дією силових або деформаційних чинників в місцях примикання відкинутої частини. Звичайно, значення цих чинників беруться з розрахунку всієї конструкції, схема якої може бути достатньо спрощеною, зате сам фрагмент може бути скільки завгодно складний, і мати навіть інший тип скінченно-елементної моделі. Наприклад, загальна схема може бути стержневою, а фрагмент досліджуваного вузла може бути створений на основі тривимірних скінченних елементів.
Фрагментація полягає у послідовному вирізуванні та детальному розрахунку якоїсь певної частини конструкції. Такий підхід застосовується при дослідженні областей концентрації напружень – навколо отворів, у місцях різкої зміни перерізів елементів і т.д. Його можна застосовувати також при розв’язуванні великих задач. Спочатку розраховується схема з укрупнених скінченних елементів. Потім вирізаються окремі фрагменти цієї схеми і розбиваються детальніше. Розрахунок фрагменту здійснюється на впливи, отримані в результаті розрахунку крупної схеми.
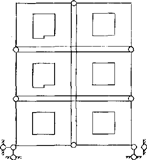
Так, для багатоповерхової будівлі (рис.5.1) найважливішою інформацією є картина напружено-деформованого стану перших трьох поверхів. Тут можна виконати густе розбиття лише перших трьох поверхів. Розбиття решти поверхів може бути досить грубим.
 Рисунок 5.1 – Приклад
фрагментації для багатоповерхової будівлі
Рисунок 5.1 – Приклад
фрагментації для багатоповерхової будівлі
2. Суперелементне моделювання.
У ПК ЛІРА-САПР реалізована можливість роботи із суперелеменгною розрахунковою моделлю. На кількість невідомих не накладається ніяких обмежень. Вибір розбиття схеми на суперелементи або лише на скінченні елементи залишається за користувачем.
При використанні суперелементної моделі конструкції основна розрахункова схема розбивається на декілька розрахункових схем, які називаються схемами суперелементів. Вузли стикування суперелементів з основною схемою називаються супервузлами.
Якщо ж у схемі є одинакові суперелементи, то кількість обчислень можна істотно скоротити, якщо виконати всі обчислення для одного з них і отримані результати використати для решти суперелементів цього ж типу. Такий підхід справедливий і у тому випадку, коли суперелементи одного типу по-різному орієнтовані щодо глобальної системи координат основної схеми.
Зрозуміло, всі ці переваги суперелементної моделі повною мірою проявляються лише у тому випадку, коли в системі є багато однакових суперелементів, що повторюються, в яких кількість внутрішніх вузлів помітно перевищує число зовнішніх вузлів.
Використовуючи суперелементи, можна провести розрахунок поетапно, істотно понизивши на кожному етапі розмірність завдання. Спочатку будують матрицю жорсткості для всіх типів суперелементів, потім розраховують систему, що складається з суперелементів. В результаті цього розрахунку визначають переміщення супервузлів. На заключному етапі розраховують кожен з суперелементів на задані переміщення супервузлів.
Використання суперелементів доцільне у таких випадках:
- передбачувана розмірність задачі при скінченно-елементному розбитті перевершує можливості комп’ютера (пам’ять, швидкодія, погана обумовленість матриці);
- у задачі міститься велика кількість ідентичних конструктивних елементів (панелі, об’ємні блоки і т.п.);
- наявні типові конструктивні елементи, які вже були сформовані для об’єктів, що були розраховані раніше;
- є локальне зосередження елементів, що нелінійно деформуються.
Бувають випадки, коли задача містить декілька різних об’єктів, що відрізняються матеріалами, набором скінченних елементів, геометрією і т.п. Наприклад, при розрахунку панельних будинків дрібне розбиття кожної панелі призводить до великої розмірності задачі, а застосування суперелементів дозволяє істотно знизити вплив розмірності подібних задач на швидкість їх виконання (рис. 5.2). При цьому варто врахувати й те, що кількість типів суперелементів у таких задачах, зазвичай, невелика.
 а)
а) 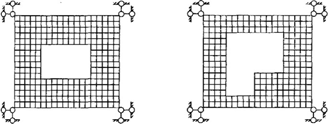 б)
б)
Рисунок 5.2 – Діафрагма багатоповерхової будівлі (а) та відповідні їй типи
Істотного скорочення часу розрахунку можна досягти при розв’язуванні нелінійних задач, у яких наявні крупні включення, що лінійно деформуються. Наприклад, складні будівлі, що опираються на пружну основу. Для таких будівель врахування нелінійної роботи основи має істотне значення. У цьому випадку наземну будівлю необхідно оголосити суперелементом, матриця жорсткості якого на кожному кроці нелінійного розрахунку залишається незмінною.
Теоретично суперелементи у свою чергу можна розбивати на підсхеми (суперелементи 2-го рангу), розвиваючи цей процес і організовуючи своєрідну багаторангову рекурсію. У ПК ЛІРА реалізований лише один ранг суперелементів. У переважній більшості випадків цього достатньо для описання розрахункової схеми дуже високої розмірності.
Використання суперелементів корисне не лише для зменшення розмірності вирішуваного завдання, але і для зручності синтезу і аналізу.
3. Об’єднання переміщень.
У ПК ЛІРА-САПР передбачена можливість задання інформації про вузли, що мають однакові переміщення у заданому напрямку. Ці переміщення одержують один порядковий номер, тобто відбувається об’єднання декількох невідомих у системі лінійних алгебраїчних рівнянь.
Об’єднання переміщень різних вузлів схеми, тобто примусове нав’язування значень переміщень одного вузла іншому, є широко поширеним прийомом при створенні розрахункових схем. Цей прийом використовується найчастіше для того, щоб змоделювати нехтування деякими деформаціями системи.
Наприклад, такий прийом дозволяє об’єднувати горизонтальці переміщення вузлів, що належать перекриттю в плоских багатоповерхових рамах, адже перекриття являють собою жорсткий диск: поздовжня сила, що може виникнути в перекритті, дуже мала в порівнянні з перерізом перекриття, що її сприймає. Дуже зручний такий прийом у задачах з динамічними впливами від вітру чи сейсміки в горизонтальному напрямку. У цьому випадку інерційна маса всього перекриття збирається в один (будь-який) вузол перекриття.
Складніше об’єднувати переміщення в просторі по поверхах перекриття. Для симетричної багатоповерхової рами, наприклад, можна нехтувати закручуванням її навколо вертикальної осі. Тоді достатньо об’єднати переміщення всіх вузлів перекриття у напрямках X,Y, і схема в цьому випадку спрощується.
Для випадків, коли центр жорсткості будівлі не співпадає з центром мас, а також для несиметричних в плані будівель (особливо при недостатній кількості діафрагм жорсткості) закручуванням будівлі нехтувати не можна. Тут потрібно об’єднувати горизонтальні переміщення на рівні перекриття по рамах. Якщо вважати, що диск перекриття не може змінювати своєї форми, то необхідно об’єднати переміщення для всього перекриття по повороту ще й відносно осі Z.
4. Абсолютно жорсткі вставки.
Абсолютно жорсткі вставки використовуються, як правило, при порушенні співвісності стикування стержнів у вузлі (стик частин колони, примикання до колони ригелів різної висоти, врахування ребр в плитах і т.п.).
Жорсткі вставки орієнтуються уздовж осей місцевої системи координат Х1, Y1, Z1. Навантаження, що задаються на стержень з жорсткими вставками, прив’язуються до початку пружної частини. Заданий шарнір розташовується між жорсткою вставкою і пружною частиною. Зусилля обчислюються тільки в пружній частині, тому при перевірці рівноваги у вузлі, де є такий стрижень, слід здійснювати перенос зусиль з пружної частини у вузол з урахуванням заданого навантаження на вставку.
При розрахунку стержневих систем часто виникає необхідність врахувати ексцентричність стиковки елементів у вузлах (рис. 5.3). Вставка між вузлами n і n+1 стержня з дуже великою, але скінченною жорсткістю, як це представляється інтуїтивно можливим, призводить до різкої втрати точності обчислень за рахунок погіршення обумовленості матриці жорсткості. Для обходу цієї обчислювальної трудності в розрахункових комплексах передбачається можливість використовувати нескінченно жорсткі вставки по кінцях стержневих елементів. Тоді розрахункова схема має лише один вузол, що займає довільне положение на прямій між вузлом n і вузлом n + 1. Втрата точності в цьому випадку не спостерігається.
Найпростіше можна поступити, якщо цей єдиний вузол сумістити з вузлом n або n + 1, тоді абсолютно жорстка вставка з’явиться лише в одного з елементів. Платою за це спрощення є те, що внутрішні сили будуть визначені лише на пружній частині стержня.
Якщо є абсолютно жорсткі в’язі, що не співпадають з напрямком осей загальної системи координат, то вони реалізуються за допомогою локальної системи координат вузла.
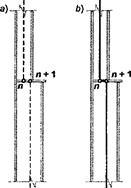 Рисунок 5.3 – Ступінчастий стик колони
Рисунок 5.3 – Ступінчастий стик колони
Якщо діафрагма жорсткості має відношення Н/а > 6, то її доцільно замінити стержнем еквівалентної жорсткості, а для включення цього стержня використовувати абсолютно жорсткі вставки. На рис. 5.4, а показане застосування цього прийому для фрагмента рамно-в’язевої системи у випадку, якщо діафрагма не має отворів, а на рис. 5.4 б показаний цей же прийом, якщо діафрагма має отвори.
У ряді випадків така заміна може призвести до точнішого розв’язку, ніж скінченно-елементна модель. Якщо елемент має невелике відношення поперечних розмірів до довжини, то його моделювання скінченними елементами вимагає дуже густої сітки, а моделювання стержнем у цьому випадку є доцільнішим.
а)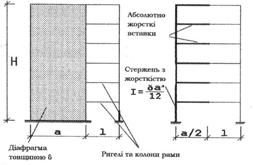 б)
б)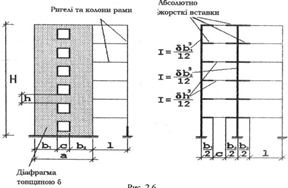
Рисунок 5.4 – Заміна діафрагми жорсткості стержнем
5. Сполучення різних типів скінченних елементів.
Лише у окремих випадках вся конструкція представлена елементами одинакового типу (наприклад, лише елементами плити); частіше зустрічаються випадки, коли в одній розрахунковій моделі присутні і стержневі, і оболонкові, і інші елементи.
Сучасні розрахункові програмні комплекси допускають майже довільну комбінацію скінченних елементів найрізноманітніших типів, розмірності, розмірів і геометричної форми, а також з різними чисельними характеристиками жорсткості, проте при їх використанні необхідно враховувати особливості сполучення різних типів скінченних елементів.
Сполучення колон і плит
За останні роки популярними стали розрахунки стержневих каркасів будівель і споруд спільно з плитними фундаментними конструкціями.
Розглянемо дискретну розрахункову схему, що поєднує в собі скінченні елементи плити і стержневі елементи, жорстко приєднані до плити. Сітка скінченних елементів плити вибирається так, щоб стержні каркаса будівлі потрапляли у вузли сіткового розбиття плити. Якщо не робити жодних додаткових заходів, то описана вище розрахункова схема у вузлах стиковки плитних і стержневих елементів забезпечить спільність як вертикальних переміщень плити і каркасу (переміщень в напрямі, перпендикулярному площині плити), так і відповідних кутів повороту. Проте, отримувані в цій розрахунковій схемі згинні моменти в перетинах стійок, що примикають до плити, не мають відношення до дійсного розподілу внутрішніх зусиль.
Починаючи з деякої сіткової розбивки, подальше дроблення сітки повинне призводити до зменшення абсолютних значень згинних моментів в стержнях в місцях їх закладення в плиту. У границі, при прямуванні максимального розміру сіткового елемента до нуля ці згинні моменти також повинні прямувати до нуля, а це означає, що дана розрахункова схема забезпечує не жорстке, а шарнірне приєднання елементів каркаса до плити. Те, що користувач формально при вибраній їм сітці набуває деяких відмінних від нуля чисельних значень згинних моментів свідчить лише про погрішність дискретизации в методі скінченних елементів.
Для того, щоб відкоректувати розрахункову схему, слід розглянути конструктивне рішення в місці прикріплення каркаса до плити. Якщо стійки каркаса приєднані до плити за допомогою підколонників, то останні можуть розглядатися як абсолютно жорстке тіло, що не міняє своїх розмірів при будь-яких змінах сітки скінченних елементів плити. Розміри ж абсолютно жорсткого тіла можна призначити, виходячи з розмірів підколонника (а х b) з врахуванням розподілу тиску від нього на плиту під кутом 45° (рис. 5.5) до серединної поверхні плити, що повністю відповідає традиційній інженерній практиці.
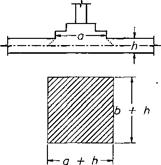 Рисунок 5 .5 – Сполучення колони з плитою через підколонник
Рисунок 5 .5 – Сполучення колони з плитою через підколонник
У цій схемі зосереджений момент від стійок каркаса передається на плиту через жорстку шайбу, розміри якій а+h і b+h не зв’язані з розмірами сітки скінченних елементів, а значить, і з погрішністю дискретизації. Хоча погрішність дискретизації і впливатиме на чисельні значення згинних моментів в стійках, вона не надасть такої катастрофічної дії на відхилення розрахункової схеми від реальної конструкції, як це було у вихідній постановці завдання без введення в розрахункову схему жорсткого тіла. У тому випадку, коли підколонники відсутні, можна в якості розмірів жорсткого тіла прийняти розміри поперечного перетину стійки.
Опирання плити на точкову опору
Такого типу проблема виникає в завданні опирання плити на одиночну колону при необхідності сприйняття крутних моментів відносно вертикальної осі колони. В цьому випадку можна рекомендувати введення абсолютно жорстких вставок (рис. 5.6).
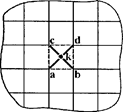
Рисунок 5.6 – Введення абсолютно жорстких вставок при обпиранні
плити на колону
Таке рішення з одного боку, вирішує проблему врахування «тіла» колони, тобто «зрізаються» піки моментів, що виникають при моделюванні опирання на колону як на точкову опору. З іншого боку, забезпечує сприйняття колоною крутних деформацій. У більшості ж випадків, коли є принаймні хоч би дві колони, цього не вимагається, оскільки крутний момент від деформацій в площині плити в цьому випадку сприйматиметься парами поперечних сил в колонах, а крутні моменти будуть малими і ними можна знехтувати.
Сполучення стержня рами з діафрагмою
Якщо до формування дискретної розрахункової схеми підходити чисто формально, описуючи пластину сукупністю скінченних елементів плоского напруженого стану, а стержневий каркас одновимірними елементами, і не робити жодних додаткових заходів, то в ригелях, що примикають до вузлів сполучення каркаса з діафрагмою, як згинні моменти, так і повздовжні і поперечні сили виходитимуть довільними.
Тут труднощі обумовлені тим, що скінченні елементи плоского напруженого стану (балки-стінки) не мають ступеня свободи відповідного куту повороту відносно осі, що перпендикулярна площині діафрагми. Оскільки програмний комплекс зажадає формального виконання всіх умов рівноваги, у тому числі і рівноваги кожного з вузлів по моментах, то ригелі, що жорстко примикають до вузлів діафрагми, зобов’язані будуть передати на вузли строго нульові моменти. В результаті згинні моменти в ригелях в цих вузлах виявляться рівними нулю, що відповідає розрахунковій схемі з шарнірним приєднанням ригелів до діафрагми.
Нехай, сталевий ригель певного перерізу заведений на частини своєї довжини в цегельну стіну, як це показано на рис. 5.7, а. Тоді в розрахунковій схемі, у тому числі і в дискретному її аналогу, досить врахувати проникаючий на відповідну довжину в область плоскої задачі одновимірний елемент-стержень.
Інший варіант розрахункової схеми можна запропонувати в разі монолітного сполучення залізобетонної стінної панелі і ригеля каркаса будівлі (рис. 5.7, б). Тут можна врахувати фактичні розміри перерізу – висоту ригеля, вздовж якої на межі діафрагми доречно розмістити абсолютно жорстке тіло.
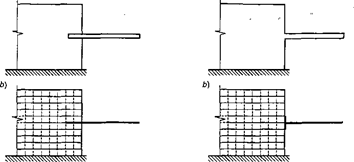
Рисунок 5.7 – Защемлення балки в стіні (а) та монолітне спряження ригеля з
діафрагмою (б)
Шрифти
Розмір шрифта
Колір тексту
Колір тла
Кернінг шрифтів
Видимість картинок
Інтервал між літерами
Висота рядка
Виділити посилання
Вирівнювання тексту
Ширина абзацу