Лекція 1.3 MATLAB у задачах прикладної математики
| Сайт: | Навчально-інформаційний портал НУБіП України |
| Курс: | Комп'ютерно-інтегровані технології. Ч1 ☑️ |
| Книга: | Лекція 1.3 MATLAB у задачах прикладної математики |
| Надруковано: | Гість-користувач |
| Дата: | понеділок, 2 березня 2026, 13:33 |
Опис
Розвиток науки змусив дослідників інтенсивно застосувати чисельні методи для рішення різних математичних задач. Чисельні методи створюються математиками і, як у системі MATLAB, пропонуються для застосування у вигляді готового інструменту. Програми, що реалізують певний чисельний метод, необхідно записувати в М-файл. Якщо не дати імені М-файлові, то він запишеться при виконанні програми в робочу папку під ім'ям Untitled (Безіменний). Такої ситуації варто уникати для виключення появи безлічі файлів з невизначеним ім'ям. Розглянемо рішення різних проблем обчислювальної математики, що мають важливе значення при вивчені різних наук.1. Табулювання функцій
Така задача широко використовується в екології, теплофізиці й інших дисциплінах. Звичайно функції, що описують який-небудь процес, досить громіздкі і створення таблиць їхніх значень вимагає великого обсягу обчислень.
Розглянемо два випадки табулювання функції:
1. З постійним кроком зміни аргументів.
2. З довільним набором значень аргументу.
Алгоритм реалізується шляхом організації циклу.
Приклад.
Обчислити 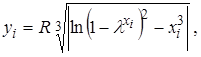
при: R = 4,28 × 10-2; λ = 2,87;
хi змінюється з кроком Δх = 2; хп = 2; хк = 10.
Введемо позначення λ →la = 2,87.
Протокол програми:
R = 4.28е-02; la = 2.87;
% Задається початкове значення х, крок dx і кінцеве значення х
х = 2.0 : 2.0 : 10.0;
![]()
% Для виведення значення y наприкінці рядка символ “;” не ставиться!
У вікні команд з'являються після натискання кнопки виконати значення функції y, що потім можна скопіювати в інший файл.
Результати обчислень:
ans =
|
2.0000 |
4.0000 |
6.0000 |
8.0000 |
10.0000 |
|
0.0682 |
0.1634 |
0.2517 |
0.3386 |
0.4250 |
Приклад.
Обчислити і вивести на екран значення функції
при х1 = 12,8; х2 = 23,4; х3 = 27,2; х4 = 17,8; х5 = 16,3; х6 = 14,9; а = 1,35; b = 0,98.
Таку задачу можна програмувати не змінюючи позначення змінних. Цикл організується для одномірного масиву.
Протокол програми:
а = 1.35; b = 0.98; х(1) = 12.8; х(2) = 23.4; х(3) = 27.2; х(4) = 17.8; х(5) = 16.3; х(6) = 14.9;
% Наприкінці рядка обчислення функції y символ “;” не ставиться.
|
у |
= |
|
|
|
|
0.3609 |
|
у |
= |
|
|
|
|
0.2327 |
|
у |
= |
|
|
|
|
0.1473 |
|
у |
= |
|
|
|
|
0.1800 |
|
у |
= |
|
|
|
|
0.1771 |
|
у |
= |
|
|
|
|
0.1658 |
Дані обчислень можна вивести у виді таблиці, якщо використовувати запис [x; y] без крапки з комою або [x y].
2. Розв’язок системи лінійних алгебраїчних рівнянь методом виключення Гаусса
До розв’язання систем лінійних рівнянь зводяться численні практичні задачі, наприклад різні крайові задачі для звичайних і в частинних похідних диференційних рівнянь. Можна стверджувати, що проблема є однієї з найпоширеніших і важливих задач прикладної математики.Нехай задана система п лінійних алгебраїчних рівнянь з n невідомими:
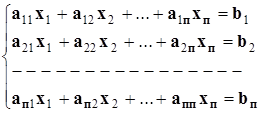 3.1
3.1
Система рівнянь (3.1) у матричній формі представляється в такий спосіб:
АХ = Y, (3.2)
де: А – квадратна матриця коефіцієнтів, розміром п ´ п рядків і стовпців;
Х – вектор-стовпець невідомих;
В – вектор-стовпець правих частин.
Систему рівнянь (3.2) можна вирішити різними методами. Один з найбільш простих і ефективних – метод виключення Гаусса і його модифікації. Його алгоритм базується на приведенні матриці А до трикутнокового вигляду (прямій хід) і послідовному обчисленні невідомих (зворотний хід). Ці процедури можна виконувати над невиродженими матрицями, у противному випадку метод Гаусса не застосовується.
Недоліком методу є нагромадження похибок у процесі округлення, тому метод Гаусса без вибору головних елементів використовується звичайно для рішення порівняно невеликих (п £ 100) систем рівнянь із щільно заповненою матрицею і не близьким до нуля визначником.
Якщо матриця А сильно розріджена, а її визначник не близький до нуля, то метод Гаусса придатний для рішення великих систем рівнянь. У MATLAB мається великий арсенал методів рішення систем рівнянь (3.2) методом виключення Гаусса. Для цього застосовуються наступні оператори:
|
/ |
- правий розподіл; |
|
|
|
|
\ |
- лівий розподіл; |
|
|
|
|
^ - 1 |
- зведення в степінь –1; |
|
|
|
|
inv(A) |
- звертання матриці А. |
Вирази
|
Х |
= |
Y/A |
|
Х |
= |
Y* А^ - 1 |
|
Х |
= |
Y* inv(A) |
|
Х |
= |
A\Y |
дають рішення ряду систем лінійних рівнянь АХ = Y, де А – матриця розміром m × n, Y – матриця розміром n × к.
Приклад.
Розв’язати систему 4-х лінійних рівнянь:
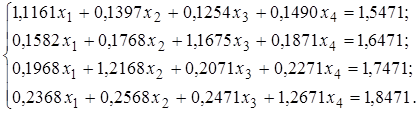
Протокол програми (у М-файлі)
|
а |
= |
[1.1161 0.1397 0.1254 0.1490 ; 0.1582 0.1768 1.1675 0.1871 ; 0.1968 1.2168 0.2071 0.2271 ; 0.2368 0.2568 0.2471 1.2671] ; |
|
b |
= |
[1.5471 ; 1.6471 ; 1.7471 ; 1.8471] ; |
<< Х4 = а \ b
Ця програма видає розв’язок заданої системи за допомогою четвертого оператора у виді матриці – стовпця:
|
Х4 |
= |
1.0406 0.9351 0.9870 0.8813 |
Увага. У М-файлі матриця а набирається по рядках, а елементи матриці правих частин b відокремлюються символом “;” , тобто теж набираються по рядках. Рішення іншими операторами системи рівнянь (3.2) вимагає набору матриці а по стовпцях, а елементи правих частин b відокремлюються тільки пробілом!
|
а |
= |
[1.1161 0.1582 0.1968 0.2368 ; 0.1397 0.1768 1.2168 0.2568 ; 0.1254 1.1675 0.2071 0.2471 ; 0.1490 0.1871 0.2271 1.2671] ; |
|
b |
= |
[1.5471 1.6471 1.7471 1.8471] ; |
<< Х1 = b/а
<< Х2 = b* a ^ - 1
<< Х3 = b* inv(a)
Результати розв‘язку:
|
Х1 |
= |
1.0406 0.9351 0.9870 0.8813 |
|
Х2 |
= |
1.0406 0.9351 0.9870 0.8813 |
|
Х3 |
= |
1.0406 0.9351 0.9870 0.8813 |
3. Апроксимація функцій
Одним із розповсюджених і практично важливих випадків зв'язку між аргументом і функцією є задання цього зв'язку у виді деякої таблиці {xi ; yi}, наприклад, експериментальні дані. На практиці часто доводиться використовувати табличні дані для наближеного обчислення y при будь-якому значенні аргументу х (з деякої області).
Цій меті служить задача про наближення (апроксимації) функцій: функцію f(x) потрібно приблизно замінити деякою функцією g(х) так, щоб відхилення g(х) від f(x) у заданій області було найменшим. Функція g(х) при цьому називається апроксимуючої. Якщо наближення будується на заданій дискретній множині {xi}, то апроксимація називається дискретною. До неї відносяться інтерполяція, середньоквадратичне наближення тощо.
При побудові наближення на безперервній множині (наприклад, на відрізку [a, b]) апроксимація називається безперервною або інтегральною.
MATLAB має засоби дискретної та безперервної апроксимації з візуалізацією результату.
Розглянемо дискретну апроксимацію (обробка експериментальних даних).
Приклад.
Використовуючи лінійну і поліноміальну апроксимації, одержати емпіричні формули для функції y=f(x), заданої в табличному виді:
|
xi |
0,75 |
1,50 |
2,25 |
3,00 |
3,75 |
|
yi |
2,50 |
1,20 |
1,12 |
2,25 |
4,28 |
Оцінити погрішність емпіричних формул.
Протокол програми. У вікні команд набираються значення xi і yi. Далі виконується команда побудови графіка тільки вузлових точок.
>> x = [0.75, 1.50, 2.25, 3.00, 3.75] ;
>> y = [2.50, 1.20, 1.12, 2.25, 4.28] ;
>> рlot (x, y, ¢ о ¢) ;
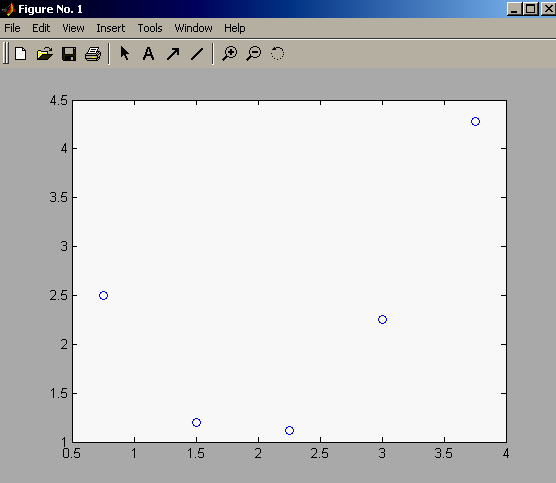 Рис. 3.1. Вузлові точки
Рис. 3.1. Вузлові точки
Увага. Варто пам'ятати, що при поліноміальній апроксимації максимальний степінь полінома на 1 менше числа експериментальних точок.
На панелі інструментів вікна графіка вузлових точок у меню Tools виконуємо команду Basic Fitting. З’являється вікно Основний Монтаж. У цьому вікні виділяються необхідні дані апроксимації. Зокрема, можна задати наступні операції:
- показати рівняння апроксимуючої функції y = g(х);
- вибрати метод підбору.
У нашій задачі вибираємо лінійну і поліноміальну апроксимації. У вікні графіка з’являються відповідні графіки і формули апроксимуючих функцій (рис. 3.2).
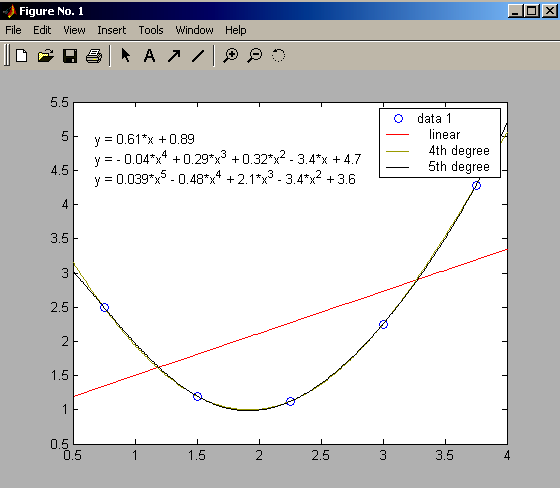
Рис. 3.2. Графіки і формули апроксимуючих функцій
Щоб встановити погрішність апроксимації, треба виділити параметр Графік залишку у вікні Основний Монтаж, і Показати норму залишків. Графік похибок з нормами можна винести в окреме вікно, або разом із графіком і апроксимуючими функціями – суб-графік.
Норма погрішностей вказує на статистичну оцінку средньоквадратичної похибки. Чим вона менше, тим точніше апроксимуюча функція y = g(х). У нашому прикладі:
Linear : norm of residuals (норма погрішності) = 2.1061
Quadratic : norm of residuals = 0.10736
Cubic : norm of residuals = 0.035857
4 th degree : norm of residuals = 9.6305e-015.
Графік погрішностей можна виводити у виді діаграм (зони), ліній (лінії) або окремих крапок (фрагменти). Сам графік погрішностей являє собою залежність різниці g(х) - f(x) в умовних точках, з'єднаних прямими лініями.
Крім лінійної і поліноміальної апроксимацій можна вибрати сплайн- апроксимацію – коли на кожнім інтервалі наближення використовується кубічний поліном з новими коефіцієнтами. У цьому випадку не можна одержати вираз для апроксимуючої функції, тобто така апроксимація є неповною.
4. Чисельний розв’язок звичайних диференціальних рівнянь
Багато задач фізики, хімії, екології, механіки й інших розділів науки і техніки при їхньому математичному моделюванні зводяться до диференційних рівнянь. Тому розв’язок диференціальних рівнянь є однієї з важливих математичних задач. У прикладній математиці вивчаються чисельні методи рішення диференційних рівнянь, що особливо ефективні з використанням комп’ютерно-інтегрованих технологій.
Серед чисельних методів розв’язків диференціальних рівнянь найбільш прості – це явні однокрокові методи. До них відносяться різні модифікації методу Рунге-Кутта.
Постановка задачі:
Потрібно знайти функцію y = f(х), що задовольняє рівнянню:
![]() (3.3)
(3.3)
і приймаючу при х = х0 задане значення y0:
![]() (3.4)
(3.4)
При цьому рішення необхідно одержати в інтервалі х0 £ х £ хк.. З теорії диференційних рівнянь відомо, що розв’язок y(х) задачі Коші (3.3), (3.4) існує, і є гладкою функцією, якщо права частина F(x, y) задовольняє деяким умовам гладкості.
Чисельне рішення задачі Коші методом Рунге-Кутта 4-го порядку полягає в наступному. На заданому інтервалі [х0, хк] вибираються вузлові точки. Значення розв’язку в нульовій точці відомо y(х0) = у0. У наступній точці y(х1) визначається за формулою:
![]() (3.5)
(3.5)
тут
 (3.6)
(3.6)
h – крок.
тобто, такий варіант методу Рунге-Кутта вимагає на кожнім кроці чотириразового обчислення правої частини рівняння (3.3). Цей алгоритм реалізовано у програмі ode45. Крім цієї програми MATLAB має у своєму розпорядженні великий набір аналогічних програм, що дозволяють успішно вирішувати звичайні диференційні рівняння.
Приклад.
Вирішити задачу Коші:
![]() , (3.7)
, (3.7)
Точний розв’язок має вигляд:
![]()
Розв’яжемо задачу за допомогою програми ode45. Спочатку в М-файл записуємо праву частину рівняння (3.7), сам М-файл оформляється як файл – функція, даємо йому ім'я F:
function dydx = F(x, y)
dydx = zeros(1,1);
dydx(1) = 2*(x^2+y(1));
Для чисельного рішення задачі Коші у вікні команд набираються відповідні оператори.
Протокол програми,
>>[X Y] = ode45 ( @ F , [0 1] , [1] ) ;
% Дескриптор @ забезпечує зв'язок з файлом – функцією правої частини
% [0 1] – інтервал на якому необхідно одержати розв’язок
% [1] – початкове значення розв’язоку
>> рlot (X,Y);
>> % Побудова графіка чисельного рішення задачі Коші (3.7)
>> hold on; gtext ( ¢ y(x) ¢)
% Команда дозволяє за допомогою мишки нанести на графік напис у(х)
>> [X Y]
>> % Остання команда виводить таблицю чисельного рішення задачі.
Результати рішення. Графік розв’язку задачі Коші (3.7) показаний на рисунку 3.3. Чисельне рішення представлене в таблиці 3.4, де наведено лише окремі вузлові точки. У програмі ode45 за замовчуванням інтервал розбивається на 40 точок із кроком h = 1/40 = 0,025.
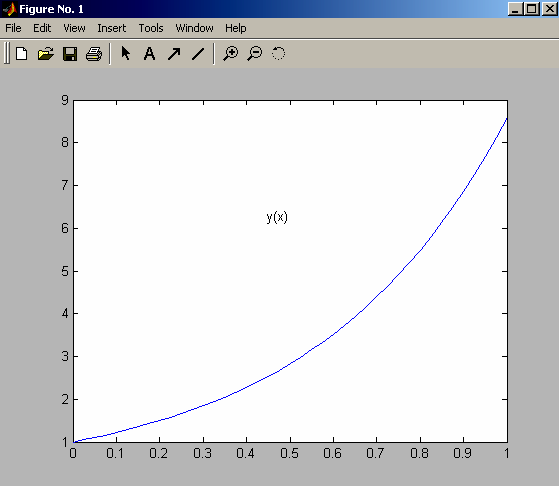
Рис. 3.3. Графік рішення задачі Коші
Таблиця 3.4
Табличне представлення чисельного рішення задачі Коші
|
хi |
Метод Рунге-Кутта |
Точне рішення |
|
0,0 |
1,0 |
1,0 |
|
0,1 |
1,2221 |
1,2221 |
|
0,2 |
1,4977 |
1,4977 |
|
0,3 |
1,8432 |
1,8432 |
|
0,4 |
2,2783 |
2,2783 |
|
0,5 |
2,8274 |
2,8274 |
|
0,6 |
3,5202 |
3,5202 |
|
0,7 |
4,3928 |
4,3928 |
|
0,8 |
5,4895 |
5,4895 |
|
0,9 |
6,8645 |
6,8645 |
|
1,0 |
8,5836 |
8,5836 |
Як продемонстровано у таблиці 3.4 чисельне рішення програмою ode45 є точним.
5. Наближене обчислення визначених інтегралів
До обчислень визначених інтегралів зводиться багато практичних задач фізики, хімії, екології, механіки й іншій природних наук. На практиці формулою Ньютона-Лейбніца не завжди вдається скористатися. У цьому випадку використовуються методи чисельного інтегрування. Вони базуються на наступних підходах: з геометричної точки зору визначений інтеграл являє собою площу криволінійної трапеції. Ідея методів чисельного інтегрування зводиться до розбивки інтервалу [a; b] на безліч менших інтервалів і перебуванню шуканої площі як сукупності елементарних площ, отриманих на кожному частковому проміжку розбивки. У залежності від використаної апроксимації виходять різні формули чисельного інтегрування, що мають різну точність. Розглянемо методи трапецій і Сімпсона (парабол).
Метод трапецій.
Тут використовується лінійна апроксимація, тобто графік функції y = f(x) представляється у вигляді ламаної, з'єднаної точками yi. Формула трапецій при постійному кроці ![]() , де n – число ділянок, має вигляд:
, де n – число ділянок, має вигляд:
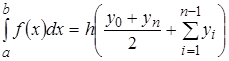 . (3.8)
. (3.8)
У MATLAB цю формулу реалізує програма trapz (x,y).
Метод Сімпсона
Якщо підінтегральну функцію замінити параболою, то формула Сімпсона з постійним кроком інтегрування:
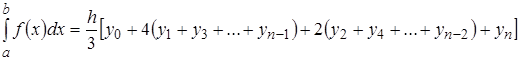 .(3.9)
.(3.9)
У MATLAB формула Сімпсона реалізується програмою quad, Підінтегральна функція може задаватися за допомогою дескриптора @, тоді вона програмується у файлі – функції, або за допомогою апострофів, тоді вона записується у самій програмі quad. Точність обчислення інтегралів за замовчуванням прийнята рівною 1×10-6.
Приклад.
Обчислити за методами трапецій і Сімпсона значення інтеграла
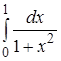
Протокол програми методу трапецій
>> x = 0 : 0.0001 : 1.0 ;
>> y = 1./ (1+x.^2) ;
>> z = trapz(x, y)
Результат обчислень
z =
0.7854
Протокол програми методу Сімпсона
>> quad ( ¢ (1./(1+x.^2)) ¢, 0, 1)
Результат обчислень
ans =
0.7854
Точне значення інтегралу дорівнює 0,785398163.
Як видно з прикладу отримані результати є практично точними, а самі протоколи досить прості.
6. Чисельне рішення нелінійних рівнянь
Задача знаходження коренів нелінійних рівнянь зустрічається в різних областях науково-технічних досліджень. Проблема формулюється в такий спосіб: нехай задана безперервна функція f(x) і потрібно знайти корінь рівняння
f(x) = 0.
Припустимо, що відомо інтервал зміни х [a; b], на якому необхідно досліджувати функцію f(x) і знайти значення х0, при якому f(x0) дорівнює або досить мало відрізняється від нуля.
Дана задача в системі MATLAB може бути вирішена в такий спосіб, Спочатку необхідно побудувати графік функції f(x) на заданому інтервалі і переконатися в існуванні кореня або декількох коренів. Потім застосувати програми пошуку коренів. Якщо існує один корінь і графік f(x) перетинає вісь х, то можна застосувати програму fzero. Якщо f(x) має більше одного кореня х, то варто застосувати більш функціональний оператор fsolve з пакету Optimization Toolbox, що вирішує задачу методом найменших квадратів. Програма fzero використовує відомі чисельні методи: розподіл відрізка навпіл, зворотної квадратичної інтерполяції.
Приклад.
Знайти корінь нелінійного рівняння 10х + 2х – 100 = 0 на інтервалі [1,0; 2,0].
Протокол програми
>> % Будуємо графік заданої функції
>> x = 1.0 : 0.001:2.0; y = 10.0.^x + 2.0*x – 100.0;
>> рlot (x, y) ; grid on
З'являється вікно з графіком функції 10х + 2х – 100 (рис. 3.4), з якого випливає, що корінь функції на заданому інтервалі існує. Для точного визначення кореня застосовуємо fzero і fsolve.
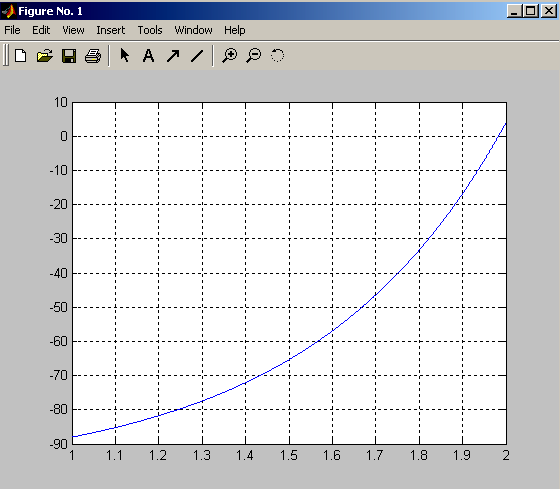
Рис. 3.4. Графік функції 10х + 2х – 100
>> Х1=fzero('(10.^x+2*x-100)',[1 2])
Результат розв’язку
Х1 =
1,9824
>> X2 = fsolve ( '(10.^x + 2.0*x - 100.0)', 1:2);
Результат рішення
Х2 =
1.9824
Шрифти
Розмір шрифта
Колір тексту
Колір тла
Кернінг шрифтів
Видимість картинок
Інтервал між літерами
Висота рядка
Виділити посилання
Вирівнювання тексту
Ширина абзацу