Чисельне рішення оптимізаційних задач
| Сайт: | Навчально-інформаційний портал НУБіП України |
| Курс: | Комп'ютерно-інтегровані технології. Ч1 ☑️ |
| Книга: | Чисельне рішення оптимізаційних задач |
| Надруковано: | Гість-користувач |
| Дата: | пʼятниця, 23 січня 2026, 04:43 |
Опис
Чисельне рішення оптимізаційних задач
та
Пакет оптимізації Optimization Toolbox
1. Чисельне рішення оптимізаційних задач
Під оптимізацією розуміють процес вибору найкращого варіанта з усіх можливих. З погляду інженерних розрахунків методи оптимізації дозволяють вибрати найкращий варіант конструкції, найкращий розподіл ресурсів, мінімальні збитки природному середовищу і т.п. У процесі розв’язку задачі оптимізації необхідно знайти оптимальні значення деяких параметрів, які називають проектними параметрами. Вибір оптимального рішення проводиться за допомогою деякої функції – цільової функції. Її можна записати у вигляді:
![]() , (4.1)
, (4.1)
де: х1, х2, … , хп – проектні параметри,
Можна виділити два типи задач оптимізації – безумовні й умовні. Безумовне завдання оптимізації полягає у пошуку максимуму або мінімуму функції 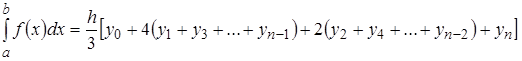 від n дійсних змінних і визначені відповідних значень аргументів на деякій множині G n-мірного простору. Звичайно розглядаються задачі мінімізації; до них легко зводяться і задачі на пошук максимуму шляхом заміни знака цільової функції на протилежний. Умовні задачі оптимізації – це такі, при формулюванні яких задаються деякі умови (обмеження) на множині G. Тут розглянемо тільки безумовні задачі оптимізації.
від n дійсних змінних і визначені відповідних значень аргументів на деякій множині G n-мірного простору. Звичайно розглядаються задачі мінімізації; до них легко зводяться і задачі на пошук максимуму шляхом заміни знака цільової функції на протилежний. Умовні задачі оптимізації – це такі, при формулюванні яких задаються деякі умови (обмеження) на множині G. Тут розглянемо тільки безумовні задачі оптимізації.
1.1. Пошук мінімуму функції однієї змінної
Для рішення цієї задачі використовуються методи золотого перетину або параболічної інтерполяції (у залежності від форми задання функції), реалізовані в програмі fminbnd.
Приклад.
Знайти мінімальне значення функції:
f(x) = 24 – 2x /3 + x2/30 на [5; 20].
Будуємо графік цієї функції, щоб переконатися в наявності мінімуму на заданому інтервалі.
Протокол програми
>> x = 5.0 : 0.001:20.0 ; y=24-2*x/3+x.^2/30;
>> рlot(x, y) ; grid on
З'являється вікно з графіком цієї функції (рис. 4.1), де відзначаємо наявність мінімуму.
Далі, для точного визначення координати і значення мінімуму використаємо функцію fminbnd:
>> [x, y] = fminbnd ( ¢ (24.0 – 2* x/3 + x,^2/30) ¢, 5.0, 20.0)
Результат пошуку
х =
10.0000
у =
20.6667
>> hold on; gtext ( ¢Minimum¢)
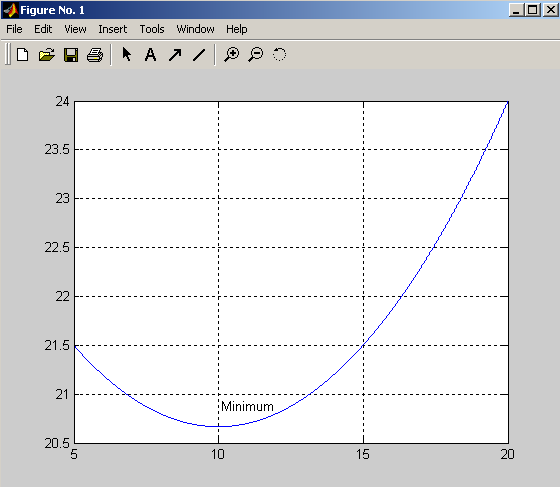
Рис. 4.1. Мінімальне значення функції f(x) = 24 – 2x /3 + x2/30
1.2. Пошук мінімуму функцій декількох змінних
Дана задача значно складніше попередньої. Розглянемо її рішення на прикладі функції двох змінних. Алгоритм можна використати для функцій більшого числа змінних. Для мінімізації функцій декількох змінних MATLAB застосовує симплекс – метод Нелдера-Міда. Такий метод є одним із кращих методів пошуку мінімуму функцій багатьох змінних, коли не обчислюються похідні або градієнт функції. Він зводиться до побудови симплекса в п-мірному просторі, заданого п + 1 вершиною. У двомірному просторі симплекс є трикутником, а в тривимірному – пірамідою. На кожному кроці ітерацій вибирається новий розв’язок всередині або поблизу симплексу. Він порівнюється з однієї з вершин симплекса. Найближча до нього вершина симплекса заміняється розв’язком. Таким чином, симплекс перебудовується і дозволяє знайти нове, більш точне положення розв’язку. Алгоритм пошуку повторюється, поки розміри симплексу за всіма змінними не стане менше заданої помилки.
Функцію, що реалізує симплекс-метод Нелдера-Міда, зручно використовувати в наступному записі:
[x, min f] = f min search ( … ),
де: х – вектор координат локального мінімуму;
minf – значення цільової функції в точці мінімуму.
Саму цільову функцію зручно представити за допомогою дескриптора @ у М-файлі.
Приклад.
Знайти координати і значення мінімуму функції двох змінних f(x, y) = (x2+ + y2 – 3)2 + (x2 + y2 – 2x – 3)2 + 1, якщо початкова точка пошуку має координати М0 (1; 1). Аналіз функції показує, що min f = 1 x = 0, .
Будуємо тривимірний графік цієї функції, щоб переконатися в наявності мінімуму. Візьмемо інтервал х є [-1; 1]; y є [1; 3].
Протокол програми
>> [x,y] = meshgrid ( [-1 : 1, 1 : 3] ) ;
>> z=(x.^2+y.^2-3).^2+(x.^2+y.^2-2*x-3).^2+1;
>> рlot 3 (x,y,z) (рис. 4.2)
Рис. 4.2. Поверхня функції f(x, y) = (x2+ + y2 – 3)2 + (x2 + y2 – 2x – 3)2 + 1
Після побудови тривимірного графіка виконуємо пошук мінімуму, у М-файлі програмуємо цільову функцію:
function f = Fxy(x)
f = ((x(1)^2+x(2)^2-3)^2-3)^2+((x(1)^2+x(2)^2-2*x(1)-3)^2)+1;
Вирішуємо поставлену задачу у вікні команд:
>> [xmin, minf] = fminsearch ( @Fxy, [1; 1] )
Результати пошуку
xmin =
- 0.0000 1.7320
minf =
1.0000
Як видно, результати рішення задачі точні.
2. Пакет оптимізації Optimization Toolbox
Пакет оптимізації (Optimization Toolbox) – це бібліотека функцій, що розширюють можливості системи MATLAB за чисельними обчисленнями і призначена для рішення задач оптимізації і систем нелінійних рівнянь. Підтримує основні методи оптимізації функцій ряду змінних:
- безумовна оптимізація нелінійних функцій;
- метод найменших квадратів;
- розв’язок нелінійних рівнянь;
- лінійне програмування;
- квадратичне програмування;
- умовна мінімізація нелінійних функцій;
- методи мінімакса;
- багатокритеріальна оптимізація.
Розглянутий пакет дає можливості вирішувати задачі мінімізації функцій, перебору розв’язку рівнянь, задачі апроксимації («припасування» кривих під експериментальні дані).
Різні типи таких задач разом із застосовуваними для їхнього рішення функціями пакету (Optimization Toolbox) приведені в таблиці 5.1.
Таблиця 5.1.
Типи задач, розв'язуваних засобами пакета Optimization Toolbox
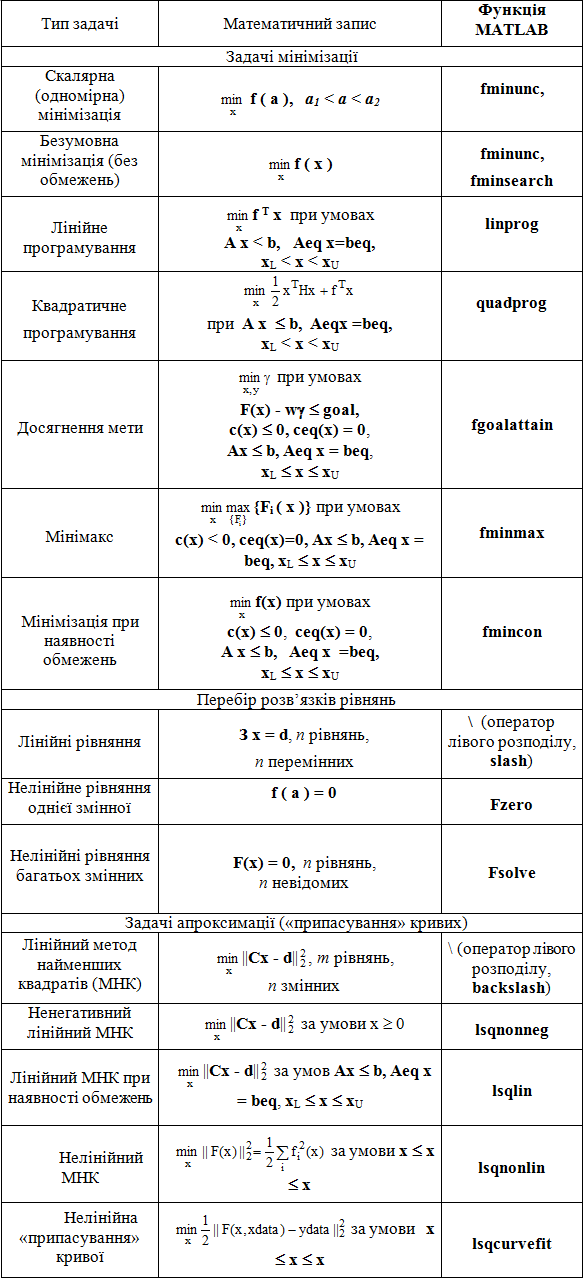
Прийняті позначення: а – скалярний аргумент; х, у – у загальному випадку векторні аргументи; f(а), f(х) – скалярні функції; F(x), c(x), ceq(x), K(x, w) – векторні функції; •А, Aeq, З, Н – матриці; b, beq, d, f, w, goal, xdata, ydata – вектори.
У рамках пакета Optimization Toolbox усі задачі оптимізації поділяються на дві групи: задачі малої і середньої розмірності і задачі великої розмірності. Відповідно, такий же розподіл прийнятий для алгоритмів рішення таких задач. Зрозуміло, це не означає, що для розв’язку задач середньої розмірності не можна застосовувати алгоритми великої розмірності і навпаки. Просто алгоритми тієї або іншої групи більш ефективні для задач своєї розмірності.
У пакеті (Optimization Toolbox) реалізовано широкий набір алгоритмів для рішення задач оптимізації середньої і малої розмірності. Основними для задач без обмежень є симплексний метод Нелдера-Міда і квазіньютоівскі методи. Для рішення задач з обмеженнями, мінімакса, досягнення мети і використані алгоритми квадратичного програмування.
Задачі, що зводяться до нелінійних МНК, вирішуються за допомогою алгоритмів Ньютона-Рафсона і Левенберга-Марквардта.
Допоміжні процедури одномірної (скалярної) оптимізації використовують алгоритми квадратичної (параболічної) і кубічної інтерполяції.
Розглянемо найбільше часто застосовувані в задачах оптимізації функції лінійного (linprog) і нелінійного (fmincon) програмування.
2.1. Функція fmincon
furincon — функція пошуку мінімуму скалярної функції багатьох змінних при наявності обмежень виду:
с(х) ≤0, ceq(x) = 0 ,
А х ≤ b, Aeq x = beq,
lb < х < ub
Функція записується у виглядах:
х = fmincon( fun, x0, A, b),
х = fmincon( fun, x0, A, b, Aeq, beq),
х = fmincon( fun, x0, А, b, Aeq, beq, lb, ub),
х = fmincon( fun, x0, A, b, Aeq, beq, lb, ub, nonlcon),
х = fmincon( fun, x0, A, b, Aeq, beq, lb, ub, nonlcon, options),
х = fmincon( fun, x0, A, b, Aeq, beq, lb, ub, nonlcon, opt1ons, Pl, P2, ...).
[x, fval] = fmincon(...) – повертається не тільки оптимальне значення векторного аргументу, але і значення цільової функції в точці мінімуму fval;
[x, fval, exitflag] = fmincon(…) – те ж, що і попередня функція, але повертається ще інформація про характер завершення обчислення exitflag;
[x, fval, exitflag, output] = fmincon(…) – те ж, що і попередня функція, але додатково повертається інформація про результати оптимізації (вихідна структура) output;
[x, fval, exitflag, output, lambda] = fmincon(...) – те ж, що і попередня функція, але повертаються ще множники Лагранжа lambda;
[x, fval, exitflag, output, lambda, grad] = fmincon(…) – те ж, що і попередня функція, але повертається ще й величина градієнта функції в точці мінімуму grad;
[x, fval, exitflag, output, lambda, grad, hessian] = fmincon(…) – те ж, що і попередня функція, але повертається ще й величина гессіана H функції в точці мінімуму.
Приклад.
Нехай потрібно знайти мінімум функції f(х) = - x1×x2×x3, при початковому значенні х = [10; 10; 10] і наявності обмежень:
0 ≤ x1 + 2 x2 + 2 x3 ≤ 72.
Розв’язок. Спочатку створимо М-файл, що визначає цільову функцію:
function f = myfun(x)
f =- x(1)*x(2)*x(3) ;
Потім запишемо обмеження у виді нерівностей:
- x1 - 2 x2 - 2 x3 ≤ 0
x1 + 2 x2+ 2 x3 ≤ 72,
або в матричній формі:
А ≤ b,
де: ![]() .
.
Тепер розв’язок представляється у такий спосіб:
» А = [-1 -2 -2; 1 2 2];
» b = [0; 72];
» x0 = [10; 10; 10]; % Початкові значення
» [x, fval] = fmincon('myfun', x0, A, b)
x =
24.0000
12.0000
12.0000
fval =
-3.4560e+003
2.2. Функція linprog
Функція linprog забезпечує рішення задачі лінійного програмування.
Функція записується у виді:
х = linprog(f,A,b,Aeq,beq),
х = linprog(f,A,b,Aeq,beq,lb,ub),
х = linprog(f,A,b,Aeq,beq,lb,ub,x0),
х = linprog(f,A,b,Aeq,beq,lb,ub,x0,options),
[x,fval] = linprog(...),
[x,fval,exitflag] = linprog(...),
[x,fval,exitflag,output] = linprog(...),
[x,fval,exitflag,output,lambda] = linprog(...).
Приклад.
Цех малого підприємства повинен виготовити 100 виробів трьох типів. Кожного виробу потрібно зробити не менш 20 штук. На вироби іде відповідно 4, 3,4 і
Скільки виробів кожного типу х1 , х2 і х3 треба випустити для одержання максимального випуску в грошовому вираженні, якщо ціна виробу складає по калькуляції 40, 30 і 20 грн?
Задача зводиться до обчислення максимуму функції
f(x1,x2,x3) = 40 x1 + 30 x2 + 20 x3
при наявності обмежень
x1 ≥ 20, x2 ≥ 20, x3 ≥ 20
4 x1 + 3,4 x2 + 2 x3 ≤ 340
4,75 x1 + 11 x2 + 2 x3 ≤ 700
x1 + x2 + x3 = 100
Маємо задачу лінійного програмування.
f=[40;30;20];% вектор коефіцієнтів лінійної цільової функції
% Матриця коефіцієнтів обмежень – нерівностей
A=[4 3.4 2; 4.75 11 2];
b=[340;700]; % вектор обмежень – нерівностей
Aeq=[1 1 1]; % матриця коефіцієнтів обмежень – рівностей
beq=[100]; % вектор обмежень – рівностей
% Задання нижніх границь змінних (нулів)
lb=[20;20;20];
% Пошук рішень, визначення максимум цільової функції
[x, fval, exitflag, output]=linprog(-f, A, b, Aeq, beq, lb)
Optimization terminated successfully
x =
56.0000
20.0000
24.0000
fval =
-3.3200e+003
exitflag =
1
output =
iterations: 5
cgiterations: 0
algorithm: 'lipsol'
Шрифти
Розмір шрифта
Колір тексту
Колір тла
Кернінг шрифтів
Видимість картинок
Інтервал між літерами
Висота рядка
Виділити посилання
Вирівнювання тексту
Ширина абзацу