Тема 5. Моделі просторових даних в ГІС
| Сайт: | Навчально-інформаційний портал НУБіП України |
| Курс: | Візуалізація геопросторових даних ☑️ |
| Книга: | Тема 5. Моделі просторових даних в ГІС |
| Надруковано: | Гість-користувач |
| Дата: | субота, 7 березня 2026, 21:57 |
Зміст
- 1. Тема 5. Моделі просторових даних в ГІС
- 2. Моделі даних. Карта як модель місцевості та носій інформації про навколишній світ
- 3. Растровий спосіб
- 4. Векторний спосіб
- 5. Порівняння векторних і растрових моделей
- 6. Атрибутивна інформація (атрибутивні моделі даних)
- 7. Процес проектування атрибутивної БД
- 8. Презентація та додаткові відеоматеріали
1. Тема 5. Моделі просторових даних в ГІС
ПЛАН
- Моделі даних. Карта як модель місцевості та носій інформації про навколишній світ.
- Векторне представлення просторових даних.
- Растрове представлення просторових даних.
- Порівняння векторних і растрових моделей.
- Атрибутивна модель даних.
- Процес проектування атрибутивної БД
-
Презентація та додаткові відеоматеріали
2. Моделі даних. Карта як модель місцевості та носій інформації про навколишній світ
Всесвіт навколо нас наповнений реальними об’єктами, явищами і системами, а все, що ми про них знаємо і відображаємо будь-якими способами, є їхніми моделями. Отримані знання про модель є придатними для екстраполяції їх на аналогічні об’єкти в природі.
Модель є штучною (часто віртуальною) системою, яка служить засобом здобуття інформації про реальну (штучну чи природну) систему різними методами дослідження. Тобто, модель – це створена аналітиком система, яка відтворює взяті для вивчення, вагомі для поставленої мети пізнання, сторони (елементи, властивості, відношення, параметри) об’єкта (явища) і служить опосередкованим засобом здобуття знання про цей об’єкт. Відповідно, моделювання є відтворенням певних ознак і властивостей системи-оригінала на створеному за вибраними методами аналізі.
Будь-які Моделювання – це завжди порівняння відомого (достовірного) з новим (невідомим) за аналогіями. Спираючись на аналогії, дослідник висуває гіпотези – передбачення, здогадки, які згодом перевіряє шляхом експериментів.
Отже, модель – це уявна чи матеріально реалізована система, яка відображаючи чи відтворюючи об’єкт, здатна змінювати його так, що її вивчення дає нам нову інформацію про ці об’єкти.
Реальні об’єкти й явища спочатку фіксують термінами (словесні описи), відображають малюнками, світлинами, графіками, діаграмами, математичними формулами.
Об’єктивно існують дві основні групи моделей: матеріальні (тобто фізичні або дієві) і абстрактні (ідеальні, уявні). За своєю природою матеріальні моделі бувають предметні та знакові. Предметні моделі поділяють на природні (натурні) й виготовлені (фізичні) макети, а знакові – на мовні (вербальні) й математичні (статистичні, імітаційні тощо).
За складом підтримуючих моделей даних можна робити висновки про потенційні можливості й характер функцій просторового аналізу в ГІС.
Моделлю подання даних називається система концепцій і правил, яка використовується для опису типів об’єктів та взаємозв’язків між ними та їх елементами.
Модель просторової інформації визначає характер практично всіх наступних операцій і методів аналізу інформації, спосіб вводу даних і особливості отримуваних результатів.
Перехід між різними моделями даних хоч і можливий, але складний, потребує значних додаткових затрат праці і може призвести до безповоротних втрат інформації.
Найбільш поширеними моделями представлення даних в ГІС є векторна (топологічна і нетопологічна) і растрова моделі.
Вибір тієї чи іншої моделі в ГІС є питанням значно принциповішим і визначальнішим, ніж вибір конкретного програмного забезпечення.
Цифрова топографічна карта (план) - це цифрова модель місцевості, сформована з урахуванням законів картографічної генералізації у деякій картографічній проекції, системі координат і висот, у прийнятій системі умовних позначень, із врахуванням топологічних взаємозв’язків між об’єктами, створена за допомогою спеціальних програмних засобів на ПК.
Цифрові топографічні карти одержують шляхом запису просторових координат об'єктів місцевості і кодів їх характеристик в числовому вигляді в процесі польового топографічного знімання, а також картометричним (за графічними оригіналами) або фотограмметричним шляхом (за аерокосмічними знімками).
Відомо, що карта є графічним представленням географічних даних. Для того, щоб служити ефективним джерелом інформації, карта повинна бути максимально візуально зрозумілою. Принцип графічного дизайну – розміри, пропорції, розміщення, баланс, символи, типографія – є необхідними для карти так само, як для будь-якого іншого типу ілюстрацій. Читаючи карту, можна отримати інформацію про форму, та розташування географічних об’єктів, про певні атрибутивні дані, пов’язані з цими об’єктами, про певні просторові взаємозв’язки між об’єктами.
ГІС дає можливість отримати специфічну інформацію з карт, наприклад, поширення, щільність, взаємозв’язки та тенденцію певних об’єктів, інтегрування та накладання різних картографічних даних, пошук оптимальних шляхів та напрямів руху, моделювання і прогнозування процесів у майбутньому.
Карта в ГІС перетворюється зі статистичного об’єкта в динамічну модель і презентацію просторових даних.
Типи і способи представлення даних в гіс (Моделі даних)
Просторова інформація в ГІС складається з метричної частини, яка описує позиційні властивості об’єктів, та з пов’язаної з нею змістової (семантична, тематична) частини, іншими словами атрибути (англ.). Відповідно, просторові дані в ГІС поділяються на позиційні та атрибутивні.
Позиційні дані описують просторові характеристики різних об'єктів, таких як дороги, будівлі, водойми, лісові масиви. Реальні об'єкти можна розділити на дві абстрактні категорії: дискретні (будинки, територіальні зони) і безперервні (рельєф, рівень опадів, середньорічна температура).
Існує два способи представлення позиційної інформації — векторний та растровий.
3. Растровий спосіб
Растрові дані зберігаються у вигляді наборів величин, упорядкованих у формі прямокутної сітки. Растрові моделі становлять мережу двомірного масиву точок, або растр, комірки якої називаються пікселями (picture x element). Найпоширенішим способом отримання растрових даних про поверхню Землі є дистанційне зондування та сканування. Найчастіше растр використовують для безперервних об'єктів. Відмінність між растровою моделлю і зображенням полягає в тому, що комірка першого зберігає код явища, а другого – величину яскравості.
Зберігання растрових даних може здійснюватися в графічних форматах:
APNG — Animated PNG, BMP, ECW, DRG — digital raster graphic, GIF, ICO (Windows Icon), ILBM, JPEG, JPEG 2000, JPEG XR, MNG,PBM, PGM, PPM, PNM, PCX, PNG, PSD, TGA, TIFF, WMP, XPM або в бінарному вигляді в базах даних.
4. Векторний спосіб
Просторова інформація у векторних форматах зберігається у вигляді x, y координат у прямокутній системі координат. Місцезнаходження кожного об’єкта на карті описується рівнянням
F = f (x, y, z, n1, n2….),
де x, y –координати точок, які визначають положення об’єкта;
z – висота об’єкта над рівнем моря;
n1, n2 … - атрибутивні дані об’єкта.
У наш час відомо багато різних векторних форматів подання даних (моделей даних), які призначені для зберігання цифрової картографічної інформації. Усі вони відрізняються один від одного складністю обраних моделей подання даних, і відповідно, можливостями їх використання, маніпулювання й аналізу. У найпростіших міститься інформація тільки про геометричні зв’язки об’єктів, у більш складних додається інформація про топологічні сутності об’єктів і їхні атрибути.
Дискретні об'єкти та безперервні поля величин представляють за допомогою сукупності геометричних фігур — векторних об'єктів. Найпоширенішими типами векторних об'єктів є:
· Точки — Використовуються для позначення географічних об'єктів, для яких важливо розташування, а не їхня форма або розміри. Можливість позначення об'єкта точкою залежить від масштабу карти. У той час як на карті світу міста доцільно позначати точковими об'єктами, то на мапі міста саме місто представляється у вигляді безлічі об'єктів. У ГІС точковий об'єкт зображується у вигляді деякої геометричної фігури невеликих розмірів (квадратик, гурток, хрестик), або піктограмою, що передає тип реального об'єкта.
· Полілінії — Призначені для зображення лінійних об'єктів. Полілінія — ламана лінія, складена з відрізків прямих. Полілінією зображуються дороги, залізничні колії, річки, вулиці, водопровід. Допустимість зображення об'єктів полілінією також залежить від масштабу карти. Наприклад, велика річка в масштабах континенту цілком може зображуватися лінійним об'єктом, тоді як вже в масштабах міста потрібно її зображати просторовим об'єктом. Характеристикою лінійного об'єкта є довжина.
· Багатокутники (многокутники чи полігони) — Призначені для позначення просторових об'єктів з чіткими кордонами. Прикладами можуть виступати озера, парки, будівлі, країни, континенти. Характеризуються площею і довжиною периметра.
Векторні дані добре підходять для передачі інформації про дискретні географічні об'єкти, але можуть описувати також безперервні поля величин. Поля при цьому зображуються у вигляді ізоліній або контурних ліній. Одним із способів подання рельєфу є нерегулярна тріангуляційна сітка. Така сітка формується безліччю точок з прив'язаними значеннями (в даному випадку висота). Значення в довільній точці всередині сітки виходять шляхом інтерполяції значень у вузлах трикутника, в який потрапляє ця точка.
При побудові ГІС застосовують набір базових геометричних даних, з яких потім компонують інші більш складні дані. У ГІС використовуються такі типи атомарних геометричних даних:
· точка (вузол, вершина);
· лінія незамкнута;
· контур (лінія замкнута);
· полігон (ареал, район) - група прилеглих один до одного замкнутих ділянок;
· просторова мережа (розвиток типу «полігон»).
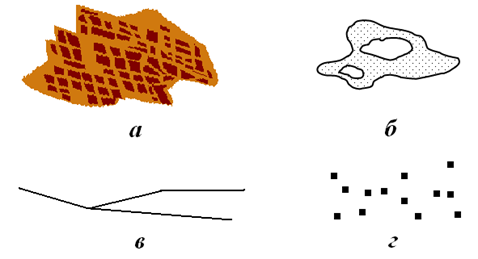
Складні типи даних у ГІС: а) міські квартали у вигляді полігональних об’єктів;
б – полігональний об’єкт із регіонами виключення; в – полілінія; г – мультиточковий об’єкт
На практиці з цих атомарних моделей формуються складні складові моделі. У різних ГІС вони відрізняються, тому як приклад будемо надалі розглядати моделі ГІС Географ (GeoGraph). Основні елементи промислового пакета Географ наступні (рис. 2.14):
1. Точка - геометричний об'єкт, заданий парою координат Х і У.
2. Відрізок - лінія, що з'єднує дві точки.
3. Вершина (вертекс) - початкова або кінцева точка відрізка.
4. Дуга (полілінія) - впорядкований набір зв'язкових відрізків.
5. Вузол - початкова або кінцева вершина дуги.
6. Символ із вузол - вузол, що належить тільки однієї дузі, у якої початкова та кінцева вершини не збігаються.
7. Псевдовузол - вузол, що належить двом дуг або однієї замкнутої дузі, у якої початкова та кінцева вершини збігаються (вузол, при проходженні якого немає альтернативи вибору подальшого шляху).
8. Нормальний вузол - вузол, що належить трьом або більше дуг, або вузол, що належить двом дуг, одна з яких самозамкнутості на цьому вузлі, а друга примикає до нього (вузол, при проходженні якого є можливість вибору подальшого шляху).
9. Замкнута дуга - дуга, у якої збігаються початкова та кінцева вершини (дуга, у якої є тільки один вузол).
10. Полігон - область, обмежена замкнутою дугою або впорядкованим набором пов'язаних дуг, які утворюють замкнутий контур.
11. Покриття - набір файлів, які фіксують у вигляді цифрових записів просторові об'єкти і структуру відносин між ними.
12. Порожнє покриття - покриття, на якому відсутні просторові об'єкти.
13. Шар - покриття, що розглядається в контексті його змістовної визначеності (рельєф, рослинність та ін.)
14. Внутрішній ідентифікатор просторового об'єкта - ціле число, що є службовим ідентифікатором об'єкта (унікальне ім'я для кожного об'єкта даного покриття, яка призначається автоматично в процесі роботи редактора).
15. Користувальницький ідентифікатор просторового об'єкта - ціле число, що служить для зв'язку об'єктів цифрової карти з таблицями тематичних даних.
5. Порівняння векторних і растрових моделей
Векторні дані зазвичай мають набагато менший розмір, ніж растрові. Їх легко трансформувати і проводити над ними бінарні операції. Векторні дані легко перетворити на растрові в той час як обернена операція набагато складніша. Векторні дані дозволяють проводити різні типи просторового аналізу, наприклад пошук найкоротшого шляху в дорожній мережі. Проте з растром простіше проводити оверлейний аналіз.
6. Атрибутивна інформація (атрибутивні моделі даних)
У ГІС до векторних об'єктів можуть бути прив'язані семантичні дані. Наприклад, на карті територіального зонування до просторових об'єктів, які становлять зони, може бути прив'язана характеристика типу зони. Структуру і типи даних визначає користувач. На основі атрибутивних значень, присвоєних векторним об'єктам на карті, може будуватися тематична карта, на якій ці значення позначені кольорами відповідно до шкали кольорів або різного роду штрихуванням чи точками. Найчастіше атрибутивні дані зберігаються у таблицях реляційної бази даних та є прив'язаними до певних векторних об'єктів. У випадку використання растрового способу позиційна та атрибутивна інформація поєднуються — колір піксела передає одночасно і розташування і характеристику.
Розглянемо особливості, властиві основним елементам векторних даних ГІС.
Точкові об'єкти. До найпростіших типам точкових об'єктів відносяться не тільки власне точки, але й умовні точкові знаки. Наприклад, знаком «Нафтова вишка» може бути позначено родовище. Це точковий об'єкт. Вибір об'єктів, що позначаються точками, залежить від масштабу карти. На великомасштабних картах точками позначаються окремі будови, а на дрібномасштабних - міста і навіть країни. Особливістю точкових об'єктів є те, що вони зберігаються як у вигляді графічних файлів, так і у вигляді таблиць, як атрибути, тому що координати точок розглядаються як дві додаткові характеристики. Таким чином, інформацію про набір точок можна представити у вигляді розгорнутої таблиці, в якій окрім координат можуть знаходитися і інші атрибути кожній з точок-об'єктів. У таких таблицях кожному рядку відповідає об'єкт-точка, кожному колонку - ознака, відповідний типізовану даному (або координата, або атрибут).
Лінійні об'єкти. Вони використовуються для опису мереж (наприклад, дорожня, транспортна, телефонна, гідрологічна мережа). Будь-яка мережа складається з вузлів (вершин) та відокремлених ліній і дуг (Ланок). Для кожного вузла у лінійних об'єктів існує характеристика - валентність.
Валентність вузла - це кількість суміжних вузлу дуг. Кінці відокремлених ліній одновалентних. Для вуличних мереж (перетин вулиць) валентність найчастіше дорівнює чотирьом. У гідрографії частіше зустрічаються тривалентні вузли (основне русло річки і приплив).
Лінійні об'єкти, як і точкові, мають свої атрибути, причому різні для дуг і для належних їм вузлів. Приклади атрибутів, застосовуваних для опису дуг:
· дорога: атрибути - напрямок руху, інтенсивність руху, протяжність;
· транспортна магістраль: кількість смуг для руху; час у дорозі;
· газопровід: діаметр труби, напрямок руху газу;
· лінія ЛЕП: напруга ЛЕП.
· перехрестя: наявність підземного переходу, назви перетинають вулиць;
· підстанція ЛЕП: характеристика трансформатора ЛЕП;
· пішохідний перехід: наявність світлофора, ширина переходу, наявність острівця безпеки та ін
Деякі атрибути можуть служити для зв'язку з іншими об'єктами (наприклад, назви перетинають вулиць). Часто для включення додаткових атрибутів потрібно розбивати лінійні об'єкти і створювати нові вузли: наприклад, частина русла річки забруднена, її розбивають на чисту частину річки та забруднену і описують їх по-різному.
Ареали або полігони. В одній ГІС може бути представлено кілька типів ареалів: наприклад, економічні зони, дані про сільськогосподарські угіддя та ін. Часто межі ареалів визначити по карті або фотознімку можна - їх встановлюють штучно, наприклад, зони на території міста, забруднені викидами підприємств, економічні зони та ін.
7. Процес проектування атрибутивної БД
Просторові об’єкти шарів і їх моделі
При цифруванні карт виділяється три типи об'єктів, до яких можна віднести будь-який з наявних на карті:
А) Точковий об'єкт
Б) Лінійний об'єкт
В) Полігональний об'єкт
Точковий об’єкт
Об'єкт, позначений точкою, оскільки його розміри занадто малі, щоб можна було відобразити його форму (межі, площу) в масштабі карти. Може також представляти якийсь умовний об'єкт, який не має розмірів, наприклад, позначку висот.
Лінійний об’єкт
Об'єкт, локалізований у вигляді лінії, оскільки його ширина не виражається в масштабі карти-джерела - річка, дорога і т.д. Може також представляти якийсь умовний об'єкт, наприклад, кордон.
Полігональний об’єкт
Об'єкт, що має площу, яка виражається в масштабі карти-джерела. Визначається замкнутим контуром і його внутрішньою областю, наприклад, ліс, озеро.
Можливості ГІС
Можливості ГІС значною мірою залежать від того, якими моделями вона підтримує примітиви просторових шарів. Складність моделі повинна відповідати складності реальних об'єктів і складності розв'язуваних завдань. У ГІС, допускають тривимірне моделювання, таких як наприклад AutoCAD Map і AutoCAD Civil, крім класичних об'єктів, можуть також використовуватися 3D-поверхні і 3D-solid моделі.
Векторні моделі
Більша частина функцій і задач моделювання просторових об'єктів ГІС може бути реалізована на основі векторних моделей (у вигляді точок, ліній і полігонів). Векторні моделі особливо зручні для подання та зберігання дискретних об'єктів, таких як будівлі, трубопроводи або межі ділянок.
Точки, лінії та полігони
Точки - це пари координат (х, у) або трійки координат (х, у, z, де z - висота).
Лінії - набори координат, що визначають конкретну форму.
Полігони - набори координат, що визначають межі замкнутих областей.
Значення координат залежать від географічної системи координат, в якій зберігаються дані.
Векторні дані
ГІС можуть зберігати векторні дані в класах просторових об'єктів і наборах топологічно-пов'язаних класів об'єктів. У другому випадку ми маємо справу вже з векторною топологічною моделлю. Атрибути, пов'язані з об'єктами, зберігаються в таблицях даних.
Векторні топологічні моделі
У топологічному шарі в процесі його створення і редагування створюються і фіксуються як самі просторові об'єкти, так і просторові відносини між зазначеними об'єктами - зв'язність, сусідство, суміжність, вкладеність і контролюють цілісність об'єкту. При цьому об'єкти типу «Полігон» створюються в результаті збирання полігонів з дуг, що утворюють замкнуті контури. Завдяки своїм властивостям топологічні моделі забезпечують вирішення просторових задач. У ГІС застосовуються вузлові топології (Node Topology), мережеві топології (Network Topology) і полігональні топології (Poligon Topology).
Вузли
Залежно від того, скільки дуг об'єднано в одному вузлі, вузли можуть позначатися по-різному і відрізнятися як:
Δ - нормальні вузли (три і більше дуг);
◊ - псевдовузли (дві дуги, в тому числі різні кінці однієї дуги);
· - Висячі вузли (одна дуга).
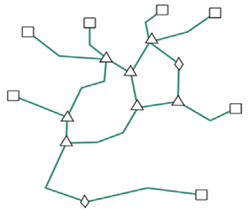
Полігон
Елементом полігональної топології є полігон. При створенні полігональної топології створюються і мережева, і вузлова топології. На рисунку показано приклад сусідства двох полігонів. Кожен полігон може характеризуватися наступним набором даних:
(ID, Area, N, X, Y), де ID - ідентифікатор полігону; Area - його площа; N - кількість ребер, обмежуючих полігон; X, Y - координати центроїда полігону.
Центроїд
Центроїд - це точка, що обов'язково лежить всередині полігону. Існують різні алгоритми її автоматичного вибору. Однак, після автоматичного вибору Центроїд може бути вручну перенесений в іншу внутрішню точку. При автоматичному створенні топології, Центроїди можуть бути також призначені попередньо з числа (з шару) точкових об'єктів (Наприклад, обласний центр може бути призначений як Центроїд області на карті Росії).
Моделі даних
ГІС є цифровою моделлю світу. Вибір моделі визначає, як реальний світ моделюється на комп'ютер і наскільки він корисний для іншого аналізу
Існують такі моделі даних:
А) Спагетті модель
Б) Топологічні моделі(GBF/DiIME, TIGER, POLYVRT)
В) Географічні моделі даних
Г) Моделі даних ESRI
Д) Растрові моделі даних (та операції над растрами)
Е) Гріди
Є) Моделі TIN
Ж) Об'єктно-орієнтована модель
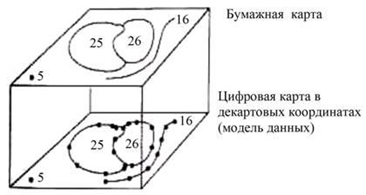
Спагетті модель
Найпростішої векторної структурою даних є спагетті-модель, наведена на малюнку, яка по суті переводить "один в один" графічне зображення карти. Можливо, вона представляється як найбільш природна або найбільш логічна, в основному тому, що карта реалізується як умоглядна модель. Хоча назва звучить трохи дивно, воно насправді дуже точно по суті. Якщо уявити собі покриття кожного графічного об'єкта нашої паперової карти шматочком (одним або кількома) макаронів, то ви отримаєте досить точне зображення того, як ця модель працює. Кожен шматочок діє як один примітив: Дуже короткі - для точок, більш довгі - для відрізків прямих, набори відрізків, з'єднаних кінцями, - для кордонів областей. Кожен примітив - одна логічна запис в комп'ютері, записана як рядки змінної довжини пар координат (X, Y).
Топологічні моделі
На відміну від спагетті-моделі, топологічні моделі, як це випливає з назви, містять топологічну інформацію в явному вигляді. Для підтримки просунутих аналітичних методів потрібно внести в комп'ютер як можна більше явної топологічної інформації. Подібно до того, як математичний співпроцесор об'єднує багато спеціалізованих математичних операцій, так і топологічна модель даних об'єднує вирішення деяких з найбільш часто використовуваних в географічному аналізі функцій. Це забезпечується включенням до структури даних інформації про суміжності для усунення необхідності визначення її при виконанні багатьох операцій. Топологічна інформація описується набором вузлів і дуг. Вузол - більше, ніж просто точка, зазвичай це перетин двох або більше дуг, і його номер використовується для посилання на будь-яку дугу, якій він належить. Кожна дуга починається і закінчується або в точці перетину з іншого дугою, або у вузлі, що не належить іншим дугам. Дуги утворяться послідовностями відрізків, з'єднаних проміжними (формотворними) точками. У цьому випадку кожна лінія має два набори чисел: пари координат проміжних точок та номери вузлів. Крім того, кожна дуга має свій ідентифікаційний номер, який використовується для вказівки того, які вузли представляють її початок і кінець, Області, обмежені дугами, також мають ідентифікуючі їх коди, які використовуються для визначення їх відносин з дугами. Далі, кожна дуга містить явну інформацію про номери областей ліворуч і праворуч від неї, що дозволяє знаходити суміжні області. Тобто ми маємо векторну модель даних, яка краще відображає, те як ми, користувачі карт, визначаємо просторові взаємовідносини, записані в традиційному картографічному документі.
GBF/DIME модель
Найбільш відомою є модель GBF/DIME(geographic base file/dual independent map encoding), створена Бюро перепису США для зберігання в комп'ютері вуличної мережі, що використовується під час переписів, що проходять кожні десять років. У ній дуги використовуються для представлення вулиць, річок, рейкових шляхів і т.д. У цій топологічній структурі даних кожна дуга закінчується при зміні напрямку або при перетині з іншого дугою (тобто, не використовуються проміжні точки), а вузли ідентифікуються кодами.
TIGER модель
Деякі проблеми GBF/DIME моделі були усунені з розробкою другої системи, TIGER(topologically integrated geographic encoding and referencing system) створеної для використання в перепису США 1990 року. У цій системі точки, лінії і області можуть адресуватися явно, тому ділянки перепису можуть вибиратися прямо за номером ділянки, а не через інформацію про суміжності, що міститься у зв'язках. Крім того, так як ця модель не покладається не тільки на теорію графів, об'єкти реального світу, такі як звивисті ріки й нерегулярна берегова лінія відображаються графічно більш точно.
POLYVRT
Ще одна модель, розроблена Пьюкером та Крісменом і реалізована пізніше в Гарвардському університеті в лабораторії комп'ютерної графіки називається POLYVRT. Як і TIGER вона усуває не ефективність зберігання та пошуку, властиву базовій топологічній моделі, роздільним зберіганням кожного типу об'єктів (точки, лінії, області). Ці окремі об'єкти потім зв'язуються в ієрархічну структуру даних, де точки через покажчики пов'язані з лініями, а лінії - з областями. Кожен набір відрізків, званий в даній моделі ланцюжком, починається і закінчується в певних вузлах (на пересіку двох ланцюжків). І, як і в GBF/DIME, кожен ланцюжок містить явну інформацію про направлення у формі "Початковий вузол - Кінцевий вузол", а також ідентифікатори правих і лівих областей.
Географічні моделі даних
По суті, моделювання географічної моделі даних включає в себе реальний світ відведений в аналоговій карті в залежності від функції якою ви зацікавлені.
Моделі даних ESRI
Зв'язок геометричних файлів та окремих атрибутів таблиці є загальним для шейпфайлів і покриття та називається «Геореляціонні Дані моделі ESRI”
Растрові моделі
У растрової моделі просторова інформація представлена у вигляді таблиці, кожному осередку якої відповідає заданий колір.Часто растрова модель місцевості використовується як вихідний матеріал для побудови векторних моделей і / або як підкладка для них. Для точного розміщення растру в просторі моделі вказуються координати, як мінімум, одного кута(Або опорної точки) растру. Дуже часто потрібно поєднати кілька растрів,перекривають один одного. При оцифрування наборів об'єктів карти в різні шари корисно використовувати одні і ті ж тіки, щоб шари правильно поєдналися. Растрові моделі зручні для зберігання та аналізу даних, розподілених безперервно на певній площі. Кожна клітинка містить значення, що визначає приналежність до класу або категорії, це може бути вимір або результат його інтерпретації.
Операції над растрами
Алгебра - це математична структура, що складається з двох різних множин елементів, має множину операндів, та множину операцій. Існує ряд аксіом, яким повинна задовольняти алгебра, однак вирішальне значення має замкнутість, інакше кажучи, результат операції над операндом повинен належати множині. Простим прикладом алгебри є множина натуральних чисел з операціями додавання і множення. У алгебри карт операндом є растрова матриця, а операції діляться на чотири класи: локальні, фокальні, зональні і глобальні.
Локальні операції
Локальна операція відображає один растр на інший таким чином, що значення клітинки в новому растрі залежить виключно від значення того ж осередку у вихідному растрі. Приклад локальної операції показаний на малюнку Значення кожного осередку растра встановлюється в 0 або 1 залежно від того, чи перебуває значення тієї ж комірки вихідного растру нижче або вище деякого значення, вказаного користувачем. На цьому малюнку всі комірки, значення яких менше 3, встановлюються в 0, а всі комірки, значення яких дорівнює 3 або перевищує його, встановлюються в 1. Ця операція носить назву установлення порогу, або порогової обробки. Стосовно цифрових карт висоти операція порогової обробки використовується для ідентифікації осередків, розташованих на рівні, що перевищує заданий.
Фокальні операції
При виконанні фокальних операцій значення клітинки нового растру залежить від значень комірки вихідного растру, а також сусідніх з нею осередків. Існують три загальноприйнятих визначення того, що вважати околицями комірки. Всі вони проілюстровані на рисунку. За аналогією з шахами їх називають околицями тури, слона і ферзя. На рисунку значення кожної клітинки нового растру дорівнює сумі значень клітинок вихідного растру, що лежать в ферзевій околиці. Прикладами фокальних операцій над полями є розрахунок ухилу, градієнта, безперервність і т. д. На рисунку показана одна з фокальних операцій, а саме фокальна сума в ферзевій околиці. ція носить назву установченія порогу, або порогової обробки. Стосовно до цифрових картах висоти операція порогової обробки використовується для ідентифікації осередків, розташованих на рівні, що перевищує заданий.
Зональні операції
Значення комірки нового растру при виконанні зональних операцій є функцією значення тієї ж комірки в вихідному шарі, а також значень інших комірок, які знаходяться в зоні, заданій ще одним растром. Наприклад на малюнку значення лівої верхньої комірки нового растру, розміщеного в тій же зоні А, яка вказана на зональній карті. Інакше цю інформацію можна представити в вигляді таблиці, в якій для кожної зони є один рядок, що містить значення суми комірок зони. Як показує приклад, зони не обов'язково повинні бути неперервними і можуть не покривати всі комірки вхідної карти.
Глобальні операції
Глобальні операції відрізняються тим, що значення клітинки в новому растрі - це функція місця розташування або значення всіх клітинок вихідного або іншого растру. На рисунку наведено приклад глобальної операції. У вихідному растрі задано положення джерел S1 і S2. Кожна клітинка нового растру фіксує відстань від даної комірки до найближчого джерела. Дві клітинки, суміжні по вертикалі або по горизонталі, відокремлені один від одного відстанню одиничної довжини, а два відділення, суміжні по діагоналі, розділені відстанню, рівною квадратному кореню з 2.
Гріди
До растрових даних відносять також гріди (grids). Гріди містять розрахункові дані, що часто вигідно використовувати для моделювання та аналізу. Такі дані можуть бути отримані з точок замірів (наприклад, грід хімічного складу грунтів) або засновані на класифікації зображення, наприклад грід землекористування. Гріди також можна створити з векторних даних.
В гріди можуть зберігатися як безперервні дані (наприклад, висота рельєфу), так і категорії (Наприклад, тип рослинності) та додаткові атрибути категорій. Наприклад, в гріді типів рослинності для кожної категорії може зберігатися код, назва типу, придатність для проживання певних видів тварин і код узагальненого типу. У цьому відмінність від векторних даних, де атрибути відповідають окремим об'єктам.
Чим менше розмір комірки растрового шару, тим більше дозвіл і докладніше дані. Однак, оскільки комірки рівномірного гріда покривають всю поверхню, зменшення розміру осередку може істотно збільшити обсяг збережених даних.
Плюси і мінуси растрової і векторної моделей
Моделі TIN
У растрі географічний простір представляється дискретним, кожна клітинка растру займає певну площу. У межах цього дискретного, або квантованого, простору клітинка може мати атрибут абсолютного значення висоти, яке найбільш представницьке для цієї клітинки. Це може бути найвище або найнижче значення або якась середня величина висоти. Таким чином, існуючі растрові структури даних цілком здатні представляти поверхні. Але у випадку векторів картина зовсім інша. Більша частина простору між графічними примітивами лише підрозуміється, а не визначається явним чином. Для визначення цього простору саме як поверхні ми повинні квантувати її якимсь чином, який зберігає важливі зміни поверхової інформації і побічно виявляє області з однаковими даними висоти. Простий спосіб уявити собі це - розглянути як кристалограф описує мінерали. Кожен кристал має набір гладких граней, з'єднаних точками і лініями, які показують значні зміни в його структурі. Аналогічно, ми можемо уявити собі топографічну поверхню у вигляді природного кристала з його плоскими гранями, ребрами і вершинами. Таким чином, ми можемо моделювати поверхню, створюючи послідовності регулярно або нерегулярно розподілених точок. Кожна точка має явно задану висоту. Проводячи через три прилеглі точки площину, ми можемо зобразити трикутну область постійного ухилу. Отримані таким чином трикутники створюють структуру, що представляє по суті "кристалоподібну" модель нашої поверхні. Ця модель, звана нерегулярною тріангуляційних сіткою, дозволяє нам використовувати для опису рельєфу точки деякої сітки. Точки можуть розміщуватися як регулярно, так і нерегулярно. Для одержання моделі поверхні нам потрібно з'єднати пари точок ребрами певним способом, званим тріангуляцією. Тоді, при необхідності отримання тривимірного представлення, TIN може бути показана у вигляді дротяної моделі або моделі з зафарбованими гранями. Крім побудови TIN, точкові дані можуть використовуватися як для традиційного уявлення поверхонь ізоліній. Це особливо елегантний засіб представлення поверхонь насправді використовувався в якості головної структури даних в ранніх системах роботи з даними поверхонь.
Модель TIN відноситься до класу тривимірних векторних моделей та предсталяє собою тріангуляційну нерегулярну сітку (TIN) на поверхні моделювання. TIN-ефективний спосіб зберігання і аналізу поверхонь, так як тріангуляційна мережа дозволяє більш точно, ніж растр, моделювати неоднорідні поверхні, які можуть різко змінювати форму на одних ділянках і плавно - на інших. Це пов'язано з тим, що можна помістити більше точок там, де значення змінюються різко, і менше точок там, де поверхня змінюється плавно. Модель TIN застосовується як спосіб зберігання вхідних даних про поверхні і модель для вирішення завдань на поверхнях у ГІС, що допускають роботу з 3D-моделями.
Модель TIN (Triangulation Irregular Network) - це модель, розроблена спеціально для опису рельєфу. Для побудови TIN можна використовувати будь-яку кількість вхідних даних будь-якого типу (точка, лінія, полігон). При чому кожну таблицю, додану в TIN можна використовувати різними способами - як матриця пікселів, як лінії перегинів, як відтинаючий, заповнюючий, затираючий, або заміщуючий полігони. Модель проста в розумінні і наочна. При правильному використанні вихідних даних - дуже точна. Легко конвертується в грід.
Об'єктно-орієнтована модель
Модель включає мову просторових запитів [Неаlу, 1991] і відображає визнання того факту, що потрібен об'єктно-орієнтований доступ і до БД ГІС і до виконуваних з нею операцій. Ідеї, що лежать в основі цих систем практично ідентичні об'єктно-орієнтованого підходу у програмуванні [Aronson, 1987]. Щодо поняття "об'єктно-орієнтована" не існує загальної угоди, але відомо, що "об'єкт" це є якась сутність, яка має стан, що представляється локальними змінними (цього об'єкту) і набором операцій, які можуть застосовуватися до цього об'єкта. Оскільки кожний окремий об'єкт належить якійсь множині об'єктів і операцій, його можна розглядати як член цього класу (тобто множини, певного одночасного набору локальних змінних і операцій). Кожен з цих класів успадковує властивості від свого Надкласу - подібно до того, як люди успадковують характеристики більш загальної множини, званої ссавцями. У разі ГІС для ілюстрації цієї ідеї можна навести приклад класу об'єктів полігон, який дає кожній області в базі даних всі її властивості (наприклад, списки вузлів, дуг та провінцій, процедури обчислення Центроїд, відображення, накладення полігонів).
Методи зжимання растрових даних
А) Групове кодування
Б) Блочне кодування
В) Ланцюгове кодування
Г) Квадродерево
Д) Ланцюгові коди Фрімена-Хофмена
Групове кодування
Колись растрові дані вводилися в ГІС з допомогою пронумерований прозорої сітки, яка накладалася на карту, яка кодувалась. Кожна клітинка мала чисельне значення, відповідне даними карти, які вводилися (зазвичай з клавіатури) в комп'ютер. Наприклад, для карти розміром 200 х 200 осередків буде потрібно ввести 40'000 чисел. Уявіть, що в кожному рядку існують довгі ланцюжки однакових чисел. Подумайте, скільки часу ви заощадите на одному рядку, якщо б могли сказати комп'ютеру, що, наприклад, з позиції 8 по 56 позицію йдуть одні одиниці, а з 57-й позиції до кінця ряду йдуть двійки. Насправді, ви могли б також зберегти чимало обсягу пам'яті, записуючи тільки початкову та кінцеву позицію для кожного ланцюжку та значення, яке в ній присутнє. У цьому і полягає ідея групового кодування. . Цей метод діє в межах одного рядка растру.
Ланцюгове кодування
Що, якщо б ви могли сказати комп'ютеру почати з окремої комірки зі значенням 1, потім перейти в певному напрямку, скажімо вертикально, на 27 осередків і тоді змінити значення. Це дозволило б кодувати ланцюжки в будь-якому напрямку. Але принцип може бути розширений і далі. Припустимо, що ви бачите велику групу осередків растра, що представляють деяку область. Якщо ви почнете з одного кута, поставивши його координати і значення клітинки, потім перейдете з головних напрямків (вниз, вгору, вправо, вліво) уздовж області, записавши число, яке представляє напрям, і ще одне, дорівнює кількості осередків, на яку ви перемістилися, то для запису області буде потрібно всього лише кілька чисел. Таким чином, ви б зберегли ще більше місця на диску і, звичайно, часу ручного введення. Цей метод називається ланцюговим кодуванням, він буквально прокладає ланцюг осередків растра вздовж кордону кожній області. Загалом, ви вказуєте координати (Х, У) початку, значення комірок для всієї області, а потім вектора напрямків, що показують, куди рухатися далі, де повернути і як далеко йти. Зазвичай вектори описуються кількістю осередків та напрямком у вигляді чисел 0,1,2,3, відповідних руху вгору, вниз, вправо і вліво.
Блочне кодування
Даний метод є модифікацією групового кодування. Замість вказування початкової і кінцевої точок і значення комірок, ми вибираємо квадратну групу осередків растра і призначаємо початкову точку, скажімо, центр або кут, беремо значення клітинки і повідомляємо комп'ютеру ширину квадрата осередків. Як бачите, це, по суті, двомірне групове кодування. Таким чином може бути записана кожна квадратна група осередків, включаючи і окремі осередки, з мінімальною кількістю чисел. Звичайно, якщо ваше покриття має дуже мало великих квадратних груп вічок, цей метод не дасть значного виграшу в обсязі пам'яті. Але в такому випадку і групове кодування може бути неефективним, коли є мало довгих ланцюжків однієї величини. Але все таки більшість тематичних карт мають досить велику кількість таких груп, і блочне кодування тому дуже ефективно.
Квадродерево
Як і блочне кодування, квадродерево засноване на квадратних групах осередків растра, але в даному випадку вся карта послідовно ділиться на квадрати з однаковим значенням атрибута всередині. Спочатку квадрат розміром з всю карту ділиться на чотири квадранти (СЗ, СВ, ЮЗ, ЮВ). Якщо один з них однорідний (тобто містить клітинки з одним і тим же значенням), то цей квадрант записується і більше не братиме участі в розподілі. Кожен квадрант, що залишився знову ділиться на чотири квадранти, знову СЗ, СВ, ЮЗ, ЮВ. Знову кожен квадрант перевіряється на однорідність. Всі однорідні квадранти записуються, і кожен з решти ділиться далі і перевіряється, поки вся карта не буде записана як безліч квадратних груп осередків, кожна з однаковим значенням атрибута всередині. Найдрібніших квадратом є одна клітинка растру. Системи, засновані на квадродереві, називаються системами з змінною роздільною здатністю, так як вони можуть оперувати на будь-якому рівні поділу квадродерева.
Ланцюгові коди Фрімена-Хофмена
Цілі числа від 0 до 7 призначаються восьми векторам напрямків. Метод Фрімена-Хофмена використовує ті ж головні і проміжні напрямки для векторів, що і Гальтон у своїх подорожах для наземної навігації. Призначаючи довжину для кожного вектора, ми можемо записувати окремі лінійні об'єкти, вказуючи їх початок, довжину, напрямок, в якому вони малюються і де вони змінюють напрямок. Існують багато варіації на цю тему, включаючи збільшення кількості кодів до 16-ти або навіть до 32-х для збільшення точності. Результат один - скорочення обсягу векторної БД.
Інструменти просторового аналізу
А) Вибірка Розташування
Б) Просторове Приєднання
В) Буфер
Г) Розкладання (за кольорами, кодами)
Д) Оверлей і витримка інструментів
Вибірка розташування
Для вибірки по розташуванню в меню “выборка” виберіть “Выбрать по расположению”.
Оверлей і витримка інструментів
Всі шари, що мають бути об'єднані в топологічних накладеннях повинні мати ті ж самі параметри географічної прив’язки (карта, проекції, датум, і т.д.).
Накладання полігон на полігон
На даному малюнку ми бачимо об’єднання двох полігонів. При перетинанні формується вузол, що в кінцевому підсумку сприяє створенню нових можливостей полігону.


Крім того, атрибути для кожного з полігонних шарів об'єднуються для створення нової бази даних атрибуту.
Накладання полігон на лінію
Накладання лінії на полігон дозволяє вивчити взаємозв'язок між лінією та особливостями полігону.
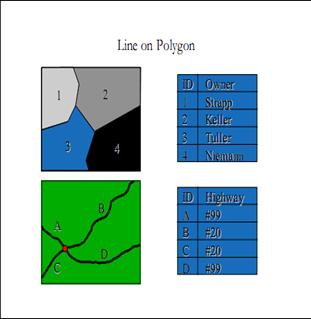
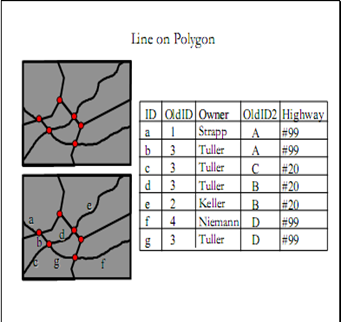
Загальною стратегією для об'єднання атрибутів лінії / полігону є : сегмент повинен призначити для лінійного об'єкта полігону атрибути багатокутника, в середину якого він падає.
Накладання точки на полігон
Накладання точки на полігон дозволяє вивчити взаємозв'язок між точкою та особливостями полігону.
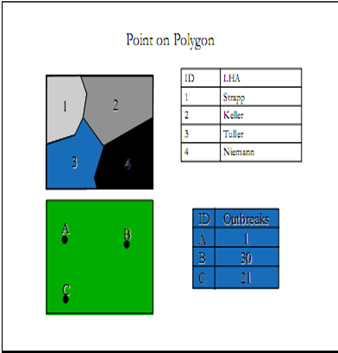
Поєднання атрибутів точки та полігону аналогічне накладенню лінії на полігон.
8. Презентація та додаткові відеоматеріали
Шрифти
Розмір шрифта
Колір тексту
Колір тла
Кернінг шрифтів
Видимість картинок
Інтервал між літерами
Висота рядка
Виділити посилання
Вирівнювання тексту
Ширина абзацу