Лекція 6 Прийняття рішень в умовах визначеності
| Сайт: | Навчально-інформаційний портал НУБіП України |
| Курс: | Майстерність прийняття інженерних рішень` |
| Книга: | Лекція 6 Прийняття рішень в умовах визначеності |
| Надруковано: | Гість-користувач |
| Дата: | понеділок, 7 липня 2025, 17:20 |
Зміст
- 1. Класифікація рішень
- 2. Постановка задачі багатокритеріальної оптимізації.
- 3. Абсолютно-оптимальні оцінки і альтернативи
- 4. Ефективні оцінки і альтернативи
- 5. Слабко ефективні оцінки і альтернативи
- 6. Методи багатокритеріальної оптимізації. Метод ідеальної точки
- 7. Метод послідовних поступок
- 8. Метод послідовного вводу обмежень
- 9. Метод бажаної точки
1. Класифікація рішень
Одною із головних задач і обов’язків керівника є прийняття своєчасних і ефективних рішень, а тому важливою задачею працівників системи контролінгу є своєчасна, об’єктивна та, за можливістю, найбільш повна інформаційна підтримка цього процесу, а також розробка і аналіз альтернативних варіантів управлінських рішень.
Управлінське рішення – це фіксована управлінська дія, яка спрямовує трудовий колектив у напрямку досягнення цілей, поставлених перед організацією.
Для більш повного забезпечення керівника потрібною інформацією, в рамках системи контролінгу пропонується проводити класифікацію майбутніх рішень за певними ознаками
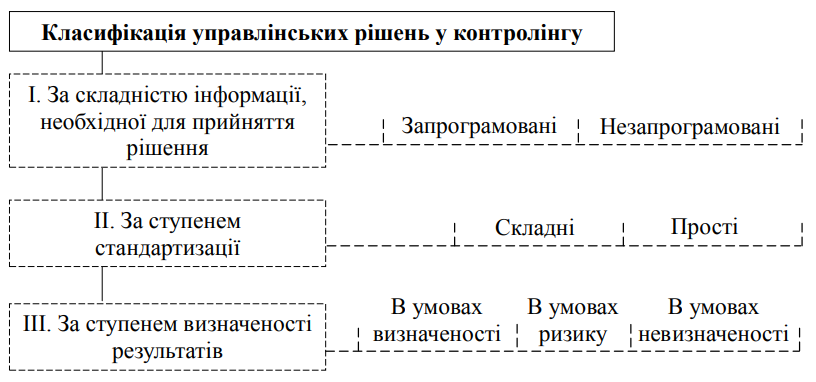
Рис. 1. Класифікація управлінських рішень у контролінгу
За ступенем визначеності результатів виконання кожного з варіантів рішень
Рішення в умовах визначеності – керівник точно знає всі можливі варіанти дій і передбачає результати, які отримає після реалізації кожного варіанту.
Рішення в умовах ризику – керівник точно знає всі можливі варіанти дій і може визначити ймовірність отримання як позитивного, так і негативного результату.
Рішення в умовах невизначеності – керівник не має точної інформації про варіанти дій і не може оцінити ймовірності отримання бажаних результатів.
Критерії прийняття рішення в умовах визначеності передбачає, що варіанти дій є відомі, а також відомими є результати, що мають бути отриманими
Критерії прийняття рішення в умовах ризику передбачає, що варіанти дій є відомі, а також відомими і невідомими є результати, що мають бути отриманими.
Критерії прийняття рішення в умовах невизначеності передбачає, що варіанти дій є невідомі, а також невідомими є результати, що мають бути отриманими.
2. Постановка задачі багатокритеріальної оптимізації.
Задачі і прийняття рішень в умовах визначеності при числовій оцінці наслідків, тобто коли зв’язок між альтернативами й наслідками детермінований (кожній альтернативі відповідає тільки один наслідок) і ціль ототожнюється з максимізацією чи мінімізацією деякої дійсно значної функції, яка визначена на множині всіх наслідків.
Оскільки кожній альтернативі відповідає тільки один наслідок і “корисність” (по відношенню до цілі задачі) цього наслідку оцінюється деякою єдиною числовою оцінкою, а нас цікавить у кінцевому підсумку найкраща оцінка і відповідна їй альтернатива, то можна встановити прямий зв’язок альтернатива – числова оцінка відповідного наслідку, минаючи саме наслідок.
В результаті такого підходу отримаємо дійснозначну функцію f, яка визначена на множині альтернатив і будемо називати її цільовою функцією
Оскільки ціль в задачах і прийнятті рішення при числовій оцінці наслідків полягає у знаходженні такого наслідку, що максимізує чи мінімізує числову оцінку, то під оптимальним розв’язком задачі в умовах визначеності природно розуміти ту альтернативу, яка забезпечує цільовій функції мінімальне чи максимальне значення.
Таким чином, можна зробити висновок: математичною моделлю задачі прийняття рішень в
умовах визначеності при числовій оцінці наслідків є задача оптимізації (максимізації чи мінімізації) дійсної функції, що задана на множині альтернатив.

3. Абсолютно-оптимальні оцінки і альтернативи
В задачах багатокритеріальної оптимізації принцип оптимальності залежить від задання відношення переваги на множині оцінок (від способу порівняння оцінок).



4. Ефективні оцінки і альтернативи
Розглянемо інші відношення переваги на множині оцінок.

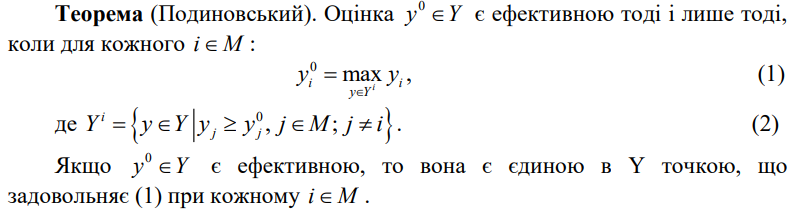

5. Слабко ефективні оцінки і альтернативи
В деяких випадках, зокрема в моделях приняття групових рішень, відношення переваги на множині оцінок Y повинне відбивати “групову думку”, яка агрегує індивідуальні. Очевидно, в різних ситуаціях підсумок порівняння оцінок у і у' може залежати від того, скільки строгих нерівностей виконується при порівнянні їхніх компонент. Однак самим слабким є припущення, яке полягає в тім, що в для всієї групи оцінка у переважніше у' якщо всі нерівності є строгими. Це припущення називається слабкою
аксіомою Парето.



6. Методи багатокритеріальної оптимізації. Метод ідеальної точки
Цей метод не використовує допоміжну інформацію від ОПР про перевагу на множині критеріїв. Це може відбуватися, коли у ОПР ця інформація відсутня або, при наявності, її не можна застосувати з деяких причин.
В цьому випадку робиться припущення про наявність, так званого, "оптимального" розв'язку задачі багатокритеріальної оптимізації, який може бути знайдено шляхом перетворення багатокритеріальної задачі у відповідну скаляризовану (однокритеріальну) задачу.


7. Метод послідовних поступок
Особливістю методу є те, що критерії задачі БКО повинні бути попередньо впорядковані за зменшенням їх важливості, після чого вибір розв'язку задачі здійснюється шляхом виконання
багатокрокової діалогової процедури. Діалогова процедура послідовних поступок складається з одного попереднього і m основних кроків (нагадаємо, що m – це кількість критеріїв).

8. Метод послідовного вводу обмежень
Характерною особливістю цього методу є послідовне (на кожному кроці) введення обмежень на альтернативи, які мають незадовільні, з точки зору ОПР, значення критеріїв.

9. Метод бажаної точки
Особливістю цього методу є необхідність задання ОПР бажаних значень критеріїв для визначення переваги на множині критеріїв.
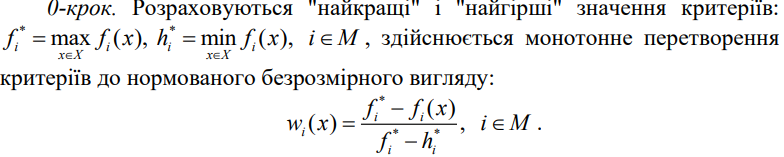

Шрифти
Розмір шрифта
Колір тексту
Колір тла
Кернінг шрифтів
Видимість картинок
Інтервал між літерами
Висота рядка
Виділити посилання