Тема 3. Концептуальніо-наукові засади математичного моделювання бізнес=проєктів
| Сайт: | Навчально-інформаційний портал НУБіП України |
| Курс: | Економетричне моделювання наукових бізнес-проєктів☑️ |
| Книга: | Тема 3. Концептуальніо-наукові засади математичного моделювання бізнес=проєктів |
| Надруковано: | Гість-користувач |
| Дата: | четвер, 5 лютого 2026, 03:15 |
Зміст
- 1. Сутність моделювання як методу наукового пізнання
- 2. Особливості і принципи математичного моделювання
- 3. Структура та особливості побудови економіко-математичних моделей
- 4. Класифікація економіко-математичних моделей
- 5. Основні дефініції економіко-математичного моделювання
- 6. Етапи економіко-математичного моделювання
- 7. Презентація до лекції 3
1. Сутність моделювання як методу наукового пізнання
Модель від лат. («modulus» — зразок, норма, міра.) — це об’єкт, що заміщує оригінал і відбиває його найважливіші риси й властивості для даного дослідження, даної мети дослідження за обраної системи гіпотез.
Математична модель — це абстракція реальної дійсності (світу), в якій відношення між реальними елементами, а саме ті, що цікавлять дослідника, замінені відношеннями між математичними категоріями. Ці відношення зазвичай подаються у формі рівнянь і/чи нерівностей, відношеннями формальної логіки між показниками (змінними), які характеризують функціонування реальної системи, що моделюється.
Сутність методології математичного моделювання полягає в заміні досліджуваного об’єкта його «образом» — математичною моделлю — і подальшим вивченням (дослідженням) моделі на підставі аналітичних методів та обчислювально-логічних алгоритмів, які реалізуються за допомогою комп’ютерних програм. Робота не із самим об’єктом (явищем, процесом), а з його моделлю дає можливість відносно швидко і безболісно досліджувати його основні (суттєві) властивості та поведінку за будь-яких імовірних ситуацій (це переваги теорії). Водночас обчислювальні (комп’ютерні, симулятивні, імітаційні) експерименти з моделями об’єктів дозволяють ретельно та досить глибоко вивчати об’єкт, що недоступно суто теоретичним підходам (це перевага експерименту).
Вже сама постановка питання щодо математичного моделювання будь-якого об’єкта породжує чіткий план дій, який умовно можна поділити на три етапи: модель — алгоритм — програма (рис. 3.1).
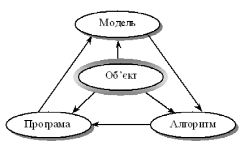
Рис.3.1. Узагальнена схема математичного моделювання
На першому етапі обирається (чи будується) «еквівалент» об’єкта, що відображає в математичній формі найважливіші (ключові) його властивості — закони, яким він підпорядковується, зв’язки, що притаманні складовим його частинам, тощо. Математична модель (чи її фрагменти) досліджуються теоретичними методами, що дає змогу отримати важливі (концептуального характеру) нові знання про об’єкт.
Другий етап — вибір (чи розроблення) алгоритму для реалізації моделі на комп’ютері. Модель подається у формі, зручній для застосування числових методів, визначається послідовність обчислювальних і логічних операцій, котрі необхідно здійснити, щоб отримати шукані величини із заданою точністю.
На третьому етапі створюються програми, що «переносять» модель і алгоритм на доступну комп’ютерну мову. Їх можна назвати «електронним» еквівалентом досліджуваного об’єкта, що є придатним для безпосереднього експериментування на комп’ютері.
Створивши тріаду: «модель — алгоритм — програма», дослідник (системний аналітик) отримує універсальний, гнучкий і відносно дешевий інструмент, який тестується в «пробних» обчислювальних експериментах. Після того як адекватність (достатній рівень відповідності, зважаючи на цілі та прийняту систему гіпотез) тріади щодо досліджуваного об’єкта засвідчена, з моделлю проводять різноманітні та детальні «досліди», які дають нову інформацію про необхідні якісні та кількісні властивості й характеристики об’єкта. Процес моделювання супроводжується поліпшенням та уточненням, за необхідності, всіх складових (ланок) тріади.
Основним інструментальним та ефективним методом дослідження систем є метод моделювання, тобто спосіб теоретичних і практичних дій, спрямованих на створення та використання моделей. Під моделлю можна розуміти образ реального об’єкта (процесу) в матеріальній чи ідеальній формі (тобто такий, який описано знаковими засобами певною мовою), що відображає суттєві властивості модельованого об’єкта (процесу) й заміщує його в ході дослідження й управління.
Метод моделювання ґрунтується на принципі аналогії, тобто можливостях вивчення реального об’єкта не безпосередньо, а шляхом дослідження подібного йому й більш доступного цьому дослідженню об’єкта — його моделі. У подальшому йтиметься лише про економіко-математичне моделювання, тобто про опис соціально-економічних систем знаковими математичними засобами.
Практичними завданнями економіко-математичного моделювання є: по-перше, аналіз економічних об’єктів і процесів; по-друге, економічне прогнозування, передбачення розвитку економічних процесів; по-третє, вироблення управлінських рішень на всіх рівнях господарської ієрархії управління. Однак, не в усіх випадках дані, отримані в результаті економіко-математичного моделювання, можуть використовуватися безпосередньо як готові управлінські рішення, вони можуть розглядатись як «консультуючі» засоби, прийняття управлінських рішень залишається за людиною. Отже, економіко-математичне моделювання є лише однією з важливих компонент у системах аналізу, планування й управління економічними системами, спрямоване на отримання нових знань про об’єкт дослідження.
Одним із важливих аспектів у економіко-математичному моделюванні, як і в інших концепціях моделювання, є поняття адекватності моделі, тобто відповідності моделі модельованому об’єктові чи процесові. Адекватність моделі — дещо умовне поняття, оскільки повної відповідності моделі реальному об’єктові не може бути. Йдеться про відповідність тим властивостям, які вважаються суттєвими для дослідника, відповідають меті дослідження та усталеній системі гіпотез. Зазначимо, що перевірка адекватності економіко-математичних моделей обтяжена складністю вимірювання економічних величин, але без такої перевірки застосування результатів моделювання в аналізі та управлінських рішеннях може не лише виявитися малокорисним, а й призвести до негативних наслідків.
Основні характеристики економіко-математичних моделей. Економіко-математичні моделі вирізняються серед інших математичних моделей тим, що об’єктом моделювання є економічні процеси, а сама модель відображає економічні взаємозв’язки та відносини, що існують у реальній дійсності (в реальних процесах та явищах). Здійснюючи ідентифікацію та інтерпретацію економіко-математичних моделей, використовують економічні показники.
Кожна економіко-математична модель реального явища характеризується:
а) об’єктом моделювання;
б) системним описом об’єкта;
в) цілями щодо побудови моделі;
г) принципами моделювання;
д) апаратом моделювання;
є) способами ідентифікації й інтерпретації результатів.
Об’єктом моделювання може бути або реальна господарська система, або один чи кілька процесів, що розвиваються в такій системі. Для побудови моделі треба не просто вказати найменування об’єкта, а й дати його опис у вигляді системи, тобто виявити суттєві грані його взаємодії із зовнішнім середовищем, його структуру. Моделі, що відображають (заміщують) один і той самий об’єкт з різних поглядів, слід вважати різними.
Нагадаймо також, що поняття адекватності моделі має кілька різних граней. По-перше, можна вести мову про адекватність моделі щодо досліджуваного реального процесу, розуміючи під цим ступінь відповідності його характеристик характеристикам об’єкта. По-друге, потрібно оцінювати адекватність моделі щодо поставленої задачі (цілей).
Апарат моделювання визначається типом математичних конструкцій, що використовуються для побудови моделі. Найпоширенішими є моделі, побудовані за допомогою апарату лінійної алгебри, регресійного аналізу, лінійних диференційних рівнянь. Інколи кажуть про специфічний апарат — «апарат виробничої функції». Вибір того чи іншого апарату економіко-математичного моделювання значною мірою ґрунтується на гіпотезах, що покладені в основу побудови моделі.
Як зауважувалось вище, соціально-економічні системи належать, як правило, до так званих складних систем, яким притаманна низка властивостей, що треба враховувати в їх моделюванні, інакше неможливо твердити про адекватність побудованої моделі. Серед цих властивостей зазначимо, зокрема, такі: емерджентність як прояв у найяскравішій формі властивості цілісності системи, тобто наявність у економічної системи таких властивостей, які не є притаманними жодному з її елементів, котрий розглядається окремо, поза системою. Емерджентність — це результат виникнення між елементами системи так званих синергетичних зв’язків, які забезпечують збільшення загального ефекту до більших обсягів, ніж сума ефектів окремо взятих елементів системи, що діють (функціонують) незалежно. Тому соціально-економічні системи потрібно досліджувати й моделювати зважаючи на синергізм; динамічність економічних процесів, що полягає в зміні у часі параметрів і структури економічних систем під впливом як внутрішніх, так і зовнішніх чинників (навколишнього середовища); невизначеність щодо розвитку економічних явищ (процесів).
Економічні явища та процеси мають нелінійний, випадковий характер. Невизначеність іманентно притаманна економічним системам, тому для вивчення їх потрібно застосовувати економіко-математичні моделі на базі теорії ймовірностей і математичної статистики, а також на базі теорії нечітких (розпливчастих) множин тощо. Важливою також є розбудова ризикології (науки про економічний ризик) тощо; неможливість ізолювати процеси, котрі здійснюються в економічних системах незалежно від процесів у навколишньому середовищі, з тим щоб спостерігати та досліджувати їх окремо; активна реакція на нові чинники, що з’являються.
В економіці неможливо використовувати моделі подібності, неможливо побудувати точну копію економічної системи в масштабі і на ній моделювати різні варіанти економічної політики. В економіці можливості локальних економічних експериментів гранично обмежені, оскільки всі її складові тісно взаємопов’язані, а отже, «чистий» експеримент є практично неможливим. Залишається спиратися на власний досвід, досвід інших країн, безпосередні експерименти зі всією економікою та на математичне моделювання, але з обов’язковою адаптацією до конкретних умов. Разом з тим неможливо безпосередньо передбачити середньо- та довготермінові наслідки окремих рішень, це можна зробити лише на підставі концептуальних моделей розвитку економіки, що спираються на минулий досвід. У свою чергу концептуальні моделі, власне, і становлять фундамент математичних моделей.
Економіка як складна система є підсистемою суспільства, але у свою чергу вона складається з виробничої і невиробничої сфер (господарських одиниць), які взаємодіють між собою. Сутність взаємодії між суспільством та економічною системою визначає двоїсту роль людини у суспільному виробництві — як агента виробничого процесу, тобто як об’єкта і як суб’єкта, заради котрого цей процес, власне, і здійснюється. Кожна особа виконує подвійну роль: з одного боку, як споживач, а з другого — як виробник. Окрім робочої сили (носія знань та вмінь) матеріальними ресурсами є природні ресурси (зокрема земля, енергія сонця) та засоби виробництва.
Створення теорії аналізу й управління економікою передбачає: виявлення об’єктивних закономірностей взаємодії (взаємозв’язків) економічної системи із суспільством і біологічним середовищем та внутрішньої організації системи; формалізацію опису цих взаємозв’язків у категоріях цілеспрямованої раціональної поведінки тощо.
Засоби виробництва поділяються на засоби праці, котрі беруть участь у кількох виробничих циклах, аж до заміни їх унаслідок морального старіння чи фізичного зношення, та предмети праці, які задіяні в одному виробничому циклі. Особливе (двоїсте) місце серед засобів виробництва займає земля. Накопичені засоби виробництва (виробничі засоби) складаються з основних виробничих і обігових засобів. Основні виробничі засоби (ОВЗ) протягом тривалого часу обслуговують процес виробництва, зберігаючи свою натуральну форму й зношуючись частково, беруть участь в утворенні вартості виробленого в поточному році продукту. Просте відтворення (відновлення) основних виробничих засобів здійснюється за рахунок амортизаційних відрахувань, розширене — за рахунок капітальних вкладень та, частково, амортизаційного засобу.
Оборотні засоби — предмети праці. Вони деталізуються як виробничі запаси та предмети праці, котрі, зокрема, входять до незавершеної продукції. У результаті функціонування економіки протягом року всі галузі матеріального виробництва створюють валовий внутрішній продукт (ВВП). У натурально-речовій формі ВВП поділяється на засоби праці та предмети споживання, а у вартісній — на фонд заміщення основних засобів (амортизаційний фонд) і новостворену вартість (національний дохід). У процесі створення ВВП виробнича підсистема економіки виробляє та споживає проміжний продукт. За матеріально-речовим складом проміжний продукт — предмети праці — використовується в поточному виробничому споживанні, а його вартість переходить у вартість засобів праці чи предметів споживання, що входять до ВВП.
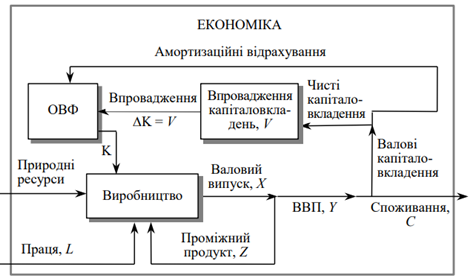
Рис. 3.2. Потоки продуктів і ресурсів в економіці
На рис. 3.2 наведена схема процесів виробництва, розподілу, накопичення та споживання. Проміжна продукція — це паливо, енергія, сировина, матеріали, комплектувальні вироби тощо. Зазначимо, що не існує абсолютно чіткої межі між проміжним продуктом і предметом споживання. Наприклад, цемент, проданий населенню, належить до предметів споживання, а цемент, закуплений будівельним підприємством, — до проміжної продукції.
У сучасному суспільстві роль специфічного товару — загального товарного еквівалента — виконують гроші. Фінансово-кредитні установи (державні та комерційні банки, їхні філії, страхові компанії, різноманітні засоби тощо) спільно з фінансово-бухгалтерськими службами господарських комірок утворюють фінансово-кредитну підсистему економічної системи. Нематеріальним ресурсом поряд з фінансовим виступає соціально-інтелектуальний потенціал суспільства. Основу економічної системи становлять виробничі комірки. Це заводи, фабрики, шахти, родовища, електростанції, сільськогосподарські та інші виробничі підприємства й фірми, наділені господарською самостійністю.
З організаційно-господарського погляду виробнича комірка — це самостійна господарська одиниця, котра наділена правом юридичної особи, функціонує за рахунок власних коштів (засобів), відносно самостійно розпоряджається своїми ресурсами (засобами виробництва, робочою силою та фінансовими засобами) і виробленою продукцією. Як самокерована система виробнича комірка складається з керованого об’єкта (робоча сила та виробничий апарат) та керуючої системи (дирекція, функціональні служби, наглядова рада тощо). Коли окремі виробники в межах суспільства почали виготовляти різні предмети споживання та обмінюватися ними між собою, виник ринок. Отже, ринок — наслідок, результат поділу праці.
У сучасному світі не існує жодної країни, в якій держава не регулювала б (м’яко чи жорстко, прямо чи опосереднено) діяльність господарських комірок. М’яке, опосереднене регулювання за допомогою ринкових важелів свідчить про високий ступінь розвитку ринкової економіки в даній країні. Виробничі комірки і виробничо-технологічні зв’язки між ними утворюють виробничо-технологічну структуру економічної системи. Ненадійність у виробничо-технологічній взаємодії виробничих комірок, конкуренція на ринках товарів, грошей та робочої сили — об’єктивна основа для утворення об’єднань господарських одиниць (асоціацій, концернів, корпорацій тощо). Утворення об’єднань потребує, у свою чергу, регулюючої функції держави, яка в інтересах споживачів повинна не допускати надмірного монополізму на ринках товарів і послуг, а також на ринках робочої сили та грошей.
Організаційно-господарська структура економічної системи — це сукупність господарських одиниць та організаційно-господарських зв’язків між ними. Якщо виробничо-технологічні зв’язки є горизонтальними, то організаційно-господарські — вертикальними. Її (цю структуру) можна уявити як багатоповерхову надбудову над виробничо-технологічною структурою.
Перший поверх — орган управління господарських одиниць і прямі вертикальні зв’язки кожного органу управління зі своєю керованою одиницею.
Другий поверх — орган управління об’єднань і вертикальні зв’язки з органами управління відповідних бізнесових одиниць.
Третій поверх — центральні органи управління економічною системою та вертикальні їх зв’язки з органами управління першого та другого поверхів.
Використовуючи системний підхід щодо дослідження економіки на підставі математичних моделей, виокремлюють, зокрема, макро- та мікроекономічні моделі. Перші відображають функціонування та розвиток усієї економічної системи чи її великих підсистем, другі — господарських одиниць і одиниці є неподільними, але коли досліджуються мікромоделі, то бізнесова одиниця, у свою чергу, може розглядатись як складна система. До великих підсистем можна віднести: перший і другий підрозділи національної економіки, галузі національної економіки, міжгалузеві комплекси.
Під першим підрозділом мають на увазі сукупність господарських одиниць, що виробляють засоби виробництва, під другим — предмети споживання. Нерідко перший підрозділ деталізують на два сектори: нульовий, де виробляються паливо, енергія, сировина, матеріали (тобто предмети праці), та перший, у якому виробляються засоби праці. Часто під сектором розуміють виробничу підсистему економіки, що виробляє один агрегований продукт. У галузь виокремлюють виробничі одиниці, що є відносно однорідними за використовуваною сировиною, технологією, вироблюваною продукцією, професійним складом виробничого персоналу. Стосовно до моделювання, то тут під галуззю розуміють «чисту» галузь, що виробляє лише один продукт. Наприклад, галузь сільського господарства — виробництво збіжжя як одного продукту, хоча, як зрозуміло, збіжжя є узагальненим поняттям — це зерно і пшениці, і жита, і рису, ячменю, вівса, кукурудзи, проса, гречки, маку тощо. Галузь електроенергетики виробляє один продукт — електроенергію, хоча можна розрізнити: гідро-, тепло-, атомну тощо. Окрім звичайних галузей, розглядаються також великі галузі національної економіки: промисловість, будівництво, транспорт, зв’язок, торгівля тощо. Міжгалузевий економічний комплекс — це сукупність галузей, підгалузей і виробництв, що перебувають у тісних виробничо-технологічних зв’язках і реалізують важливу національну мету (наприклад, паливно-енергетичний комплекс забезпечує суспільство й економіку паливом та енергією; агропромисловий комплекс — продовольством і сільськогосподарською сировиною).
Легко дійти висновку, що економіка належить до класу складних систем. Можливості, навіть кваліфікованого колективу фахівців, відтворити на вербально-логічному рівні картину поведінки економічних об’єктів (об’єктів керування), що перебувають під впливом великої кількості внутрішніх та зовнішніх чинників, досить обмежені. Тому доводиться залучати на допомогу математичні моделі, котрі доповнюють логіко-описові уявлення щодо поведінки економічних об’єктів і процесів. Існує й відповідний досвід, що має свою досить тривалу (не одного століття) історію.
Проте, визнання об’єктивності ринку та ейфорія з приводу його всемогутності як творця загального щастя — речі різні. Ще з часів Адама Сміта точаться суперечки, виникають колізії між економічними теоріями відносно доцільності втручання держави в економічні процеси. Звичайно, соціалістичне жорстке планування, як і лібералізм (усунення держави від регулювання економіки), — це крайнощі. Міра державного втручання залежить від конкретних обставин. Так, зокрема, у періоди системних трансформацій соціально-економічних процесів роль державного регулювання, на нашу думку, суттєво зростає. Механізм ринкових відносин є ефективним у багатьох сферах економічного буття, але є й сфери, де ринковий механізм безсилий. Більше того, буквальне використання ринкової логіки у цих сферах може призводити до критичної ситуації.
Ринкові механізми не можуть правильно зорієнтуватися в пошуках ефективних рішень у ситуаціях: 1) монополії чи олігополії; 2) значного розриву в часі між витратами й економічним ефектом (лаг — затримка реалізації значних за обсягом інвестицій); 3) зниження додаткових витрат на приріст виробництва продукції за спадаючих цін (ефект науково-технічного прогресу) тощо. Головний «ворог» ринкових механізмів як механізмів організації ефективного функціонування економіки — це, звичайно, монополія. Спробуймо описати математичною мовою колізії, що виникають у разі зіштовхування ринку, його механізмів, з монополією.
Приймемо гіпотезу, згідно з якою економічна система спрямована до максимізації сумарного економічного ефекту (PS), тобто сумарного прибутку:
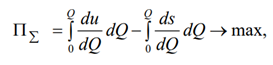
де Q — випуск продукту; u(Q) — функція валового економічного ефекту (корисності); du/dQ — приріст валового економічного ефекту (корисності) від кожної додаткової одиниці продукції; s — витрати на виробництво; ds/dQ — приріст витрат на виробництво додаткової одиниці продукції.
Перший елемент правої частини цього виразу характеризує валовий економічний ефект, другий — витрати на виробництво всього обсягу продукції, а вираз у цілому — сумарний економічний ефект (продукт). Легко помітити, що розширення виробництва буде доцільним лише доти, доки додаткові витрати не зрівняються з додатковим валовим економічним ефектом від споживання. Математично це положення доводиться дослідженням наведеного вище виразу (1.7) на максимум. Якщо продиференціювати PS по Q і похідну прирівняти до нуля, то оптимальний обсяг виробництва, який забезпечує максимум сумарного прибутку, відповідатиме точці Q, у якій ds/dQ = du/dQ , тобто додатковий валовий ефект споживання дорівнює додатковим витратам на виробництво одиниці продукції. Звичайно, тут повинні виконуватись умови:
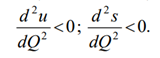
Але в умовах ринкової економіки відбувається розподіл сумарного економічного ефекту між виробником продукції, її споживачем і бюджетом. Характер цього розподілу значною мірою визначає зацікавленість економічних суб’єктів у досягненні суспільної ефективності, тобто в русі виробництва до точки оптимуму. У чому ж полягають економічні інтереси виробника (l) і споживача (с)? Очевидно, що виробник зацікавлений у максимізації різниці між обсягом реалізації по ціні p та витратами:
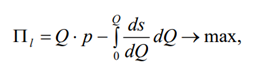
де Pl — прибуток виробника.
Споживачеві важливо максимізувати різницю між економічним ефектом від використання продукції та ціною за неї:
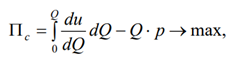
де Pc — прибуток споживача.
Якщо виробник не є монополістом, тобто не в змозі вплинути на рівень цін (вільна конкуренція), то p — не залежить від Q, тобто максимум ефекту виробника буде досягнутий у точці, де похідна Pl по Q дорівнюватиме нулеві, тобто коли: p = ds / dQ , а максимум ефекту споживача — в точці, де: p = du / dQ Максимум сумарного ефекту досягається за обсягів виробництва (Qopt), котрі характеризуються співвідношенням
du/dQ =ds/dQ
Звідси можна зробити висновок, що виробник буде зацікавлений у виробленні оптимального, з погляду народного господарства, обсягу продукції (Qopt), а споживач — у повному використанні цієї продукції за умови, коли ціни встановлюються на рівні: popt = du/dQ =ds/dQ
Але
якщо виробник контролює значну частку ринку (випуску продукції, галузі) і йому
надається право впливати на визначення обсягів випуску продукції, то його
інтереси розходяться з народногосподарськими інтересами. Формально цю
суперечність можна показати таким чином. Якщо p = f (Q), то . 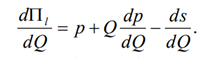
Споживачі
не в змозі вплинути на обсяги та ціну. Тобто максимум ефекту виробника буде
досягнуто за умови: 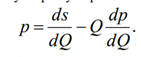
Отже, цей результат свідчить про те, що за можливості контролювати значну масу продукції з боку виробника точка його локального оптимуму не збігається з точкою народногосподарського оптимуму. Раціональною є гіпотеза щодо від’ємної еластичності цін та обсягу виробництва (зі зростанням обсягів виробництва ціни на продукцію знижуються), тобто dp/dQ < 0 .
Виробник,
прагнучи до максимізації свого локального критерію, буде здебільшого
зацікавлений у заморожуванні виробництва на рівні, нижчому, ніж оптимальний (Ql
< Qopt), і, відповідно, у завищенні цін pl >
p* opt , оскільки 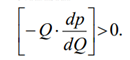
За подібних умов державне регулювання економіки повинно забезпечити таку організаційну систему функціонування господарських об’єктів, яка використовувала б ефективні методи вилучення доходів у великих виробничих 35 об’єднань (монополій) або їх недопущення. Тобто державне регулювання економіки в даному випадку є необхідним.
2. Особливості і принципи математичного моделювання
Головна особливість моделювання полягає у тому, що це метод опосередкованого пізнання за допомогою об’єктів-заміщувачів. Саме ця особливість моделювання визначає специфічні форми використання абстракцій, аналогій, гіпотез, інших категорій і методів пізнання.
Сформулюємо принципи, які визначають загальні вимоги, яким повинна задовольняти правильно побудована математична модель деякого об’єкта (системи).
Принцип 1. Полярність діалектичної пари «модель — об’єкт». Ця діалектична пара завжди полярна, має два полюси — «модель» і «об’єкт».
Принцип 2. Первинність об’єкта. З двох взаємно пов’язаних полюсів діалектичної пари «модель — об’єкт» один із них (об’єкт) є первинним, інший (модель) — похідним від нього.
Принцип 3. Зумовленість моделі об’єктом. Наявність полюсу «модель» зумовлює необхідність наявності полюсу «об’єкт».
Принцип 4. Множинність моделей щодо об’єкта дослідження. Як «модель» для об’єкта, так і «об’єкт» для даної «моделі» семантично та інтерпретаційно багатозначні: «об’єкт» описується не однією, а багатьма «моделями», «модель» віддзеркалює властивості не одного, а багатьох «об’єктів».
Принцип 5. Адекватність. Цей принцип передбачає відповідність моделі меті дослідження, прийнятій системі гіпотез за рівнем складності й організації, а також відповідність реальній системі (об’єкту). Доки не вирішено питання, чи правильно відображає модель досліджувану систему (об’єкт), цінність моделі незначна.
Принцип 6. Спрощення за умови збереження суттєвих (ключових) властивостей об’єкта (системи). Модель повинна бути в деяких аспектах суттєво простішою від прототипу — в цьому власне й полягає сенс моделювання, тобто модель ігнорує несуттєві властивості об’єкта. Цей принцип може бути названий принципом абстрагування від другорядних деталей.
Практичні рекомендації щодо зменшення складності моделі:
· зменшення кількості змінних за допомогою виключення несуттєвих змінних або їх об’єднання. Процес перетворення (редукції) моделі в модель з меншою кількістю змінних і обмежень називають агрегуванням;
· зміна природи змінних величин й параметрів. Змінні величини й параметри наближено розглядаються як постійні, дискретні — як неперервні тощо;
· зміна функціональної залежності між змінними. Нелінійна залежність замінюється зазвичай лінійною, дискретна функція розподілу ймовірностей — неперервною тощо;
· зміна обмежень (збільшення, виключення чи модифікація). Після зняття обмежень одержуємо оптимістичне рішення, після введення — песимістичне. Варіюючи обмеженнями, можна знайти можливі граничні значення ефекту чи ефективності. Такий спосіб часто застосовують для знаходження попередніх оцінок ефективності рішень на етапі постановки задач;
· обмеження точності моделі. Точність результатів моделі не може бути вищою за точність вхідних даних.
Принцип 7. Блочна побудова. За дотримання цього принципу блочної побудови полегшується розроблення складних моделей і з’являється можливість використання накопиченого досвіду та адаптації готових блоків із мінімально необхідними зв’язками між ними. Виокремлення блоків відбувається з урахуванням розподілення моделі за етапами й режимами функціонування об’єкта (системи).
Складні об’єкти (системи) потребують розроблення цілої ієрархії моделей. Виокремлюють такі рівні: вся система, підсистеми, підсистеми керування тощо.
Існують різні форми зображення математичної моделі. Найтиповіші групи їх різновидів — інваріантна, алгоритмічна, аналітична, схемна.
Інваріантна форма
— зображення математичної моделі безвідносно до методів, за допомогою яких може
розв’язуватись поставлена задача моделювання. Приклад інваріантної форми: 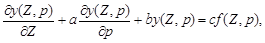
де а, b, c — відомі характеристики об’єкта; f(Z, p) — відома функція; y(Z, p) — невідома функція.
Алгоритмічна форма — зображення математичної моделі у вигляді послідовності дій, які необхідно виконати, щоб при розв’язанні поставленої задачі моделювання перейти від відомих даних до шуканого результату. Приклад алгоритмічної форми:
1. Визначити значення характеристик об’єкта a, b, c.
2.
Обчислити d: 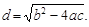
3. Якщо d ³ 0, то обчислення значення результату (х, у):
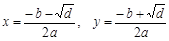 .
.
Аналітична форма — зображення математичної моделі у вигляді формул та співвідношень між математичними виразами, за допомогою яких шукані в задачі моделювання результати визначаються через відомі дані. Приклад аналітичної форми:
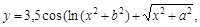
де a, b — відомі характеристики об’єкта, х — змінна, у — результат.
Схемна форма — зображення
математичної моделі у вигляді таблиць даних, діаграм, схем, графів, графіків.
Приклад схемної форми: 
Тут F1, F2 — передаточні функції об’єкта.
Використання аналогів у побудові моделей. Аналоги в побудові моделей використовуються у величезній кількості випадків: або за спроби побудувати модель деякого об’єкта, або коли неможливо прямо вказати фундаментальні закони чи варіаційні принципи, котрим він підпорядковується, або коли з погляду наших сьогоденних знань взагалі немає впевненості в існуванні подібних законів, що допускають математичну формалізацію. Одним із плідних підходів до такого роду об’єктів є використання аналогів з уже вивченими явищами.
Наголосимо, що використання математичних методів в економічному аналізі жодною мірою не зводиться до підбору прийнятих формул, підстановки в них певних чисел та певного чаклування, в результаті чого виходить «відповідь». Нагадаємо рекомендації відомого американського вченого Р.Хемінга: «Мета обчислень — розуміння, а не числа»; «перш ніж розв’язувати задачу, подумай, що робити з її розв’язком».
3. Структура та особливості побудови економіко-математичних моделей
У сільському господарстві взаємозв’язки в економічних процесах характеризують перетворення виробничих ресурсів в готову продукцію. Для вивчення процесів управління ефективною організацією цих перетворень створюються моделі, до яких застосовують методи мислення по аналогії. Таким чином, модель є загально методологічне наукове поняття, яке застосовують в різних галузях науки і техніки. Вона має важливе значення для дослідження економічних проблем при необхідності глибокого проникнення у специфічність об’єктів, що вивчаються. Між моделлю і досліджуваним економічним процесом, повинно означати сходність, а не їх тотожність. Модель, відтворюючи реальний економічний процес, спрощує його, відволікається від ряду його непринципових рис. Тому модель – це умовний образ, який абстрактно відображає основні взаємозв’язки, які існують в реальному економічному процесі. В моделях відбувається абстрагування не тільки від несуттєвих зв’язків, але і від якості предметів і конкретного значення величин. Всі суттєві характеристики і властивості об’єкту чи процесу, що вивчається записуються за допомогою алгебраїчних формул, частіше за все, це рівняння або нерівності. Запис всіх характеристик і властивостей економічного процесу у вигляді алгебраїчних формул називають економіко-математичною моделлю. Таким чином, під структурною економіко-математичною моделлю слід розуміти концентрований вираз суттєвих зв’язків і закономірностей процесу функціонування економічної системи в математичній формі.
При кібернетичному тлумаченні економіко-математичної моделі умови задач, що вирішуються, будуть представляти собою вхідну інформацію або параметри управління. Зміни цих параметрів, в процесі вирішення задачі, будуть характеризувати зміну стану досліджуваного об’єкту, а екстремум цільової функції буде являтись критеріальним показником досягнення системою оптимального стану. В економіко-математичних моделях параметри зазвичай надаються у вигляді таблиць чисел, які пов’язані в єдину систему функціональних рівнянь різного типу.
Найбільш поширеними в практиці досліджень є економіко-математичні моделі, які представлені балансовими і оптимізаційними моделями. Балансові, як правило, характеризуються системою балансових таблиць, які мають форму шахового балансу і можуть бути записані у вигляді квадратної матриці. Оптимізаційні моделі відрізняються від балансових тим, що метою їх побудови є не стільки описування структури економічної системи, скільки математичне описування умов її функціонування. Якщо перші моделі, в основному, повинні задіяти звітний матеріал, то оптимізаційні широко використовують планово-нормативну інформацію.
Моделі розробляють структурні і розширені. В структурній моделі зв’язки і закономірності економічної системи інтерпретують в математичній формі. Розширена економіко-математична модель містить звітний і планово-нормативний матеріал, який описує умови функціонування економічної системи. Така модель оформляється у вигляді матриці.
Економіко-статистичні моделі представляють собою кореляційне рівняння зв’язку залежної змінної величини (Y) і однією або декількох незалежних змінних величин (факторів) Хі. За допомогою таких рівнянь визначають кількісну міру впливу факторів (Xі) на результативний показник (Y). За допомогою робочого рівняння визначають теоретичні або прогнозні значення результативного показника, та проводять факторний аналіз відповідного показника.
Як приклад економічної моделі розгляньмо спрощений (ідеалізований) варіант так званої «павутиноподібної моделі», яка описує процес формування попиту і пропозиції певного товару чи виду послуг на конкурентному ринку (випадок досконалої конкуренції). Ідеться про формалізацію економічного закону попиту та пропозиції, згідно з яким: кількість товару, що його можна продати на ринку (тобто попит), змінюється у напрямку, протилежному зміні ціни товару; кількість товару, який виробляють і доставляють на ринок (тобто пропозиція), змінюється у тому самому напрямку, що й ціна; водночас реальна ринкова ціна формується на рівні, на якому попит і пропозиція наближено дорівнюють одне одному (приблизно збігаються з деякою заданою точністю), тобто перебувають у рівновазі.
Першим, хто спробував математично сформулювати цей закон, був французький учений А. Курно. Подамо математичну формалізацію положень цього закону. Нехай Xt — ціна товару в момент часу t, а Dt і St — кількість товару, купленого і пропонованого відповідно на ринку в той самий момент часу t. Тоді, з урахуванням одного інтервалу часу, необхідного виробникам-продавцям для того, щоб «зреагувати» на ціну X, можна математично сформулювати наведені закономірності:
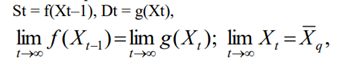
де f(X) — деяка монотонно зростаюча і g(X) — монотонно спадна функції від аргумента X (тобто від ціни), Xq — рівноважна ціна.
Математичні співвідношення, що відображають закон попиту і пропозиції, можуть бути проілюстровані. Як бачимо на рис. 1.2, процес формування рівноважної ціни почався з призначення в перший (початковий) момент часу ціни на рівні X1. Продовження цього процесу (індексовано стрілками) павутиноподібно прямує до точки перетину кривих g(X) і f(X).
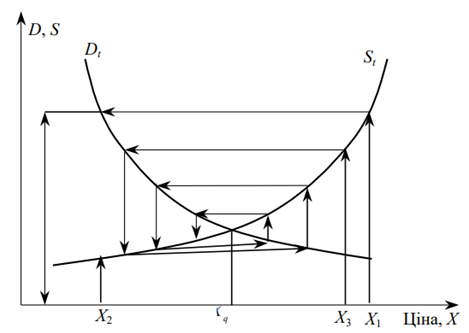
Рис. 3.3. Графік процесу формування попиту і пропозиції
Реальна модель закону попиту і пропозиції, звичайно, складніша. Зокрема, D і S залежать не лише від ціни X. Крім цього, зв’язок (наближений) між D і S, з одного боку, і ціною X — з другого, має не детермінований, а стохастичний характер. Щоб описана вище модель з економічної перетворилася в економетричну, потрібно вести мову не взагалі про закон попиту і пропозиції, а про конкретну дію його в даному секторі економіки в певний час і стосовно конкретного товару (чи виду послуг). Відповідно, конкретизація виду функцій g(X) і f(X), повинна проводитися на підставі статистичних даних щодо значень Xt, St, Dt, де tÎ{1,...,T}, Т — кількість періодів, протягом яких здійснювався моніторинг і отримані дані.
Приклад «Павутиноподібної моделі» фірми
Підприємець збирається вкласти кошти у створення фірми, яка випускатиме товар і реалізовуватиме його на ринку. Його цікавить, як буде поводити себе ціна товару за змін обсягів виробництва. Він розуміє, що при збільшенні обсягів виробництва ціна одиниці товару спадатиме. Йому важливо знати, за яких умов ціна буде стабільною. У науковій літературі описано кілька варіантів відповідної моделі. У них приймається низка гіпотез, зазвичай припускається, що попит на деякий продукт упродовж певного (заданого) проміжку часу залежить від ціни (та інших чинників) на цьому проміжку. Що стосується пропозиції, то вона визначається цінами попереднього проміжку часу (тиждень, місяць, квартал тощо). Окрім цього, приймається гіпотеза, згідно з якою ринок перебуває в умовах локальної рівноваги. Як уже зазначалось, історично така модель отримала назву «павутиноподібної».
Аналіз і розв’язання
Існують як мінімум чотири варіанти відповідної моделі: детермінована, стохастична, модель з навчанням та модель із запасами. У детермінованій моделі відсутнє урахування випадкових чинників. У стохастичній моделі враховується вплив на попит непередбачуваних коливань уподобань і доходів споживачів, а також інших випадкових чинників, які впливають на попит. Пропозиція на попередньому проміжку часу також вважається залежною від впливу випадкових чинників, усі вони відображають вплив коливань у технологічному процесі тощо. Умова локальної рівноваги означає збіг (незначну різницю) попиту і пропозиції з точністю до певної заданої величини.
У моделі з навчанням приймається гіпотеза, за якою постачальники (виробники), ураховуючи тенденцію зміни цін, планують випуск продукції на наступний проміжок часу. В останніх двох моделях ціни встановлюються на такому рівні, щоб забезпечити локальну рівновагу лише за рахунок поточного виробництва, і жодних запасів продукції не створюється (зокрема, тому що продукція швидко псується). У модель із запасами вводиться додаткова група учасників ринкового механізму, котрих можна назвати комерсантами. Вони тримають запаси та організовують торгівлю.
Приклад стохастичної моделі.
Припустимо, що попит на t-му проміжку часу лінійно залежить від поточної ціни (це припущення не є обов’язковим. Навпаки, воно досить жорстке. У реальних процесах припускається, що така залежність буде нелінійною. Вид залежності визначається на підставі застосування економетричних методів і моделей). Окрім цього, вважатимемо, що попит на ринку має випадковий розкид. Для формалізованого опису необхідно в наших припущеннях обчислити на підставі доступної інформації відповідно оцінки коефіцієнтів лінійного рівняння та похибку як випадкову величину, що має певний закон розподілу. У результаті відповідних обчислень можна отримати, зокрема, такий вираз:
Dt = A – BXt + ut,
де Dt — попит на t-му проміжку часу; A, B — коефіцієнти лінійної регресії (В > 0); Xt — ціна одиниці продукції на t-му проміжку часу; ut — випадкова величина, що має заданий закон розподілу.
Логічно припускати, що попит симетрично коливається відносно деякого середнього значення, котре визначається постійними коефіцієнтами лінійного рівняння (їхніми оцінками). Тому, зокрема, можна обрати нормальний закон розподілу з нульовим математичним сподіванням і заданим середньоквадратичним відхиленням su.
Припустимо, що пропозиція впродовж поточного проміжку часу також лінійно (в середньому) залежить від ціни, але не поточної, а такої, що являє собою комбінацію цін на двох попередніх проміжках часу. У найпростішому випадку це може бути середнє значення цін протягом двох попередніх проміжків часу. Отже, для обчислень пропозиції можна (якщо для цього є підстави) використовувати таку залежність:
St = C + KX(r) + vt ,
де St — пропозиція впродовж t-го проміжку часу; C, K — коефіцієнти лінійної регресії (K > 0); X(r) — середнє (середньозважене) значення ціни на двох попередніх проміжках часу; vt — випадкова величина, що має заданий закон розподілу.
Можна, зокрема, для спрощення обрати нормальний закон розподілу випадкової величини vt з нульовим математичним сподіванням і заданим середньоквадратичним відхиленням sv. Ціна X(r) може визначатися згідно з формулою:
X(r) = Xt–1 – r(Xt–1 – Xt–2),
де Xt–1 — ціна на (t – 1)-му проміжку часу; Xt–2 — ціна на (t – 2)-му проміжку часу; r — ваговий коефіцієнт, значення котрого задається в моделі в діапазоні (0 £ r £ 1).
Якщо r = 0, то середньозважена ціна X(r) = Xt–1. Це означає, що навчання в модель не закладене. Для другого граничного випадку (r = 1) середньозважена ціна X(r) = Xt–2. Це також означає, що навчання у моделі відсутнє, але для визначення пропозиції використовується віддалене в часі значення ціни. За умови r = 0,5 середньозважена ціна X(r) дорівнює середньоарифметичному значенню цін Xt–1 та Xt–2.
До моделі треба ще долучити рівняння локальної рівноваги ринку:
St = Dt + wt,
де St — пропозиція на t-му проміжку часу; Dt — попит на t-му проміжку часу; wt — випадкова величина, котра має заданий закон розподілу.
Можна прийняти гіпотезу, що wt має нормальний закон розподілу з нульовим значенням величини математичного сподівання та із середньоквадратичним відхиленням — sw. Система рівнянь (1.1)—(1.4) після відповідних простих перетворень зводиться до такого виразу:
Xt = F(Xt–1, Xt–2),
де F(Xt–1, Xt–2) — функція, що є оцінкою кореляційно-регресійного зв’язку між змінними Xt, Xt–1, Xt–2.
Спочатку необхідно якимось наближеним способом визначити ціну для перших двох проміжків часу. Після цього можна проводити обчислення згідно з виразом (1.5) певну кількість разів (ітерацій). Результати обчислень можуть бути подані також у графічному вигляді. Задача аналізу полягає у дослідженні впливу параметрів системи на характер залежності ціни у часі (як функції часу), а також у знаходженні рівноважної ціни.
4. Класифікація економіко-математичних моделей
Для класифікації економіко-математичних моделей використовують різні класифікаційні ознаки.
За цільовим призначенням економіко-математичні моделі поділяються на теоретико-аналітичні, що використовуються під час дослідження загальних властивостей і закономірностей економічних процесів, і прикладні, що застосовуються у розв’язанні конкретних економічних задач (моделі економічного аналізу, прогнозування, управління).
Відповідно до загальної класифікації математичних моделей вони поділяються на функціональні та структурні, а також проміжні форми (структурно-функціональні). Типовими структурними моделями є моделі міжгалузевих зв’язків. Прикладом функціональної моделі може слугувати модель поведінки споживачів в умовах товарно-грошових відносин.
Моделі поділяють на дескриптивні та нормативні. Прикладом дескриптивних моделей є виробничі функції та функції купівельного попиту, побудовані на підставі опрацювання статистичних даних. Типовим прикладом нормативних моделей є моделі оптимального (раціонального) планування, що формалізують у той чи інший спосіб цілі економічного розвитку, можливості і засоби їх досягнення.
За характером відображення причинно-наслідкових аспектів розрізняють моделі жорстко детерміновані і моделі, що враховують випадковість і невизначеність.
За способами відображення чинника часу економіко-математичні моделі поділяються на статичні й динамічні.
Моделі економічних процесів надзвичайно різноманітні за формою математичних залежностей. Важливо виокремити клас лінійних моделей, що набули значного поширення завдяки зручності їх використання. Відмінності між лінійними і нелінійними моделями є суттєвими не лише з математичного погляду, а й у теоретико-економічному плані, адже багато залежностей в економіці мають принципово нелінійний характер.
За співвідношенням екзогенних і ендогенних змінних, які включаються в модель, вони поділяються на відкриті і закриті. Повністю відкритих моделей не існує; модель повинна містити хоча б одну ендогенну змінну. Повністю закриті економіко-математичні моделі, тобто такі, що не містять екзогенних змінних, надзвичайно рідкісні. Переважна більшість економіко-математичних моделей посідає проміжну позицію і розрізняється за ступенем відкритості (закритості).
Класифікація видів математичних моделей може проводитися й за такими ознаками: аналітичне та комп’ютерне моделювання (рис.3.4).
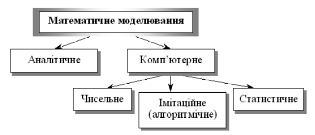
Рис 3.4. Аналітичне та комп’ютерне моделювання
Для аналітичного моделювання характерним є те, що процеси функціонування елементів системи записують у вигляді деяких математичних співвідношень (алгебраїчних, інтегро-диференційних, кінцево-різницевих тощо) чи логічних умов.
Комп’ютерне моделювання характеризується тим, що математична модель системи (використовуючи основні співвідношення аналітичного моделювання) подається у вигляді деякого алгоритму та програми, придатної для її реалізації на комп’ютері, що дає змогу проводити з нею обчислювальні експерименти. Залежно від математичного інструментарію (апарату), що використовується в побудові моделі, та способу організації обчислювальних експериментів можна виокремити три взаємопов’язані види моделювання: чисельне, алгоритмічне (імітаційне) та статистичне.
У чисельному моделюванні для побудови комп’ютерної моделі використовуються методи обчислювальної математики, а обчислювальний експеримент полягає в чисельному розв’язанні деяких математичних рівнянь за заданих значень параметрів і початкових умов.
Алгоритмічне (імітаційне) моделювання (може бути детермінованим та стохастичним) — це вид комп’ютерного моделювання, для якого характерним є відтворення на комп’ютері (імітація) процесу функціонування досліджуваної складної системи.
Статистичне моделювання — це вид комп’ютерного моделювання, який дозволяє отримати статистичні дані відносно процесів у модельованій системі.
5. Основні дефініції економіко-математичного моделювання
Якщо йдеться про математичну модель, що описує механізм функціонування певної гіпотетичної економічної чи соціально-економічної системи, то таку модель називають економіко-математичною чи просто економічною. Під економіко-математичною моделлю розуміють концентроване вираження найсуттєвіших економічних взаємозв’язків досліджуваних об’єктів (процесів) у вигляді математичних функцій, нерівностей і рівнянь.
Математична модель — це об’єкт, котрий створюється системним аналітиком для отримання нових знань про об’єкт-оригінал і відбиває лише суттєві (з погляду системного аналітика) властивості об’єкта-оригіналу.
Модель вважається адекватною об’єкту-оригіналу, якщо вона з достатнім ступенем наближення, на рівні розуміння системним аналітиком модельованого процесу відбиває закономірності процесу функціонування реальної економічної системи у зовнішньому середовищі.
Як було зазначено, під моделюванням розуміють процес побудови, вивчення й використання моделей.
Процес моделювання включає три системотвірних елементи:
· суб’єкт дослідження (системний аналітик);
· об’єкт дослідження;
· модель, яка опосередковує відносини між об’єктом, який вивчається, та суб’єктом, який пізнає (системним аналітиком).
У загальних рисах можна виокремити чотири основні етапи процесу математичного моделювання економічних систем і подати їх за такою узагальненою схемою (рис. 3.5).
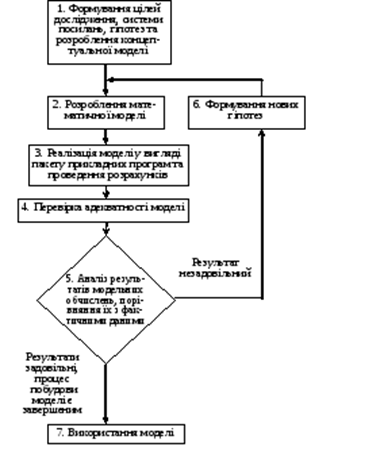
Рис. 3.5. Узагальнена схема процесу економіко-математичного моделювання
Головним гальмом для практичного застосування математичного моделювання в економіці є проблема наповнення розроблених моделей конкретною та якісною інформацією. Точність і повнота первинної інформації, реальні можливості її збору й опрацювання справляють визначальний вплив на вибір типів прикладних моделей. З іншого боку, завдання моделювання економіки висувають нові вимоги до системи інформації.
Залежно від модельованих об’єктів і призначення моделей використовувана в них вхідна інформація має суттєво відмінний характер і походження. Вона може бути розподіленою на дві категорії: щодо минулого розвитку та сучасного стану об’єктів (економічне спостереження й опрацювання); про майбутній розвиток об’єктів, яка включає дані про очікувані зміни, внутрішні параметри та зовнішні умови (прогнози). Інша категорія інформації є результатом самостійних досліджень, які також можуть проводитися за допомогою моделювання.
Методи економічних спостережень і використання їхніх результатів розробляються економічною статистикою. З огляду на це варто визначити лише специфічні проблеми економічних спостережень, які стосуються моделювання економічних процесів. В економіці чимало процесів є масовими: вони характеризуються закономірностями, що не проявляються на підставі лише одного чи кількох спостережень. Тому моделювання в економіці має спиратися на масові спостереження.
Інша проблема породжується динамічністю економічних процесів, мінливістю їхніх параметрів і структурних відношень. Унаслідок цього доводиться постійно вивчати економічні процеси, здійснювати їх моніторинг. Оскільки спостереження за цими процесами й опрацювання емпіричних даних зазвичай забирають досить багато часу, то, будуючи економіко-математичні моделі, необхідно коригувати вхідну інформацію з урахуванням її надходження із деяким запізненням у часі.
Дослідження кількісних відношень економічних процесів і явищ спирається на економічні виміри. Точність проведення вимірювань значною мірою впливає на точність кінцевих результатів кількісного аналізу. Тому застосування математичного моделювання загострило проблему вимірювання та кількісного зіставлення різних аспектів і явищ соціально-економічного розвитку та повноти одержуваних даних, захисту їх від навмисних і технічних викривлень (деформації).
6. Етапи економіко-математичного моделювання
В різних галузях знань, зокрема в економіці, етапи моделювання набувають специфічних рис. Проаналізуймо послідовність і зміст етапів одного циклу економіко-математичного моделювання.
1. Постановка економічної проблеми та розроблення концептуальної моделі. Головне на цьому етапі — чітко сформулювати сутність проблеми (цілі дослідження), припущення, що приймаються, і ті питання, на які необхідно одержати відповіді. З урахуванням цілей дослідження проводиться якісний аналіз об’єкта; виокремлюються, абстрагуючись від другорядних, найважливіші риси і властивості об’єкта, що моделюється. З позиції системного підходу вивчаються структура об’єкта й головні взаємозв’язки між його елементами (підсистемами). Обираються та обґрунтовуються основні показники й система гіпотез, що пояснюють поведінку та розвиток об’єкта і на основі яких буде відбуватись подальша формалізація.
На цьому етапі моделювання широко застосовуються якісні методи описання систем, знакові та мовні моделі. Таке попереднє, наближене зображення системи називають концептуальною моделлю.
2. Розроблення математичних моделей. Це етап формалізації економічної проблеми, вираження її у вигляді конкретних математичних залежностей і відношень (функцій, рівнянь, нерівностей тощо). На цьому етапі проводиться теоретичне (аналітичне) дослідження моделі, обираються методи дослідження й розв’язку.
Метою теоретичного (аналітичного) дослідження є з’ясування загальних властивостей моделі. Найважливіший момент — доведення існування розв’язку для моделі. Знання загальних властивостей моделі настільки важливе, що часто задля доведення подібних властивостей дослідники свідомо йдуть на ідеалізацію первинної моделі. У тому разі, коли аналітичними методами не вдається з’ясувати загальні властивості моделі, а спрощення моделі спричиняється до недопустимих (неадекватних) результатів, переходять до числових методів дослідження.
3. Реалізація моделі у вигляді пакету прикладних програм (ППП) та проведення розрахунків. Цей етап включає розробку алгоритмів для числового розв’язування задачі, складання програм на ЕОМ (можливе використання існуючих ППП з відповідною адаптацією) і безпосереднє проведення розрахунків. Труднощі цього етапу зумовлені передусім великою розмірністю економічних задач, необхідністю опрацювання значних масивів інформації. Завдяки високій швидкодії сучасних ЕОМ вдається проводити числові «модельні» експерименти, вивчаючи «поведінку» моделі за різних значень деяких умов. Дослідження, що проводяться за допомогою числових методів, можуть стати суттєвим доповненням до результатів аналітичного дослідження. Клас економічних задач, які можна розв’язувати числовими методами, значно ширший, ніж клас задач, доступних аналітичному дослідженню.
4. Перевірка адекватності моделі. Вимога адекватності є суперечною вимозі простоти, і це слід враховувати, перевіряючи модель на адекватність. Початковий варіант моделі попередньо перевіряється за такими основними аспектами: чи всі суттєві параметри включені в модель; чи містить модель несуттєві параметри; чи правильно відображені функціональні зв’язки між параметрами; чи правильно визначені обмеження на значення параметрів тощо.
Для встановлення відповідності створюваної моделі оригіналу використовують такі методи:
· порівняння результатів моделювання з окремими експериментальними результатами, одержаними за однакових (подібних) умов;
· використання інших схожих моделей;
· порівняння структури і функціонування моделі з прототипом.
Головним шляхом перевірки адекватності моделі досліджуваного об’єкта виступає практика. Але вона потребує накопичення статистики, котра не завжди буває достатньою для отримання надійних даних. Для багатьох моделей перші два методи виявляються менш прийнятними. Тоді залишається лише один шлях: висновок про подібність моделі та прототипу робити на підставі порівняння їхніх структур і виконуваних функцій. Такі висновки не мають формального характеру, оскільки ґрунтуються на досвіді та інтуїції дослідника.
Згідно з результатами перевірки моделі на адекватність приймається рішення про можливість її практичного використання чи проведення коригування.
5. Аналіз числових результатів та прийняття відповідних рішень. Результати досліджень подаються у вигляді, зручному для огляду, і на основі обробки отриманих результатів проводиться аналіз матеріалів дослідження моделі. На цьому, завершальному, етапі виникає питання про правильність і повноту результатів моделювання, про можливість практичного застосування останніх, і, найголовніше, про досягнення цілей дослідження.
Звернімо увагу на зворотні зв’язки етапів, які виникають унаслідок того, що в процесі дослідження виявляються недоліки попередніх етапів моделювання. Недоліки, які не вдається виправити на проміжних етапах моделювання, усуваються в наступних циклах. Але результати кожного циклу мають і цілком самостійне значення. Розпочавши дослідження від побудови простої моделі, можна швидко одержати корисні результати, а потім перейти до створення досконалішої моделі.
Шрифти
Розмір шрифта
Колір тексту
Колір тла
Кернінг шрифтів
Видимість картинок
Інтервал між літерами
Висота рядка
Виділити посилання
Вирівнювання тексту
Ширина абзацу