Тема 4. Виробничі функції у науковому проєктуванні
| Сайт: | Навчально-інформаційний портал НУБіП України |
| Курс: | Економетричне моделювання наукових бізнес-проєктів☑️ |
| Книга: | Тема 4. Виробничі функції у науковому проєктуванні |
| Надруковано: | Гість-користувач |
| Дата: | четвер, 5 лютого 2026, 03:30 |
1. Загальне поняття виробничої функції
Нашим завданням є виокремити з множини моделей виробничу функцію (ВФ) як особливий вид економіко-статистичних моделей.
Об’єкт моделювання. Безпосереднім об’єктом моделювання щодо виробничої функції є процеси виробництва продукції в реально функціонуючих протягом певного відрізку часу господарських системах на підприємстві (фірмі), в галузі, регіоні чи в народному господарстві загалом. Відповідно, щодо рівня модельованої системи виробничі функції поділяються на макроекономічні, регіональні, галузеві, а також виробничі функції підприємства.
У низці випадків як самостійний об’єкт моделювання розглядається не вся господарська система, а її частина, що складається з технічно відносно однорідних виробничих одиниць.
Системний опис об’єкта. У теорії виробничих функцій виробничий процес аналізується з погляду перетворення ресурсів у продукт (продукцію). Входами є потоки ресурсів різноманітного виду, повністю чи частково використовувані у виробництві, виходом — готова до реалізації продукція. Функціонуючі в системі ресурси (чинники), технологія та умови організації виробництва визначають потенційні можливості та стан процесу (системи).
Цілі моделювання. ВФ будується для розв’язання певних економічних задач, що стосуються аналізу, прогнозування й планування (у вузькому розумінні слова). Використовуються ВФ як самостійно, так і в складі більш загальних економіко-математичних моделей. Мету побудови ВФ можна охарактеризувати як аналіз чинників щодо суттєвого впливу їх на обсяги випуску продукції.
Однак у кожній конкретній ситуації ця мета має свої особливості, що істотно впливають на процес побудови функції. Доцільно розрізняти такі можливі способи використання ВФ:
· визначення обсягів випуску за фіксованих обсягів та показників основних ресурсів (випадок, коли ці обсяги несуттєво відрізняються від тих, що спостерігались у минулому);
· те саме щодо випадку обсягів ресурсів, котрі суттєво відрізняються від усіх, що спостерігалися в минулому;
· визначення обсягів випуску за заданих значень обсягів ресурсів, що належать до деякої неперервної області (зокрема таких, що змінюються в заданих межах);
· визначення впливу на обсяг випуску малої зміни обсягів одного чи кількох ресурсів;
· визначення (виявлення) характеристик виробничого процесу, що виражається через параметри ВФ.
Принципи моделювання. В основі найпоширенішого поняття ВФ лежать принципи, котрі виражають роль аксіоматичних положень теорії виробничих функцій:
· обсяг випуску продукції, виробленої даною виробничою системою за певний період, визначається обсягами засобів та предметів праці й живої праці, що беруть участь у процесі виробництва впродовж цього періоду;
· зв’язок між обсягами випуску й обсягами засобів праці, предметів праці й живої праці є для даної виробничої системи закономірним і відносно стійким;
· у низці випадків додатково береться гіпотеза, що в певних межах будь-яка незалежна зміна аргументів ВФ допускає реальну інтерпретацію.
Апарат моделювання. Основним «матеріалом» для побудови виробничої функції є залежності y = f (x1, ..., xn), де y — показник випуску (обсяг), x1, ..., xn — обсяги виробничих ресурсів (чинників) (кількість чинників ВФ, як правило, не перевищує 10). Функція f (•) вважається визначеною в досить широкій області n-мірного евклідового простору (Rn) та такою, що обчислюється в області свого визначення. Останнє означає, що системний аналітик повинен мати у своєму розпорядженні алгоритм, який дозволяв би обчислювати значення f (•) у будь-якій точці, де вона визначена. Як правило, ВФ y = f (x1, ..., xn) будується шляхом підбору найбільш адекватних функцій із певного параметричного класу F = {y = f (x1, ..., xn, a1, ..., ak)} = f (x, a), де a = (a1, ..., ak) — вектор параметрів.
Отже, безпосереднім апаратом моделювання в межах даної концепції ВФ є параметричні класи функцій, що залежать від змінних. Як правило, залежність функції f(•) від змінних і параметрів задається в явному вигляді (або режимі) чи у вигляді функціональних диференціальних чи інтегральних рівнянь.
Ідентифікація й інтерпретація моделі.
Змінні y, x1, ..., xn ототожнюються
з показниками обсягів випуску й основними, які беруть участь у виробництві,
чинниками (ресурсами). Припускається можливість специфікації параметрів a1, …, ak ВФ
на підставі статистичних (чи експертних) даних щодо ресурсів та випуску
продукції за попередні періоди, а також планових і опосередкованих даних. Метод
оцінки параметрів не визначається однозначно, він залежить від цілей побудови
ВФ, особливостей модельованого процесу та вихідних даних. Інтерпретація
параметрів, у свою чергу, залежить від методу їх оцінювання. Часто для
інтерпретації виокремлених параметрів залучаються їх вирази через значення
показників, а також значення часткових похідних 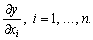
2. Економічний зміст виробничої функції
Вважається, що ВФ є економіко-статистичною моделлю процесу виробництва продукції в даній економічній системі й виражає стійку закономірну кількісну залежність між об’ємними показниками ресурсів і випуску продукції. Основним елементом процесу виробництва є, як відомо, праця як свідома цілеспрямована діяльність людини, а також предмети й засоби праці. Кількість та якість виробленої продукції визначаються обсягом та структурою цих чинників, а також способом організації їх взаємодії.
У складі предметів праці виокремлюють сировину, матеріали, напівфабрикати, комплектувальні складові — усі ті елементи, які ввійдуть у готову продукцію. Засоби праці, у свою чергу, поділяються на знаряддя праці (обладнання, машини, двигуни, інструменти, оснащення тощо), будівлі та споруди, засоби комунікації й транспорту. Неоднорідною за своїм складом є й сама праця: розрізняють окремі професійно-кваліфікаційні групи персоналу тощо.
Продукція, як правило, теж не є однорідною як за функціональними характеристиками, так і за способом виробництва. За певний період часу (наприклад за рік) дана виробнича система виробляє та реалізує споживачам продукцію широкої номенклатури.
Виробничий процес у певній ланці управління — підприємстві (фірмі) — здійснюється на основі певної технології, тобто сукупності прийомів і способів переробки сировини, матеріалів, напівфабрикатів у готову продукцію.
Реально існуючий спосіб виробництва визначається, з одного боку, прагненням до оптимального узгодження технологій, а з другого — обмеженими можливостями щодо забезпечення ресурсами та їх розміщення. По суті, обмеження в застосуванні технологій викликані двома основними причинами: неможливістю за короткий термін змінити і структури виробничих ресурсів, і умови, що їх накладає зовнішнє середовище (народногосподарські та зовнішньоекономічні вимоги).
Якщо йдеться про опис виробничого процесу протягом тривалого проміжку часу, то обмеження, що пов’язані з перетворенням ресурсів, послаблюються, і як основний чинник, що визначає випуск (поряд з якістю та кількістю ресурсів), виступають економічні обмеження.
Подібно до того, як поняття технології виробництва розширюється до поняття технології багатономенклатурного виробництва, природного сенсу набуває й поняття технології щодо більш узагальнених економічних систем — промислового об’єднання, холдингу, підгалузі, галузі, регіону. У цьому випадку кількість технологічних способів, природно, зростає. Відповідно, дедалі більшу роль відіграють організаційно-економічні аспекти, що накладають обмеження на можливості реалізації оптимальної комбінації та узгодження елементарних технологій.
У реальній виробничій діяльності економічних систем технологія є лише відносно стабільною. Постійно відбувається процес еволюційного розвитку (можливий і занепад), удосконалюються знаряддя праці, з’являються нові види матеріалів, упроваджуються досягнення науки. Разом з тим виробничі процеси загалом характеризуються певними стійкими ознаками.
Використовуючи групові характеристики ресурсів і продукції, можна вести мову про групову (агреговану) технологію — спосіб переробки різного виду сировини, матеріалів, напівфабрикатів у готову продукцію заданих функціональних груп. Така технологія описує взаємодію ресурсів уже не на рівні окремих видів обладнання, оснащення, матеріалів і працівників, а на рівні узагальнених агрегованих показників — витрат ресурсів. Побудова таких показників (окрім трудових) спирається в основному на вартісні категорії.
Технологічний розвиток підприємств (фірм), поєднаний, зокрема, зі змінами елементарних технологій, — процес безперервний. Однак чим більш агреговано розглядається економічна система, чим вищий рівень агрегування показників, тим стабільнішою є агрегована технологія. У цьому розумінні можна говорити про технологічну еволюцію як про форму динаміки економічної технології (хоча впродовж короткого часового інтервалу такий еволюційний підхід правомірно використовувати й для підприємств, фірм, галузей). Отже, наявним є економічний стрибок.
Оскільки ВФ призначена для відображення певної агрегованої економічної технології, моделювання для відповідного періоду доцільно здійснювати так, щоб ураховувався технологічний стрибок.
Питання щодо стійкості агрегованої економічної технології пов’язане не лише зі стабільністю структури й інтенсивністю застосовуваної технології, але й з незмінністю показників, що використовуються для вимірювання ресурсів і випуску продукції.
Найвищий ступінь агрегування ресурсів досягається тоді, коли всі виробничі ресурси характеризуються двома узагальнюючими чинниками, що відображають відповідно обсяги матеріалізованої (минулої) та живої праці.
3. Загальна характеристика та етапи побудови виробничих функцій
Поняття ВФ певного об’єкта як функції, що разом з областю визначення найкращим чином апроксимує агреговану економічну технологію t, визначає строгу послідовність дій для побудови ВФ.
Оскільки ВФ будується в результаті використання обчислювального методу та оптимізації V, етапом у цій побудові є використання так званих пробних функцій та областей їх визначення, тобто вибір бінарного відношення rt на множині обчислюваних функцій. Вибір цього відношення відіграє визначальну роль у побудові ВФ, оскільки в нього входить і визначення виду функції, і формування принципів оцінювання параметрів. Для цього потрібно зібрати, опрацювати й використати необхідну інформацію щодо виробничого процесу та впливу на нього зовнішніх умов, сформулювати цілі й завдання, для розв’язання яких будується ВФ, проаналізувати засади існування та властивості економіко-технологічної функції t; як правило, попередньо фіксується система показників оцінки ресурсів і випуску (m, n). Виокремлюють такі етапи побудови ВФ:
Етап 1. Формулювання цілей побудови ВФ.
Етап 2. Системний аналіз об’єкта, що моделюється.
Етап 3. Економічний якісний аналіз об’єкта.
Етап 4. Визначення системи показників виробничої функції (m, n).
Етап 5. Формування інформаційної бази для аналізу технології та для побудови ВФ.
Етап 6. Аналіз існування та властивості економічної технології.
Етап 7. Визначення принципів порівняння функцій щодо їх наближення до технології t (формування відношення) r = rt.
Етап 8. Визначення обчислювального алгоритму V для оптимізації відношення rt.
Етап 9. Підготовка (вибір) програмного забезпечення щодо реалізації алгоритму на комп’ютері.
Етап 10. Обчислення ВФ та її використання.
4. Види виробничих функцій
Нехай Фп —
множина всіх функцій від п змінних, визначених у деякій
області М простору Rn. Підмножина F I Фn називається параметричною (точніше, k-параметричною),
якщо існує під- множина Ak I Rn і
відображення r: Ak ® Фn, тобто таке, щоr(A) = F.У k-параметричному
класі F кожна функція 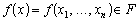
цілком визначається вектором параметрів a = (a1, ..., ak) і може бути записана як fa(x). Зміст параметризації деякої множини функцій, по суті, є аналогічним уведенню системи координат, за допомогою якої кожна функція з цієї множини ототожнюється з послідовністю своїх координат. Параметризацію допускають лише не дуже широкі множини F, зокрема, множина Фп не може бути k-параметричною за жодного скінченого k. Якщо відображення ? є лінійним, тобто p(a' + a'') = p(a') + p (a''), a', a'' I Ak, то клас F утворюють функції, лінійні за параметром. Що ж спільного можуть мати функції f, які належать деякій параметричній множині F? Припустимо, що всі функції f I F диференційовані до другого порядку включно, а множина Ak збігається з Rn.
Співвідношення
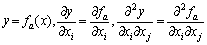 розглядатимемо
як систему з
розглядатимемо
як систему з 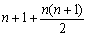 рівнянь
відносно k параметрів a1, ..., ak.
Кількість параметрівk, як правило, має той самий порядок, що й кількість
змінних
, тому
здебільшого параметри a1, ..., an можна виразити
як функції від x1, ..., xn, y,
рівнянь
відносно k параметрів a1, ..., ak.
Кількість параметрівk, як правило, має той самий порядок, що й кількість
змінних
, тому
здебільшого параметри a1, ..., an можна виразити
як функції від x1, ..., xn, y, 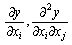 ,
використовуючи k рівнянь з цієї системи. Підставляючи отримані
вирази у рівняння, що залишилися, можна отримати систему диференційних рівнянь
щодо функції f(•), яка вже не містить параметрів. Часто у
такий спосіб вдається досягти того, щоб множина розв’язків отриманої системи
рівнянь щодо функції f(•) збіглася б з F,
тобто F був би загальним інтегралом системи. Власне, те, що
функції з класу, який задовольняє цю систему диференційних рівнянь з частковими
похідними, і є тією властивістю, що об’єднує їх. Ця обставина дає ключ до
вибору виду виробничої функції певного об’єкта. Система диференційних рівнянь
(разом із частковими похідними за чинниками є визначальною у формуванні таких
систем. Використовуються також інші характеристичні функції — середня
ефективність чинника, еластичність випуску за чинником, гранична норма
заміщення чинника тощо), що поєднує між собою в загальному випадку значення
функції, її аргументів і характеристик (в тій самій точці, що й значення
функції). Інформація, що може бути отримана на стадії якісного (вербального)
економічного аналізу модельованого об’єкта, часто дозволяє прийняти чи
відхилити припущення щодо існування такого зв’язку.
,
використовуючи k рівнянь з цієї системи. Підставляючи отримані
вирази у рівняння, що залишилися, можна отримати систему диференційних рівнянь
щодо функції f(•), яка вже не містить параметрів. Часто у
такий спосіб вдається досягти того, щоб множина розв’язків отриманої системи
рівнянь щодо функції f(•) збіглася б з F,
тобто F був би загальним інтегралом системи. Власне, те, що
функції з класу, який задовольняє цю систему диференційних рівнянь з частковими
похідними, і є тією властивістю, що об’єднує їх. Ця обставина дає ключ до
вибору виду виробничої функції певного об’єкта. Система диференційних рівнянь
(разом із частковими похідними за чинниками є визначальною у формуванні таких
систем. Використовуються також інші характеристичні функції — середня
ефективність чинника, еластичність випуску за чинником, гранична норма
заміщення чинника тощо), що поєднує між собою в загальному випадку значення
функції, її аргументів і характеристик (в тій самій точці, що й значення
функції). Інформація, що може бути отримана на стадії якісного (вербального)
економічного аналізу модельованого об’єкта, часто дозволяє прийняти чи
відхилити припущення щодо існування такого зв’язку.
Для кожного з видів функцій можна вказати одну чи кілька систем умов для характеристики функцій даного виду, що однозначно виокремлюють цей вид з-поміж інших. Ці умови являють собою чи співвідношення між різними характеристиками функції, чи опис поведінки окремих характеристик на різних підобластях області її визначення.
5. Макроекономічні виробничі функції
Як зазначалося у попередньому матеріалі, виробнича функція (ВФ) відображає залежність результату від витрат ресурсів. У формалізованому описі економіки (точніше, її виробничої підсистеми) за допомогою ВФ ця підсистема розглядається як «чорна скринька», на вхід якої постачають ресурси R1, …, Rn, а на виході отримують результати у вигляді річних обсягів виробництва різних видів продукції X1, …, Xm.
Як ресурси (чинники виробництва) на макрорівні здебільшого розглядаються накопичена (уречевлена) праця у формі виробничих фондів (капітал) K і поточна (жива) праця L. А як результат — валовий випуск X (чи валовий внутрішній продукт Y, чи національний дохід N). У всіх випадках результат узагальнено називатимемо випуском і позначатимемо через X.
Стосовно до обґрунтування чинника K можна твердити, що минула праця втілена в основних і обігових, виробничих і невиробничих фондах.
Вибір конкретної структури K визначається метою дослідження, а також структурою розвитку виробничої і невиробничої сфер упродовж досліджуваного періоду часу. Якщо в цей період у невиробничу сферу вкладається приблизно постійна частка ново- створеної вартості, і невиробнича сфера має приблизно однаковий вплив на виробництво, то це є підставою для того, щоб у ВФ враховувати лише виробничі фонди. Виробничі фонди складаються з основних і обігових. Якщо структура їх (співвідношення між цими складовими) приблизно постійна впродовж періоду, за який вивчається об’єкт дослідження, то достатньо враховувати у ВФ лише основні виробничі фонди.
Отже, економіка заміщується своєю моделлю у формі, взагалі кажучи, нелінійної ВФ:
X = F(K, L), (4.1)
тобто випуск продукції є функцією від затрат ресурсів (засобів і праці).
Далі аналізуватимемо основні характеристики ВФ на прикладі неокласичної мультиплікативної ВФ (зокрема функції Кобба—Дугласа) та деяких інших, що використовуються в економічних моделях на макроекономічному рівні.
Виробничу функцію X = F(K, L) називають неокласичною, якщо вона є гладкою і задовольняє умови, які мають чітку, несуперечливу, обґрунтовану економічну інтерпретацію:
1) F(0, L) = F(K, 0) = 0 — за відсутності одного з ресурсів виробництво не є можливим;
2)
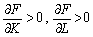 —
зі зростанням обсягів ресурсів зростає й випуск;
—
зі зростанням обсягів ресурсів зростає й випуск;
3)
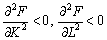 —
зі зростанням обсягів ресурсів швидкість зростання випуску знижується;
—
зі зростанням обсягів ресурсів швидкість зростання випуску знижується;
4) F(+?, L) = F(K, +?) = ? — за необмеженого зростання обсягів одного з ресурсів випуск також необмежено зростає.
Мультиплікативна ВФ задається виразом:
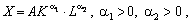 (4.2)
(4.2)
де А — коефіцієнт нейтрального технічного прогресу; ?1, ?2 — коефіцієнти еластичності за фондами K і працею L відповідно. Отже, ВФ (4.2) має властивість 1, що є адекватним реальній економіці: за відсутності одного з ресурсів виробництво неможливе.
Частковим випадком
неокласичної мультиплікативної ВФ є функція Кобба—Дугласа: 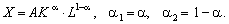
Мультиплікативна
ВФ визначається за даними часового ряду випуску і витрат ресурсів (Xt, Kt, Lt), t = 1,
…, T, де Т — довжина часового ряду, і вважається,
що має місце Т співвідношень: 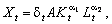
де dt — коригуючий випадковий коефіцієнт, який приводить у відповідність фактичний і теоретичний випуски і відображає флуктуацію результатів під впливом низки інших (випадкових) чинників, окрім цього, математичне сподівання Md = md = 1.
Оскільки в
логарифмах ця функція є лінійною: 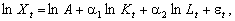
де et = lndt, Me = me = 0, то отримуємо модель лінійної множинної регресії. Параметри функції: А, a1, a2 можуть бути визначені з використанням методу найменших квадратів за допомогою низки стандартних пакетів прикладних програм, які реалізують метод множинної регресії (приміром, STATGRAF чи SAS для персональних ЕОМ).
Як приклад можна навести мультиплікативну функцію валового випуску продукції однієї з країн, яка обчислюється на підставі статистичних даних за декілька років і систематично оновлюється на основі використання нових даних за поточний період. Зокрема, виходячи з даних за 1960—1994 рр. можна подати виробничу функцію (валовий випуск) Російської Федерації (млрд руб.) залежно від вартості основних виробничих фондів (млрд руб.) і чисельності зайнятих у народному господарстві (млн осіб) (усі вартісні показники наведено у порівнянних цінах для даного періоду):
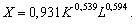 (4.3)
(4.3)
Мультиплікативна функція задовольняє також властивість 2, що є адекватним реальній економіці: зі зростанням витрат ресурсів випуск також зростає, тобто:
оскільки 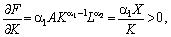 (4.4)
(4.4)
Частинні похідні випуску за чинниками, що їх називають граничними продуктами, або граничними (маржинальними) ефективностями чинників, є приростом випуску на малу частку приросту чинника:
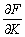 —
граничний продукт засобів (гранична капіталовіддача, гранична ефективність засобів);
—
граничний продукт засобів (гранична капіталовіддача, гранична ефективність засобів);
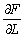 —
граничний продукт праці (гранична продуктивність праці, гранична ефективність
праці).
—
граничний продукт праці (гранична продуктивність праці, гранична ефективність
праці).
Для
мультиплікативної функції з (4.4) випливає, що гранична капіталовіддача пропорційна
середній капіталовіддачі 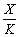 з
коефіцієнтом a1, а гранична продуктивність праці — середній продуктивності
праці
з
коефіцієнтом a1, а гранична продуктивність праці — середній продуктивності
праці 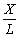 з
коефіцієнтом пропорційності a2:
з
коефіцієнтом пропорційності a2:
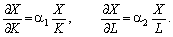 (4.5)
(4.5)
Із рівнянь (4.5)
випливає, що за a1 < 1, a2 < 1 граничні віддачі
чинників є меншими від середніх; за цих умов мультиплікативна функція має
властивість 3, що часто спостерігається у реальній економіці: зі зростанням
витрат ресурсу його гранична віддача спадає, тобто: 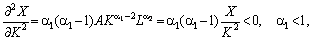
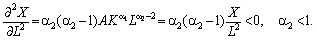 (4.6)
(4.6)
Із (4.2) також зрозуміло, що мультиплікативна функція має властивість 4, тобто за необмеженого зростання обсягу одного з ресурсів випуск також необмежено зростає. Таким чином, мультиплікативна функція 0 < a1 < 1, 0 < a2 < 1 є неокласичною.
Здійснимо економічну інтерпретацію параметрів А, ?1, ?2 мультиплікативної ВФ.
Параметр А здебільшого інтерпретують як параметр нейтрального технічного прогресу: за тих самих значень ?1 і ?2 випуск у точці (K, L) буде тим більшим, чим більше А.
Для інтерпретації параметрів ?1 і ?2 скористаємось поняттям коефіцієнтів еластичності. Існує поняття еластичностей як логарифмічних виробничих чинників:
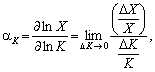 (4.6)
(4.6)
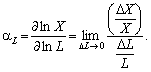
Оскільки у нашому
випадку 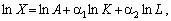
то 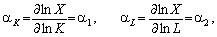
тобто ?1 — коефіцієнт еластичності випуску за основними засобами, а ?2 — коефіцієнт еластичності випуску за працею.
Із (4.6) видно, що коефіцієнт еластичності чинника показує, на скільки відсотків збільшиться випуск, якщо чинник зросте на 1 %.
Наприклад, згідно з ВФ (4.3) збільшення основних засобів (ОФ) на 1 % приведе до зростання валового випуску на 0,539 %, а збільшення зайнятих на 1 % — на 0,594 %. Якщо ?1 > ?2, то має місце працеощадне (інтенсивне) зростання.
Розгляньмо темпи зростання випуску:
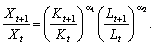 (4.7)
(4.7)
Якщо піднести
обидві частини (4.7) до ступеня 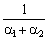 , то
отримаємо співвідношення
, то
отримаємо співвідношення
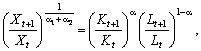 (4.8)
(4.8)
у якому праворуч
— зважене середньогеометричне темпів зростання витрат ресурсів, де ваговими
коефіцієнтами слугують відносні коефіцієнти еластичності чинників: 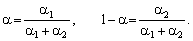
Якщо
?1 + ?2 > 1, то випуск зростає швидше, ніж у середньому
зростають чинники, а якщо ?1 + ?2 < 1 — повільніше.
Справді, якщо чинники (їх обсяги) зростають, тобто Kt+1 > Kt, Lt+1 > Lt,
то згідно з (4.7) зростає і випуск (тобто Xt+1 > Xt),
отже, за ?1 + ?2 > 1: 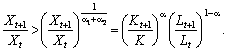
Темпи зростання випуску є більшими ніж середні темпи зростання чинників. Отже, якщо ?1 + ?2 > 1, то ВФ описує зростаючу економіку.
Лінією рівня на площині K, L, чи ізоквантою, називають множину тих точок площини, для котрих F(K, L) = X0 = const.
Для
мультиплікативної ВФ ізокванта має вигляд: 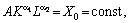
або 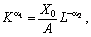
тобто це є степенева гіпербола, асимптотами якої є осі координат.
Для різних обсягів K, L, що лежать на конкретній ізокванті, випуск дорівнює значенню X0, що є еквівалентним твердженню про взаємозаміщення ресурсів. Оскільки на ізокванті F(K, L) = = X0 = const, то
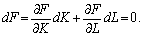 (5.18)
(5.18)
У цьому
співвідношенні
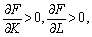 тому dK і dL мусять
мати різні знаки: якщо dL < 0, що означає скорочення
обсягів праці, то dK > 0, тобто зменшення в
обсязі
тому dK і dL мусять
мати різні знаки: якщо dL < 0, що означає скорочення
обсягів праці, то dK > 0, тобто зменшення в
обсязі
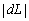 ,
праця заміщується фондами в обсязі dK.
,
праця заміщується фондами в обсязі dK.
Слушним є таке
означення, що випливає з (4.9). Граничною нормою заміщення (заміни) праці
засобами SK називають відношення модулів диференціалів ОФ і праці: 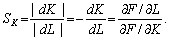
І, відповідно, гранична норма заміщення фондів працею (SL):
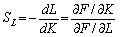 .
.
Легко помітити, що SK • SL = 1.
Для
мультиплікативної виробничої функції норма заміщення праці засобами пропорційна
капіталоозброєності: 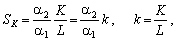
що є природним, адже брак обсягів праці можна компенсувати її кращою капіталоозброєністю.
Ізокліналями називають лінії
найшвидшого зростання ВФ. Ізокліналі ортогональні лініям нульового зростання,
тобто ортогональні ізоквантам. Оскільки напрямок найшвидшого зростання у кожній
точці (K, L) задається градієнтом 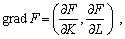
то рівняння
ізокліналі можна записати таким чином: 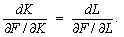
Зокрема, для
мультиплікативної ВФ маємо: 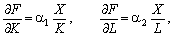
тому ізокліналь
можна задати диференціальним рівнянням: 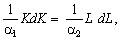
котре має
розв’язок 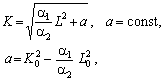
де K0, L0 — координати точки, через яку проходить ізокліналь.
Якщо припустити,
що a = 0, то отримаємо рівняння ізокліналі, що проходить
через відповідні точки площини (вона є прямою лінією): 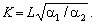
На рис. 4.1 зображені ізокванти та ізокліналі мультиплікативної ВФ.
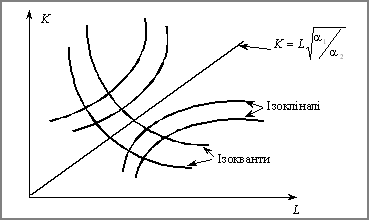
Рис. 4.1. Ізокванти та ізокліналі мультиплікативної ВФ
Аналізуючи чинники зростання економіки, виокремлюють екстенсивний чинник зростання (за рахунок збільшення обсягів витрат ресурсів, тобто збільшення масштабу виробництва) та інтенсивний чинник зростання (завдяки підвищенню ефективності використання ресурсів).
Як за допомогою ВФ вирізнити та описати масштаб та ефективність виробництва?
Це можна здійснити, якщо випуск і витрати будуть виражені у співвимірних одиницях, наприклад у вартісній формі. Найпростіше перейти до відносних (безрозмірних) показників вимірювання. У даному випадку ВФ можна подати так:
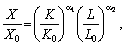 (4.10)
(4.10)
де X0, K0, L0 — значення обсягів випуску і витрат фондів і праці в базовому році.
Безрозмірну форму
(4.10) треба просто привести до початкового вигляду: 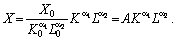
Отже,
коефіцієнт A отримує економічно прозорий зміст: 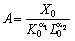
,
який зіставляє
ресурси з випуском. Якщо позначити випуск і ресурси у відносних (безрозмірних)
одиницях вимірювання через 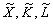 , то
ВФ у формі (5.20) можна подати таким виразом (через
):
, то
ВФ у формі (5.20) можна подати таким виразом (через
):
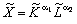 , (4.11)
, (4.11)
де 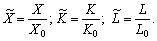
Відшукаємо тепер аналітичний вираз стосовно до ефективності економіки, скориставшись виразом (4.11).
Нагадаймо, що
ефективність — це відношення результату до витрат. У нашому випадку — два види
витрат: витрати минулої праці у вигляді засобів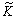 і
живої праці
і
живої праці 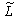 .
Отже, маємо два часткових показники ефективності:
.
Отже, маємо два часткових показники ефективності:
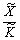 —
капіталовіддача,
—
капіталовіддача,
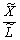 —
продуктивність праці.
—
продуктивність праці.
Оскільки часткові показники мають однакову розмірність (вони безрозмірні), то можна знаходити будь-які середні з них. Оскільки ВФ виражена в мультиплікативній формі, то і середнє природно взяти у такій самій формі, тобто як зважене середньогеометричне часткових показників ефективності:
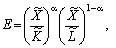 (4.12)
(4.12)
роль вагових
коефіцієнтів тут відіграють відносні еластичності: 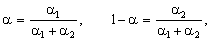
тобто часткові ефективності входять до загальної (узагальненої) ефективності з такими самими пріоритетами, з якими входять у ВФ відповідні ресурси.
Із (4.12) випливає, що за допомогою коефіцієнта економічної ефективності ВФ можна подати у формі, яка зовнішньо збігається з функцією Кобба—Дугласа:
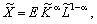 (4.13)
(4.13)
але у співвідношенні (4.13) E — не постійний коефіцієнт, а функція від (K, L).
Оскільки масштаб виробництва М подається в обсягах витрачених ресурсів, то, враховуючи ті самі міркування, що й у випадку побудови узагальненого показника економічної ефективності, визначимо і зважене середньогеометричне використаних ресурсів (як масштаб виробництва):
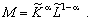 (4.14)
(4.14)
Із (4.13) і (4.14)
отримаємо, що випуск
є
добутком економічної ефективності та масштабу виробництва: 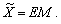 (4.15)
(4.15)
Приклад
Розгляньмо знайдену за даними 1960—1995 рр. виробничу функцію валового
внутрішнього продукту США: 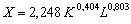
.
Обчислимо масштаб та ефективність виробництва.
Валовий внутрішній продукт США, що вимірюється в млрд дол. у цінах 1987 р., зріс з 1960 до 1995 р. у 2,82 рази, тобто ; основні виробничі фонди за цей самий період збільшились у 2,88 раза ( ), а чисельність зайнятих — у 1,93 рази ( ).
Розв’язання. Обчислимо відносні еластичності за фондами і працею:
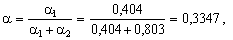 1 – a
= 0,6653.
1 – a
= 0,6653.
Визначимо тепер часткові ефективності ресурсів:
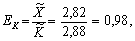
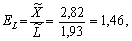
а також знайдемо
узагальнений показник ефективності як зважене середньогеометричне часткових
показників: 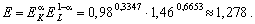
Масштаб
обчислюємо як зважене середньогеометричне темпів зростання ресурсів: 
Отже, загальне зростання ВВП з 1960 до 1995 р. у 2,82 рази стало можливим завдяки зростанню масштабу виробництва у 2,307 рази і підвищенню ефективності виробництва у 1,278 рази (2,82 = 1,273 ? 2,207).
Виробничу функцію називають однорідною степеня g, якщо:
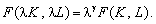 (4.16)
(4.16)
Мультиплікативна функція є однорідною степеня a1 + a2.
Що ж до
однорідних ВФ, то можна отримати спрощений вираз для норми заміщення. Дійсно, 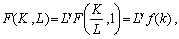
де
 —
капіталоозброєність. Тому
—
капіталоозброєність. Тому 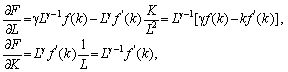
звідси маємо:
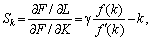 (4.17)
(4.17)
тобто норма заміщення є функцією лише капіталоозброєності.
Для однорідних ВФ уводять поняття еластичність заміни праці капіталом bK:
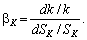 (4.18)
(4.18)
Ця величина показує, на скільки відсотків необхідно змінити капіталоозброєність, щоб досягти зміни норми заміщення на один відсоток. Аналогічно вводиться і показник еластичності заміни засобів працею bL.
Легко перевірити, що bK = bL = b.
Для
мультиплікативних ВФ b = 1. Справді, у цьому випадку 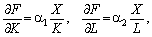
тому 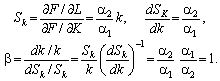
Клас ВФ з
постійною еластичністю заміни (CES-функцій) будується, зокрема, таким чином: 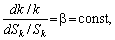
звідси
маємо:
(знаходиться
інтегруванням). Тут С — довільна константа. Підставляючи
останній вираз у (5.27), дістанемо: 
або 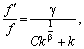
звідси 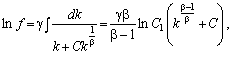
де С1 — довільна константа.
У результаті
дістаємо: 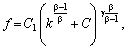
або у змінних K, L
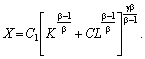
Якщо ввести
позначення: 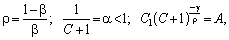
то дістанемо загальний вигляд функції з постійною еластичністю заміщення (CES-функцію).
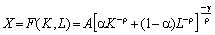 . (4.19)
. (4.19)
У цій функції A > 0, оскільки X — це випуск, а якщо 0 < g ? 1, r > –1, то вона задовольняє умови 2 і 3 для неокласичних ВФ. Якщо g = 1, b ® 1 (r ® 0), то CES-функція прямує до функції Кобба—Дугласа, а коли b ® 0 — до функції з фіксованими пропорціями X = min(Kg, Lg), котра описує випадок заміни (заміщення) чинників (b = 0). Якщо (r ® –1, g = 1, то CES-функція переходить у лінійну функцію вигляду X = EKK + ELL, де EK = Aa = = A(1 – a).
6. Двофакторні виробничі функції
У наведеному нижче списку функцій вони розташовуються в порядку зростаючої складності їх у запису й, відповідно, збільшення кількості необхідних для цього параметрів. Усі ці функції допускають можливість їх модифікації:
· Функція з фіксованими пропорціями чинників (функція Леонтьєва).
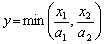 , (4.20)
, (4.20)
де а1, а2 — параметри.
Відомо кілька альтернативних систем (гіпотез), що виокремлюють функції цього виду:
а) гранична
продуктивність першого чинника є дворівневою кусково-постійною незростаючою
функцією від співвідношення
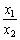 з
нульовим нижнім рівнем. Гранична продуктивність другого чинника — неспадна
кусково-постійна функція від
з
нульовим нижнім рівнем. Гранична продуктивність другого чинника — неспадна
кусково-постійна функція від 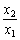 з
нульовим нижнім рівнем;
з
нульовим нижнім рівнем;
б) функція є
розв’язком такої задачі математичного програмування: 
де у — змінна, яку оптимізують;
в) функція є однорідною, а еластичність заміни чинників дорівнює нулю;
г) функція
може бути отримана з функції з постійною еластичністю виду 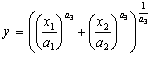
шляхом граничного
переходу: 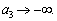
Функція Леонтьєва призначена в основному для моделювання строго детермінованих технологій, які не допускають відхилення від технологічних норм і нормативів щодо використання ресурсів на одиницю продукції. Як правило, вона використовується для формалізованого опису дрібномасштабних або цілком автоматизованих об’єктів.
· Функція Кобба—Дугласа
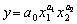 . (4.21)
. (4.21)
Тут також використовується кілька систем гіпотез, що виокремлюють клас функцій Кобба—Дугласа серед двічі диференційованих функцій від двох змінних:
а) еластичності випуску за чинниками є постійними:
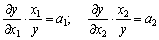
Розв’язок цієї системи диференційних рівнянь у частинних похідних першого порядку належить до класу функцій Кобба—Дугласа;
б) еластичність функції за одним із чинників є постійною, і функція є однорідною;
в) функція є однорідною, а еластичності зменшення чинників за Алленом та Михайловським дорівнюють одиниці;
г) гранична продуктивність кожного чинника є пропорційною його середній продуктивності;
д) функція є однорідною як функція від х1, х2 і як функція від х1 за будь-якого фіксованого х2;
є) функція
може бути отримана з функції з постійною еластичністю шляхом здійснення заміни
виду 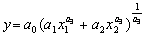
та граничного переходу а3 ® 0. Функція Кобба—Дугласа найчастіше використовується для формалізованого опису середньомасштабних господарських об’єктів та економіки країни.
· Лінійна функція
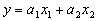 . (4.22)
. (4.22)
Передумови та гіпотези:
а) граничні продуктивності чинників є постійними:
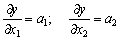 ,
,
а в нулі функція набуває нульового значення;
б) гранична продуктивність одного з чинників є постійною, і функція однорідна першого ступеня:
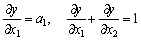 ;
;
в) функція однорідна, й еластичність заміни чинників, за Алленом, є нескінченною;
г) еластичність випуску за чинниками обернено пропорційна їхній середній продуктивності.
Лінійна функція застосовується для моделювання великомасштабних систем (велика галузь, народне господарство в цілому), у яких випуск продукції є результатом одночасного функціонування великої кількості різноманітних технологій. Особливу роль відіграє гіпотеза постійності граничних виробничих чинників чи їх необмеженого заміщення.
· Функція Аллена:
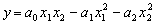 (4.23)
(4.23)
визначається за такими умовами: швидкості зростання граничних продуктивностей є постійними, і функція є однорідною.
Функція Аллена за a1, a2 > 0 призначається для формалізованого опису виробничих процесів, у яких надмірне зростання будь-якого з чинників негативно впливає на обсяг випуску продукції. Зазвичай така функція використовується для формалізованого опису дрібномасштабних виробничих систем з обмеженими можливостями переробки ресурсів.
· Функція постійної еластичності заміщення чинників (функція CES):
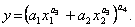 (4.24)
(4.24)
Передумови та гіпотези:
Функція є однорідною, й еластичність заміщення чинників є постійною.
Функція CES застосовується у разі відсутності точної інформації щодо рівня взаємозаміни виробничих чинників, і разом з тим є підстави вважати, що цей рівень суттєво не зміниться за зміни обсягів залучених ресурсів, тобто коли економічна технологія має властивість певної стійкості щодо певних пропорцій чинників. Функція CES (за наявності засобів оцінки її параметрів) може використовуватись для моделювання систем будь-якого рівня.
· Функція Солоу:
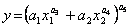 (4.25)
(4.25)
характеризується тим, що величина відсоткової зміни граничної норми заміщення чинників, що пов’язане зі зміною одного з чинників на один відсоток, не залежить від початкового рівня чинників.
Дана функція може використовуватись приблизно в тих самих ситуаціях, що й функція CES. Функція Солоу може використовуватись у моделюванні системи різних масштабів.
· Багаторежимна функція:
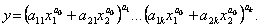 (4.26)
(4.26)
Функція є однорідною, еластичність функції за першим аргументом є згладженою k-рівневою спадною ступінчастою функцією.
Багаторежимна функція — одна з найзагальніших. Вона використовується для формалізованого опису та моделювання процесів, у яких рівень віддачі кожної додаткової одиниці ресурсу стрибкоподібно змінюється залежно від співвідношення чинників. Функцію доцільно застосовувати за наявності апріорної інформації щодо кількості режимів k, а інколи й щодо величини «перехідної» області між режимами (чим більше , тим чіткіше виокремлюються режими).
7. Багатофакторні виробничі функції
В економіко-математичному моделюванні широко використовують багатофакторні виробничі функції.
Один із найбільш раціональних способів переходу від двофакторних до багатофакторних функцій полягає в такому.
Розгляньмо двофакторну функцію:
y = j1 (x1, x2). (4.27)
Аргумент x2 цієї функції розглянемо як узагальнений показник, що залежить також від двох інших чинників x3, x4:
x2 = j2(x3, x4),
де j2 — деяка функція. Підставляючи цей вираз у формулу (4.27), отримаємо трифакторну функцію
y = j1(x1, j2(x3, x4)),
що виражає залежність показника від аргументів x1, x3, x4. Цей процес можна продовжити, вважаючи, зокрема, що х3, у свою чергу, залежить від деяких чинників.
У загальному вигляді: якщо задано (п – 1) двофакторних функцій j1(x1, x2), j2(x3, x4), jn–1(x2n–3, x2n–2), то дістанемо п-факторну функцію:
y = f(x1, ..., xn)
у результаті послідовної підстановки їх. Операція такої підстановки (суперпозиції) має очевидний економічний сенс: другий аргумент, наприклад двофакторної функції, послідовно подається у вигляді залежності від показників нижчих (деталізованих) рівнів. Неважко перевірити такі властивості операції суперпозиції:
а) якщо j1, …, jn–1 — неспадні функції, то f — також неспадна функція;
б) якщо j2, …, jn–1 — лінійно-однорідні функції, а j1 — однорідна функція ступеня однорідності g, то f — однорідна функція ступеня однорідності g;
в) якщо j1, …, jn — увігнуті неспадні функції, то f — увігнута неспадна функція.
Отже, якщо двофакторні функції j1, …, jn–1 є неокласичними, то отримана в результаті їх суперпозиції функція f також буде неокласичною.
Для виробничих функцій від n змінних справедливими є твердження, які показують, що клас функцій, поданих у вигляді суперпозиції будь-яких двофакторних функцій, є досить широким. Строго доводиться, зокрема, що будь-яка неперервна функція f(x1, …, xn) від n змінних (за умови n ? 4) може бути подана у вигляді суперпозиції неперервних функцій від трьох змінних. У свою чергу кожна неперервна функція від трьох змінних може бути отримана як суперпозиція функцій від двох змінних. Відомо також, що будь-яку неперервну функцію від двох змінних можна з будь-якою заданою точністю апроксимувати суперпозицією неперервних функцій від однієї змінної та функції y = x1 + x2
Шрифти
Розмір шрифта
Колір тексту
Колір тла
Кернінг шрифтів
Видимість картинок
Інтервал між літерами
Висота рядка
Виділити посилання
Вирівнювання тексту
Ширина абзацу