Тема 5. Алгоритмічні (імітаційні) і рейтингові моделі бізнес-проєктування
| Сайт: | Навчально-інформаційний портал НУБіП України |
| Курс: | Економетричне моделювання наукових бізнес-проєктів☑️ |
| Книга: | Тема 5. Алгоритмічні (імітаційні) і рейтингові моделі бізнес-проєктування |
| Надруковано: | Гість-користувач |
| Дата: | четвер, 5 лютого 2026, 03:30 |
Зміст
- 1. Основні аспекти імітаційного моделювання
- 2. Теоретичні основи методу статистичного моделювання
- 3. Послідовність створення математичних імітаційних моделей
- 4. Моделювання випадкових величин імітаційного процесу
- 5. Приклади імітаційного моделювання
- 6. Концепція рейтингового управління
- 7. Моделювання системи рейтингового управління та структура процесу обчислення рейтингу
- 8. Моделі й методи процесу обчислення рейтингу економічної системи
- 9. Презентація до лекції 5
1. Основні аспекти імітаційного моделювання
Як зазначалося в попередньому матеріалі, за однією з класифікаційних ознак математичні моделі можна класифікувати як аналітичні, імітаційні (алгоритмічні) та комбіновані.
З розвитком обчислювальної техніки і дискретного аналізу дедалі ширшого розвитку та використання набувають алгоритмічні (імітаційні) моделі. Серед основних етапів процесу імітаційного моделювання можна виокремити такі:
· аналіз характеристик і закономірностей функціонування керованого (досліджуваного) об’єкта: виокремлення на змістовному (вербальному, концептуальному) рівні системи обмежень (ресурсних, фізичних, правових, соціальних тощо), визначення показників вимірювання та оцінки результатів, формулювання цілей, гіпотез та проблем розвитку;
· конструювання імітаційної моделі: перехід від реального об’єкта до логічних схем, які імітують його поведінку, та алгоритмів (моделей), формальна постановка задач, що розв’язуються за допомогою імітаційного моделювання;
· підготовка системи даних для моделі: формування інформаційного забезпечення, необхідного для функціонування імітаційної моделі, зокрема, визначення структури та способів подання даних, джерел їх отримання, форм і режимів зберігання, встановлення взаємозв’язків і взаємозалежності між різними масивами та базами даних;
· програмна реалізація імітаційної моделі: створення чи адекватне використання існуючих програмних продуктів, що забезпечують можливість безпосередньої практичної реалізації моделі на персональних комп’ютерах;
· оцінка адекватності моделі: порівняння результатів, накопичених у процесі дослідної експлуатації моделі, на підставі інформації, отриманої про реальний об’єкт, який імітується, виявлення та аналіз розбіжностей і в разі необхідності внесення корекцій до моделі;
· проведення імітаційних експериментів. Очевидно, що даний етап є цільовим (власне кажучи, заради нього й будується імітаційна модель). Він включає в себе стратегічне та тактичне планування експериментів, власне експериментування («імітаційні експерименти»), котре завершується інтерпретацією отриманих результатів і прийняттям на підставі зроблених висновків рішень щодо оцінювання та управління об’єктом (підприємством, банком, фінансовою фірмою, торговельною організацією, холдингом тощо).
Стратегічне планування імітаційного експерименту спрямоване на розв’язання низки питань якісного характеру. До таких, наприклад, можна віднести формулювання гіпотез щодо характеру залежностей між параметрами моделі чи вибір конкретних методів дослідження з урахуванням їх взаємовпливу.
Тактичне планування експерименту повинно прояснити питання стосовно визначення способів та умов його проведення. Типовими задачами тактичного планування є вибір початкових значень для параметрів моделі чи визначення послідовності варіації цих значень.
Одним із важливих аспектів у процесі роботи (дослідження) з імітаційною моделлю є аналіз її чутливості. Під ним розуміють визначення ступеня мінливості значень цільових показників моделі, зумовлених мінливістю (невизначеністю, варіабельністю) вихідних параметрів. Так, якщо за відносно невеликих змін вихідних даних відбувається суттєва зміна в результатах моделювання, то це є достатньою підставою для додаткових, більш детальних досліджень, зокрема, щодо взаємозв’язків між відповідними змінними.
До позитивних якостей імітаційного моделювання можна віднести:
· надання дослідникові (системному аналітику) можливості спостереження як кінцевого результату стосовно до показників аналізованого об’єкта, так і процесу його функціонування, що дає змогу одержати шуканий результат;
· широкі можливості щодо масштабування в процесі функціонування модельованого об’єкта;
· забезпечення багатоваріантності досліджень;
· багатофункціональність імітаційних моделей, що відображається в можливостях гнучкого вибору та наступних модифікаціях системи цілей і критеріїв, які бажано розглянути під час проведення імітаційних експериментів;
Звернімо увагу також на недоліки, що притаманні імітаційним моделям:
· оскільки імітаційні моделі за своєю природою є лише засобом для проведення деякого числового експерименту, то результати, отримані за їх допомогою, являють собою не що інше, як поодинокі випадки (можливі варіанти) розвитку модельованого об’єкта. Отже, всі висновки та твердження, зроблені на їх підставі, мають евристичний характер і в певних випадках можуть суттєво викривляти дійсний стан речей;
· у багатьох випадках отримання оцінок стосовно до ступеня наближення (чи невідповідності) між імітаційною моделлю (результатами імітаційного моделювання) і функціонуванням реального об’єкта виявляються проблематичними;
· здебільшого в основу процесу імітації покладено деякий статистичний експеримент, у ході якого використовуються генератори псевдовипадкових величин. Похибки, що об’єктивно притаманні таким генераторам, можуть істотно викривляти результати, отримані в ході імітаційного моделювання.
Варто також звернути увагу на пізнавальний зворотний вплив, що його дають результати, одержані в межах імітаційних експериментів, на отримання інформації, яку використовують теоретичні (аналітичні) економіко-математичні моделі. Справді, аналіз та узагальнення накопичених у процесі імітаційних експериментів даних досить часто дозволяє краще зрозуміти якісні та кількісні закономірності, притаманні поводженню керованих об’єктів, і відобразити їх в аналітичному вигляді. Це додатково вказує на справедливість того, що успішне розв’язання задач моделювання та управління функціонуванням таких складних слабоформалізованих систем, як економічні об’єкти і процеси, потребує комплексного використання цілісної системи моделей і методів як тео- ретико-аналітичної, так і емпіричної (імітаційної) природи. Нагадаймо, що імітаційні моделі широко використовують аналітичні моделі як органічні складові, котрі є основою, на якій ґрунтуються концептуальні співвідношення, характеристики в структурі будь-якої більш-менш складної імітаційної моделі.
Імітаційні (алгоритмічні) моделі можуть бути детермінованими і стохастичними. В останньому випадку за допомогою датчиків (генераторів) випадкових чисел імітується вплив (дія) невизначених і випадкових чинників. Такий метод імітаційного моделювання дістав назву методу статистичного моделювання (статистичних прогонів, чи методу Монте-Карло). На даний час цей метод вважають одним із найефективніших методів дослідження складних систем, а часто і єдиним практично доступним методом отримання нової інформації щодо поведінки гіпотетичної системи (на етапі її проектування).
2. Теоретичні основи методу статистичного моделювання
Метод статистичного моделювання (чи метод Монте-Карло) — це спосіб дослідження невизначених (стохастичних) економічних об’єктів і процесів, коли не повністю (до певної міри) відомими є внутрішні взаємодії в цих системах.
Цей метод полягає у модельному відтворенні процесу за допомогою стохастичної математичної моделі та обчисленні характеристик цього процесу. Одне таке відтворення можливого (випадкового) стану функціонування модельованої системи називають реалізацією (чи імітаційним прогоном; далі — прогоном).
Після кожного прогону реєструють сукупність параметрів, що характеризують випадкову подію (її реалізацію). Метод ґрунтується на багатократних прогонах (випадкових реалізаціях) на підставі побудованої моделі з подальшим статистичним опрацюванням отриманих даних з метою визначення числових характеристик досліджуваного об’єкта (процесу) у вигляді статистичних оцінок його параметрів. Процес моделювання економічної системи зводиться до машинної імітації досліджуваного процесу, котрий моделюється на ЕОМ з усіма суттєвими невизначеностями, випадковостями і породженим ними ризиком. Імітаційне моделювання нерідко має назву симулятивного моделювання. Перші відомості про метод Монте-Карло були опубліковані в кінці 40-х рр. ХХ століття. Авторами методу є американські математики — економісти Дж. Нейман і С. Улам.
Теоретичною основою методу статистичного моделювання є закон великих чисел. У теорії ймовірностей закон великих чисел ґрунтується на доведенні низки теорем для різних умов збіжності за ймовірністю середніх значень результатів (на підставі великої кількості спостережень) до деяких величин.
Під законом великих чисел розуміють кілька теорем. Наприклад, одна з теорем П. Л. Чебишева формулюється таким чином: «За необмеженого збільшення кількості незалежних випробувань (n) середнє арифметичне вільних від систематичних помилок і рівноточних результатів спостережень xi випадкової величини x, яка має скінченну дисперсію D(x), збігається за ймовірністю до математичного сподівання mx = M(x) цієї випадкової величини».
Це можна записати так:
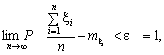 (5.1)
(5.1)
де e — як завгодно мале додатне число.
Теорема
Бернуллі
формулюється так: «За необмеженого збільшення числа незалежних спроб (п)
за одних і тих самих умов відносна частота ![]() настання випадкової
події збігається за ймовірністю до р, тобто:
настання випадкової
події збігається за ймовірністю до р, тобто:
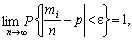 (5.2)
(5.2)
де e — як завгодно мале додатне число».
Згідно з цією
теоремою для отримання ймовірності певної події, наприклад імовірності станів
деякої системи 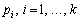 , обчислюють відносні частоти
, обчислюють відносні частоти 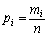 для кількості реалізацій, що дорівнює n. Результати
усереднюють і з деяким наближенням одержують шукані ймовірності станів системи.
Чим більшим буде n, тим точнішим буде результат обчислення цих
імовірностей. Це легко довести.
для кількості реалізацій, що дорівнює n. Результати
усереднюють і з деяким наближенням одержують шукані ймовірності станів системи.
Чим більшим буде n, тим точнішим буде результат обчислення цих
імовірностей. Це легко довести.
Припустимо, що треба відшукати значення математичного сподівання m для певної випадкової величини. Підберемо таку випадкову величину x, щоб
M(x) = m, а D(x) = b2 ,
де b2 — довільне значення дисперсії випадкової величини x.
Розгляньмо
послідовність n незалежних випадкових величин 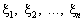 , розподіл імовірностей яких збігається з розподілом x. Якщо n
є досить великим, то згідно з центральною граничною теоремою розподіл суми
, розподіл імовірностей яких збігається з розподілом x. Якщо n
є досить великим, то згідно з центральною граничною теоремою розподіл суми 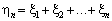
буде приблизно нормальним розподілом з параметрами a = n • m; s2 = n • b2.
З правила «трьох
сигм» 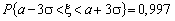 випливає, що
випливає, що
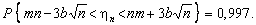 (5.3)
(5.3)
Розділивши нерівність, що розташована у фігурних дужках, на n, oтримаємо еквівалентну нерівність з тією самою ймовірністю:
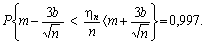
Це співвідношення можна записати у вигляді:
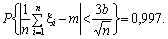 (5.4)
(5.4)
Співвідношення (5.4)
визначає метод обчислення середнього значення m і оцінку похибки. З (5.4)
видно, що середнє арифметичне реалізацій випадкової величини x наближено
дорівнюватиме числу m. З імовірністю р = 0,997 похибка такого
наближення не перевищує 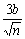 . Очевидно, що ця похибка прямує до нуля зі зростанням n,
що й потрібно було довести.
. Очевидно, що ця похибка прямує до нуля зі зростанням n,
що й потрібно було довести.
Розв’язування задач методом статистичного моделювання полягає в такому:
· опрацювання й побудова структурної схеми процесу, виявлення основних взаємозв’язків;
· формалізований опис процесу;
· моделювання випадкових явищ (випадкових подій, випадкових величин, випадкових функцій), що притаманні досліджуваній системі;
· моделювання процесу функціонування системи (на підставі використання даних, що отримані на попередньому етапі) — відтворення процесу відповідно до розробленої структурної схеми і формалізованого опису (імітаційні прогони);
· накопичення результатів моделювання (імітаційних прогонів), статистичне опрацювання, аналіз та інтерпретація їх.
Зазначимо, що будь-які твердження стосовно до характеристик модельованої системи повинні ґрунтуватися на результатах відповідних перевірок за допомогою методів математичної статистики.
Оскільки випадкові події й випадкові функції можуть подаватися з використанням випадкових величин, то й моделювання випадкових подій і випадкових функцій проводиться за допомогою випадкових величин.
Моделювання випадкових величин. Для моделювання випадкової величини потрібно знати закон її розподілу. Найзагальнішим способом отримання послідовності випадкових чисел, що є послідовністю реалізацій випадкової величини, котра розподілена за довільним законом, є спосіб, в основі якого — процес формування їх з вихідної послідовності випадкових чисел. Ця послідовність є послідовністю реалізацій випадкової величини, що розподілена в інтервалі (0; 1) згідно з рівномірним законом розподілу.
Згадану послідовність випадкових чисел з рівномірним законом розподілу можна отримати трьома способами:
· використанням таблиць випадкових чисел;
· застосуванням генераторів випадкових чисел;
· методом псевдовипадкових чисел.
Нині використовують псевдовипадкові числа, що відповідають рівномірному закону розподілу. Псевдовипадкові (випадкові) числа— це числа, отримані за деяким правилом (формулою), що імітує значення випадкової величини. Розроблено низку алгоритмів для отримання псевдовипадкових чисел. Датчики псевдовипадкових чисел є складовими більшості програмних комплексів.
Для перетворення послідовності випадкових чисел, що є реалізаціями випадкової величини з рівномірним законом розподілу в інтервалі (0; 1), у послідовність випадкових чисел, що є реалізаціями випадкової величини із заданою інтегральною функцією розподілу F(x), треба із сукупності випадкових чисел з рівномірним законом розподілу в інтервалі (0; 1) вибрати випадкове число ? і розв’язати рівняння:
F(x) = x відносно х. (5.5)
У випадку, коли задана функція щільності ймовірності f(x), співвідношення (3.5) набирає вигляду:
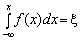 (5.6)
(5.6)
Для низки законів розподілу отримано аналітичний розв’язок рівняння (3.6), результат якого наведено в таблиці 5.1.
Таблиця 5.1
Формули для моделювання випадкових величин
|
Закони розподілу випадкової величини |
Щільність розподілу |
Формули для моделювання випадкових величин |
|
Експоненційний |
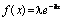 |
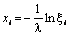 |
|
Вейбула |
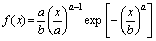 |
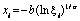 |
|
Гама-розподіл (? — цілі числа) |
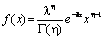 |
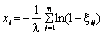 |
|
Нормальний |
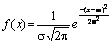 |
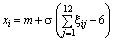 |
Моделювання випадкових подій. Моделювання випадкових подій полягає у відтворенні факту появи чи непояви випадкової події відповідно до заданої ймовірності. Моделювання повної групи несумісних подій А1, А2, …, Аn, імовірності котрих P(Ai) = pi, i = 1, …, n відомі, можна привести до моделювання дискретної випадкової величини Y, яка має закон розподілу P(yi) = pi, де ймовірність її можливих значень
P(yi) = P(Ai) = pi.
Тобто прийняття дискретною випадковою величиною Y можливого значення yі еквівалентне появі події Аі. Для практичної реалізації даного способу спочатку на одиничному відрізку числової осі відкладають інтервали Di = pi.
Генерують рівномірно розподілену на інтервалі (0; 1) випадкову величину, реалізацією котрої є випадкове число xj, і перевіряють умову:
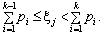 (5.7)
(5.7)
При виконанні умови (5.7) вважають, що за цього випробування відбулася подія Аk.
Приклад. Імовірність появи події А у кожному випробуванні дорівнює Р(А) = 0,75. Необхідно змоделювати три випробування і визначити послідовність реалізації події А.
Розв’язання. Відкладемо на одиничному
відрізку числової осі точку Е = 0,75 і вважатимемо, що коли випадкове
число xі < E, то у випробуванні настала подія А. У протилежному
випадку (при 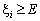 ) настала подія не А (
) настала подія не А (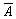 ), тобто подія А не мала місця.
), тобто подія А не мала місця.
Припустимо,
наприклад, що з відповідної таблиці обрані випадкові числа x1 = 0,925, x2 =
0,135, x3 = 0,088. Тоді за трьох випробувань отримаємо таку послідовність
реалізації подій: 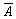 А, А.
А, А.
Моделювання сумісних (залежних і незалежних) подій можна виконати двома способами.
Перший спосіб. На першому етапі моделювання визначають усі можливі варіанти появи сумісних подій у випробуванні. Знаходять повну групу несумісних подій та обчислюють їх імовірності.
На другому етапі вчиняють так само, як і в моделюванні повної групи несумісних подій.
Приклад. Нехай при випробуванні мають місце залежні й сумісні події А та В, при цьому відомо, що Р(А) = 0,7; Р(В) = 0,5; Р(АВ) = 0,3.
Потрібно змоделювати появу подій А та В у двох випробуваннях.
Розв’язання. У кожному випробуванні можливі чотири несумісних результати, тобто настання чотирьох подій:
· С1 = АВ, Р(С1) = Р(АВ) = 0,3.
·
С2 =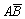 , Р(С2) = Р(
, Р(С2) = Р( ) = Р(А) – Р(ВА) = 0,7 – 0,3 =
0,4.
) = Р(А) – Р(ВА) = 0,7 – 0,3 =
0,4.
·
С3 =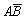 , Р(С3) = Р(
, Р(С3) = Р(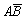 ) = Р(В) – Р(АВ) = 0,5 – 0,3 =
0,2.
) = Р(В) – Р(АВ) = 0,5 – 0,3 =
0,2.
·
С4 =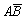 , Р(С4) = 1 – [Р(С1) + Р(С2)
+ Р(С3)] = 1 – (0,3 + 0,4 + + 0,2) = 0,1.
, Р(С4) = 1 – [Р(С1) + Р(С2)
+ Р(С3)] = 1 – (0,3 + 0,4 + + 0,2) = 0,1.
Змоделюймо повну групу подій С1, С2, С3, С4 у двох випробуваннях (прогонах). Попередньо на одиничному відрізку числової осі (рис. 5.1) послідовно відкладемо інтервали:
Dі = Р(Сі), і = 1,…, 4.

Рис. 5.1. Інтервали Dі = Р(Сі)
Нехай отримано (взято з відповідної таблиці) випадкові числа x1 = 0,68 і x2 = 0,95. Випадкове число x1 належить до інтервалу D2, тому при першому випробуванні мала місце подія А, а подія В не настала. За другого випробування випадкове число x2 належить до інтервалу D4. Обидві події А та В не мали місця.
Другий спосіб. Моделювання сумісних подій полягає у розігруванні факту появи кожної із сумісних подій окремо, при цьому, якщо події залежні, треба попередньо визначити умовні ймовірності.
Приклад. Використовуючи умови попереднього прикладу, потрібно змоделювати окрему появу подій А та В в одному випробуванні.
Розв’язання. Події А та В
є залежними, тому попередньо знаходимо умовні ймовірності Р(В/А)
та Р(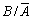 ):
):
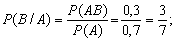
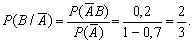
Для моделювання події А обрано випадкове число x1. Нехай x1 = 0,96. Оскільки x1>P(A), то подія А у випробуванні не настала.
Тепер розіграємо
подію В за умови, що подія А у випробуванні не мала місця. Нехай
випадкове число x2 = 0,22. Отже, 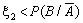 (0,22 < 2/3), тобто
маємо, що подія В за випробування настала.
(0,22 < 2/3), тобто
маємо, що подія В за випробування настала.
3. Послідовність створення математичних імітаційних моделей
У процесі створення та машинної реалізації математичних імітаційних моделей здійснюють такі (узагальнені) етапи:
· побудова концептуальної моделі;
· побудова алгоритму згідно з концептуальною моделлю системи;
· створення комп’ютерної програми;
· машинні експерименти з моделлю системи.
Побудова концептуальної моделі. Побудова концептуальної моделі складається з таких кроків:
· постановка задачі моделювання;
· визначення вимог щодо первісної інформації та способів її отримання;
· формування гіпотез і припущень;
· визначення параметрів та змінних моделі;
· обґрунтування вибору показників і критеріїв ефективності системи;
· складання змістовного опису моделі.
У здійсненні постановки задачі моделювання економічних об’єктів і процесів використовується чітке формулювання цілей і задач дослідження реальної системи, обґрунтовується необхідність імітаційного (комп’ютерного) моделювання, обирається методика розв’язування задачі з урахуванням наявних ресурсів, визначаються необхідність і можливість декомпозиції задачі на окремі взаємопов’язані підзадачі тощо.
При зборі необхідної вихідної інформації треба звертати увагу на те, що, власне, від якості вихідної інформації про об’єкт дослідження і моделювання залежить як адекватність моделі, так і достовірність результатів моделювання.
Гіпотези при побудові моделі системи слугують для заповнення «прогалин» щодо розуміння та формалізації задачі. Припущення дають можливість провести необхідні спрощення моделі на підставі раціональних гіпотез. У процесі роботи з моделлю системи, як правило, можливим є багаторазове повернення до цього етапу залежно від отриманих результатів моделювання і нової інформації (розуміння) про об’єкт.
Під час визначення параметрів і змінних складається перелік вихідних і керуючих змінних, а також зовнішніх (екзогенних) і внутрішніх (ендогенних) параметрів системи.
Обрані показники і критерії ефективності системи повинні відображати мету (цілі) функціонування системи і являти собою функції змінних і параметрів системи.
Розроблення концептуальної моделі завершується складанням змістовного опису, котрий використовується як основний документ, що характеризує результати опрацювання концептуальної постановки задачі (розуміння її всіма суб’єктами, зацікавленими у результатах дослідження).
Побудова алгоритму згідно з концептуальною моделлю системи. Побудова алгоритму містить такі складові:
· побудова логічної схеми алгоритму;
· формування математичних співвідношень (аналітичних моделей);
· перевірка достовірності алгоритму.
Спочатку, як правило, створюють узагальнену схему моделюючого алгоритму, котра задає загальний порядок (хід) дій в імітаційному моделюванні досліджуваного процесу. Після цього розробляється детальна схема, кожний елемент якої перетворюється в оператор (групу операторів) програми.
Перевірка достовірності алгоритму повинна дати відповідь на запитання, наскільки адекватно і точно він відображає сутність модельованого процесу (у конкретній ситуації) та побудованої концептуальної моделі.
Створення комп’ютерної програми. Розроблення програми для ПК включає такі кроки:
· вибір обчислювальних засобів;
· програмування (чи налаштування відповідних параметрів існуючих програмно-методичних комплексів);
· тестування програмних засобів.
На останньому кроці необхідно, зокрема, оцінити тривалість виконання програми на комп’ютері (витрати часу) для здійснення однієї реалізації (прогону) модельованого процесу, що дасть змогу системному аналітикові правильно сформулювати вимоги щодо точності й достовірності результатів моделювання.
Проведення машинних експериментів з моделлю системи. На цьому етапі провадяться серійні обчислення за допомогою програми. Етап складається з таких кроків:
· планування машинного експерименту;
· проведення робочих обчислень;
· відповідне подання результатів моделювання (у табличній та графічній формах);
· подання рекомендацій щодо оптимізації режиму функціонування реальної системи.
Перед здійсненням робочих обчислень на комп’ютері доречно скласти план проведення експерименту з переліком комбінацій змінних і параметрів, за яких повинно відбутися моделювання системи. Завдання полягає у розробці оптимального плану експерименту, реалізація якого дозволить за порівняно невеликої кількості тестувань моделі отримати достовірні дані про закономірності функціонування реальної системи.
Результати моделювання можуть бути подані у вигляді таблиць, графіків, діаграм, схем тощо. Зазвичай найпростішою формою вважаються таблиці, хоча графіки ілюструють результати моделювання економічного об’єкта (системи) у більш наочній формі. Доцільно передбачити інтерактивний режим функціонування комплексу, виведення результатів на екран дисплея та на принтер.
Інтерпретація результатів моделювання має на меті перехід від інформації, отриманої в результаті машинного експерименту з моделлю, до висновків щодо процесу функціонування об’єкта-оригіналу
4. Моделювання випадкових величин імітаційного процесу
Алгоритмічне (імітаційне) моделювання — це числовий метод дослідження систем і процесів за допомогою моделюючого алгоритму.
Кожного разу, коли на хід модельованого процесу впливає випадковий чинник, його вплив імітується за допомогою спеціально організованого розіграшу (жеребкування). Таким способом будується випадкова реалізація модельованого явища, яка є одним із результатів дослідження. За результатами окремого досліду, звичайно, не можна робити висновок щодо закономірностей досліджуваного процесу. Але за великої кількості реалізацій середні характеристики (математичне сподівання, мода, медіана), що їх виробляє (генерує) модель, набувають стійких властивостей, котрі посилюються зі зростанням кількості реалізацій (прогонів). Звісно, залишається певний ризик, який характеризується тим, що модель є гомогенною, існує неповнота даних тощо.
Кидання жеребка можна здійснити вручну (вибором із таблиці випадкових чисел), але зручніше це робити за допомогою спеціальних програм, що входять до складу програмного забезпечення комп’ютера. Такі програми називають датчиками чи генераторами випадкових чисел.
У складі трансляторів майже всіх алгоритмічних мов є стандартні процедури (чи функції), котрі генерують випадкові (точніше, псевдовипадкові) числа, що є реалізаціями послідовності випадкових чисел із рівномірним законом розподілу.
Наприклад, у складі транслятора мови Visual Basic — стандартна функція RND, що видає випадкові дійсні числа одинарної точності в інтервалі (0; 1). Звернення до цієї функції може мати вигляд x = RND, де x — можливе значення (реалізація) випадкової величини, яка рівномірно розподілена на інтервалі (0; 1).
Моделювання випадкових подій
1. Моделювання простої події. Нехай має місце подія А, імовірність настання котрої дорівнює Р(А). Потрібно обрати правило, у багаторазовому використанні якого частота появи події прямувала б до її ймовірності. Оберемо за допомогою датчика випадкових чисел, що мають рівномірний закон розподілу на інтервалі (0;1), деяке число x і визначимо ймовірність того, що x < Р(А). Для випадкового числа x, котре є реалізацією випадкової величини з рівномірним законом розподілу на інтервалі (0; 1), справедливою буде така залежність:
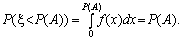
Отже, імовірність
потрапляння випадкової величини в інтервал (0; Р(А)) дорівнює
величині Р(А). Тому, якщо під час розіграшу число потрапило в цей
інтервал, то слід вважати, що відбулася подія А. Протилежна подія (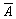 ) відбудеться з імовірністю (1 – Р(А)) у тому
разі, коли x ? Р(А).
) відбудеться з імовірністю (1 – Р(А)) у тому
разі, коли x ? Р(А).
Процедура моделювання простої події в імітаційній моделі описується алгоритмом, схема якого подана на рис. 3.2. (ДВЧ(x) — датчик випадкових чисел x, що відповідають рівномірному закону розподілу на інтервалі (0; 1).)
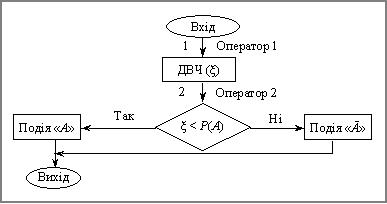
Рис. 5.2. Моделювання простої події
Оператор 1 звертається до датчика випадкових чисел, який генерує випадкове число x.
Оператор 2 здійснює перевірку умови x < Р(А). Якщо вона виконується, вважається, що відбулася подія А. У протилежному випадку вважається, що відбулася протилежна подія (А).
2. Моделювання повної групи несумісних подій. Нехай наявна повна група випадкових несумісних подій (ПГНП) А1, А2, …, Аk з імовірностями p1, p2, …, pk. При цьому виконується умова:
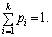
Поділимо інтервал (0; 1) на k відрізків, довжини яких відповідно дорівнюють p1, p2, …, pk.

Рис. 5.3. Моделювання повної групи несумісних подій
Якщо випадкова величина x, яка генерується датчиком випадкових чисел, що відповідають рівномірному закону розподілу на інтервалі (0; 1), припадає, наприклад, на відрізок pk–1, то це повинно означати, що відбулася подія Аk–1.
Справді, якщо
позначити  то виявиться
справедливим вираз
то виявиться
справедливим вираз 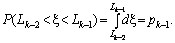
Процедура моделювання повної групи несумісних подій описується алгоритмом, схема якого наведена на рис. 5.4.
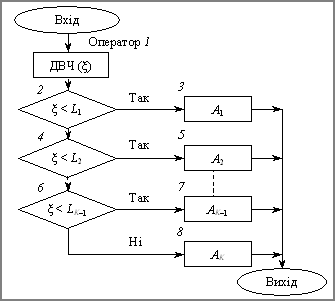
Рис. 5.4. Схема алгоритму моделювання повної групи несумісних подій
Оператор 1 звертається до генератора випадкових чисел, що відповідають рівномірному закону розподілу на інтервалі (0; 1). Оператор 2 перевіряє умову потрапляння випадкової величини x в інтервал (0; L1). Якщо ця умова виконується, то вважається, що відбулася подія А1. Якщо ця умова не виконується, то алгоритм передбачає перевірку умов потрапляння випадкової величини в інші інтервали.
3. Моделювання дискретної випадкової величини. Розподіл дискретної випадкової величини може бути поданий у вигляді таблиці
|
xi |
x1 |
x2 |
… |
xn |
|---|---|---|---|---|
|
pi |
p1 |
p2 |
… |
pn |
Тут pj — імовірність того, що випадкова величина х набуває значення хj, j = 1, …, n.
Накладається також умова:
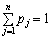 (5.8)
(5.8)
Поділимо інтервал (0; 1) на n відрізків, довжини котрих дорівнюють заданим імовірностям. Якщо випадкове число x, що формується генератором випадкових чисел, котрі відповідають рівномірному закону розподілу на інтервалі (0; 1), потрапляє до інтервалу pk, то випадкова величина х набуває значення хk. Отже, під час моделювання дискретної випадкової величини фактично використовується та сама процедура, що й за моделювання повної групи несумісних подій.
4. Моделювання випадкових величин з рівномірним розподілом. Генератор випадкових чисел генерує послідовність реалізацій випадкової величини x з рівномірною функцією розподілу на інтервалі (0; 1). Здебільшого треба моделювати випадкові величини з рівномірним розподілом, які набувають значення в інтервалі (a; b).
Припустимо, що
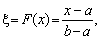
звідси
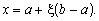
На практиці
використовується дещо модифікований спосіб. Замість меж інтервалу задаються:
середнє значення випадкової величини m(?) і величина (довжина) інтервалу
Dx, у межах якої може набувати свої значення ця випадкова величина (з
рівномірним законом розподілу). Визначення можливого значення (реалізації)
випадкової величини з рівномірним розподілом можна здійснити згідно з виразом: 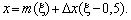
5. Моделювання випадкових величин з нормальним законом розподілу. Згідно з центральною граничною теоремою теорії ймовірностей унаслідок додавання досить великої кількості однаково розподілених незалежних випадкових величин отримуємо випадкову величину, яка має нормальний закон розподілу.
Як показали дослідження, вже внаслідок складання більш ніж десяти випадкових незалежних величин з рівномірним розподілом в інтервалі (0; 1) отримуємо випадкову величину, котру з точністю, достатньою для більшості практичних задач, можна вважати розподіленою згідно з нормальним законом.
Процедура розіграшу нормально розподіленої випадкової величини полягає у такому:
А. Складаємо, наприклад, 12
незалежних випадкових величин, які мають рівномірний закон розподілу та які
набувають значення в інтервалі (0; 1), тобто: 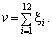
Використовуючи відомі теореми про математичне сподівання суми незалежних випадкових величин з однаковим законом розподілу та дисперсію цієї суми, легко обчислити для випадкової величини v математичне сподівання m(v) та дисперсію D(v):
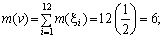
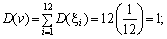

Б.Нормуємо та центруємо випадкову величину v, тобто перейдемо до випадкової величини ?, яка має нульове математичне сподівання та середньоквадратичне відхилення ?(?) = 1.

Від нормованої та центрованої випадкової величини ? можна перейти до випадкової величини у із заданими параметрами т(у) і ?(у) згідно з таким виразом:
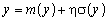
5. Приклади імітаційного моделювання
Імітаційне моделювання – один із методів дослідження складних систем, який ґрунтується на формалізації емпіричних знань про об’єкт дослідження на основі використання сучасних комп’ютерних технологій. Сутність імітаційного моделювання полягає у відтворенні за допомогою ЕОМ розгорнутого в часі процесу функціонування системи з урахуванням взаємодії із зовнішнім середовищем.
Під час імітаційного моделювання можна відтворити не лише статистичний взаємозв’язок між об’єктами системи, але й зімітувати розвиток системи в часі, що є дуже важливим для сільськогосподарських підприємств, дослідження галузевої структури яких потребує системного підходу і вимагає комплексного аналізу економічних, статистичних, картографічних та інших джерел інформації як на рівні окремого сільськогосподарського підприємства, так і на рівні адміністративних районів, областей та країни в цілому. Застосування імітаційного моделювання дасть змогу зробити об’єктивні висновки щодо тенденцій розвитку галузі, обґрунтувати доцільність виробництва того чи іншого виду продукції, стане основою для ефективного та раціонального використання існуючих ресурсів, що в кінцевому випадку призведе до гармонізації галузевої структури сільськогосподарських підприємств.
В управлінні сільськогосподарським виробництвом застосовуються системні імітаційні моделі, під час розробки яких установлюються взаємозв’язки між задачами, які описують технологічні та виробничі процеси. У даному виді моделей виділяються структурні (імітують внутрішню організацію об’єкта, процесу, явища), функціональні (описують спосіб поведінки оригіналу, його функцію) та структурно-функціональні моделі (синтез структурних та функціональних моделей).
Суть гармонізації галузевої структури сільськогосподарських підприємств полягає у приведенні сукупності одиниць, які беруть участь у виробництві продукції та послуг сільського господарства, у стан збалансованості та узгодженості, тому для побудови імітаційної моделі виробництва продукції сільського господарства доцільно застосовувати системні структурні імітаційні моделі. До визначення галузевої структури сільськогосподарських підприємств слід підходити комплексно, аналізуючи не тільки структуру товарної продукції, але й структуру витрат на виробництво продукції і послуг сільського господарства, структуру чистого доходу (виручки) від реалізації продукції, структуру посівних площ. Це дасть змогу виявити фактори, які стримують розвиток сільськогосподарського підприємства, та розробити стратегію усунення протиріч між структурними елементами. Для аналізу елементів галузевої структури доцільно використовувати ентропійний показник E(t), який визначається за формулою:
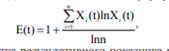
де Х – частка результативного показника у загальній структурі; n – кількість досліджуваних складових частин структури.
Значення ентропійного показника знаходиться в діапазоні від 0 до 1, для застосування ентропійного показника з метою оцінки рівня гармонізації економічних систем учені пропонують ділити його на дві частини. Перша частина інтервалом від 0 до 0,382 характеризує рівень невизначеності системи, а друга – від 0,382 до 1 – структуру системи. Поділ інтервалу у співвідношенні 0,382:0,618 називається Золотим перетином та є характеристикою гармонійного стану системи. У науці таке співвідношення відносної ентропії було названо ентропійно-гармонійною нормою організації систем (ЕГНОС).
Окрім того, використовуючи формулу ентропії (1), можна оцінити рівень спеціалізації та диверсифікації різних економічних систем, у тому числі й тих, що мають багатономенклатурну структуру (наприклад, багатогалузеві сільськогосподарські підприємства), а також визначити рівень спеціалізації чи диверсифікації районів, областей та країни в цілому. Так, якщо показник E(t) знаходиться в інтервалі від 0,25 до 1, то економічна система вважається вузькоспеціалізованою; від 0,15 до 0,25 – середньо-спеціалізованою; від 0 до 0,15 – диверсифікованою.
Для розробки імітаційної моделі гармонізації галузевої структури сільськогосподарських підприємств було обрано ПП «ХХХХ», в якому, так само як і в більшості сільськогосподарських підприємств області, існує дисбаланс галузевої структури: переважну частку чистого доходу (виручки) підприємство отримує від реалізації продукції рослинництва, при цьому галузь тваринництва залишається збитковою; більша частка у структурі витрат на виробництво припадає на прямі матеріальні витрати, а частка витрат на оплату праці, соціальні витрати та витрати на амортизацію залишається незначною (табл. 5.2).
Дослідження показали, що за традиційною методикою визначення рівня спеціалізації на основі коефіцієнта структури товарної продукції (Кс) ПП переважно має середній рівень спеціалізації (Кс знаходиться в діапазоні від 0,26 до 0,49), проте в 2008, 2010 та 2013 рр. підприємство мало високий рівень спеціалізації з переважним виробництвом зернових культур та соняшника. За ентропійним показником структури товарної продукції підприємство по всім рокам дослідження характеризується як вузькоспеціалізоване, із збалансованою та узгодженою структурою товарної продукції.
Проте дослідження інших структурних елементів сільськогосподарського підприємства вказують на недосконалість та розбалансованість його галузевої структури. Наприклад, за структурою чистого доходу (виручки) від реалізації продукції за галузями сільськогосподарського виробництва ентропійний показник знаходиться в межах від 0,77 до 1, що свідчить про високий рівень напруги всередині системи, що за умови довготермінового наближення до 1 може спричинити розпад системи, який у сільськогосподарському виробництві проявляється в падінні рівня рентабельності виробництва продукції, погіршенні стану земель, поглибленні деградаційних процесів.
Таблиця 5.2
Динаміка галузевої структури ПП «ХХХХ»
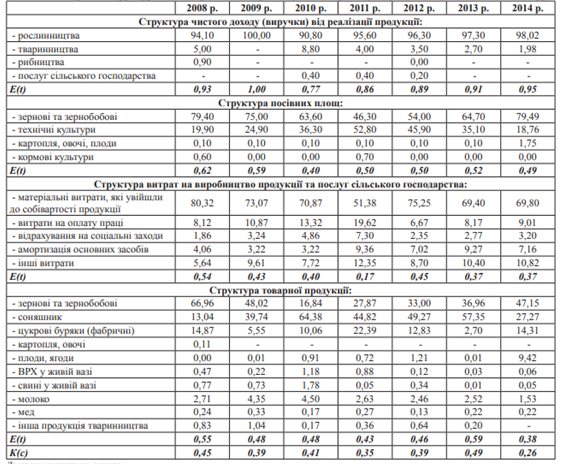
Недосконалою є й структура посівних площ: частка посівних площ під зерновими та зернобобовими культурами знаходиться в межах від 46,3% до 79,49%, частка під технічними культурами – від 18,76% до 52,8%, посівні площі під кормовими культурами відсутні або мають незначну (0,7% у 2011 р.) частку. При цьому, відповідно до нормативів, за умови спеціалізації підприємства на виробництві зерна, соняшника та продукції тваринництва частка посівних площ під зерновими культурами має знаходитись у межах від 50% до 80%, технічними – від 10% до 25%, кормовими – від 10% до 20%. Отже, враховуючи вплив багатьох факторів на галузеву структуру сільськогосподарських підприємств, застосування саме імітаційного моделювання дасть змогу здійснити експеримент з її складовими частинами.
Відомо, що сільськогосподарські показники, які застосовуються в математичному моделюванні, можна розділити на три групи. До першої групи відносяться параметри, багаторічні ряди яких підпорядковуються законам розподілу ймовірностей; до другої – параметри з невизначеністю – для них закони розподілу невідомі, а для моделювання завдаються тільки верхні та нижні значення; до третьої – параметри, між якими існують залежності.
На основі виділених груп показників можна зробити висновок, що інформація для моделювання результатів виробництва продукції сільського господарства має різний ступінь достовірності, тому для гармонізації галузевої структури необхідно застосовувати такий алгоритм імітаційного моделювання, який функціонуватиме як в умовах невизначеності, так і за наявності залежності між параметрами моделі (рис. 5.5).

Рис. 5.1. Алгоритм імітаційного моделювання виробництва продукції в сільськогосподарських підприємствах в умовах невизначеності та наявності залежності між параметрами моделі
Із метою гармонізації галузевої структури досліджуваного підприємства необхідно змоделювати ситуацію збільшення частки чистого доходу (виручки) від реалізації продукції тваринництва, а саме молока, ВРХ і свиней у живій вазі та меду, яка, своєю чергою, зумовить зміни показників інших складових частин галузевої структури підприємства. За наведеним алгоритмом доцільно формувати імітаційні моделі для кожного виду продукції. Наприклад, для формування імітаційної моделі з виробництва молока результативною ознакою обрано суму чистого доходу (виручки) від реалізації молока. Параметрами моделі є: поголів’я корів (Х1), витрати на виробництво одиниці продукції (Х2), кількість виробленої продукції в розрахунку на 1 гол. (Х3), ціна реалізації одиниці продукції (Х4). Незалежними параметрами є поголів’я корів та ціна реалізації продукції – вони визначатимуться шляхом генерації випадкових чисел за умови нормального розподілу в діапазоні від Хіmin до Хіmax, ряди для інших параметрів моделі формуватимуться на основі рівнянь, що описують залежність між змінними, наприклад Х2=f(X1).
Основою для здійснення моделювання є аналіз залежності між параметрами моделі за результатами діяльності досліджуваного сільськогосподарського підприємства з 2008 по 2014 р. (локальний рівень, варіант 1) та сільськогосподарських підприємств Харківської області в 2014 р. (регіональний рівень, варіант 2). Так, для реалізації другого варіанту алгоритму виробництва молока сільськогосподарські підприємства Харківської області були згруповані у сім груп за критерієм поголів’я корів (табл.5.3).
Таблиця 5.3
Вплив поголів’я на продуктивність корів та виробничу собівартість молока в сільськогосподарських підприємствах області за рік
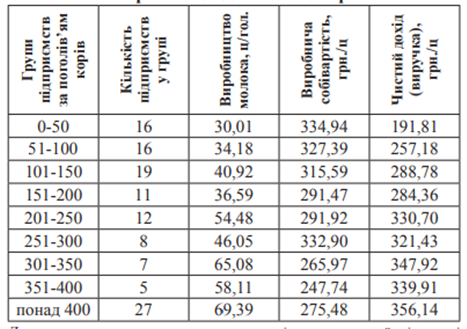
Із даних аналізу видно, що по мірі збільшення поголів’я, продуктивність корів збільшується нерівно мірно: найменший показник зафіксовано в сільськогосподарських підприємствах із чисельністю до 50 гол. – 30,01 ц/гол., найбільший – у сільськогосподарських підприємствах із чисельністю корів понад 400 гол. (69,39 ц/гол.). Зі збільшенням поголів’я зі 100 до 150 гол. відбувається зменшення виробничої собівартості, а також збільшення чистого доходу (виручки) від реалізації 1 ц молока. Аналіз показав, що між поголів’ям корів та виробництвом молока з 1 гол. існує кореляційний зв’язок (рис. 5.6).
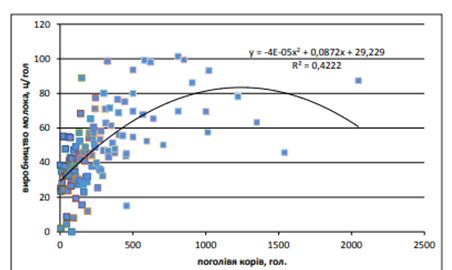
Рис.5.6. Кореляційний зв’язок між поголів’ям (х) та продуктивністю корів (у) при виробництві молока в сільськогосподарських підприємствах області за окремий рік
Варто відзначити, що продуктивність корів збільшується по мірі збільшення поголів’я до певної межі, а саме до 150 гол., потім продуктивність змінюється стрибкоподібно. Аналогічну тенденцію можна спостерігати по критерію чистого доходу (виручки) від реалізації молока, тому збільшення поголів’я корів для виробництва молока у ПП «ХХХХ» у діапазоні від 100 до 150 гол. є виправданим та може мати економічну вигоду. Поголів’я корів у ПП протягом періоду дослідження є сталим, тому при побудові імітаційної моделі в обох варіантах доцільно застосовувати рівняння залежності між поголів’ям корів та їх продуктивністю, розраховане на основі аналізу даних регіонального рівня. Дослідження зв’язку між продуктивністю корів та собівартістю 1 ц молока в ПП, показав, що між ними існує слабкий кореляційний зв’язок, який можна виразити рівнянням виду: у=0,5139х2 -32,454х+805,82.
Схожі результати показують дослідження сільськогосподарських підприємств області (рис. 5.7).
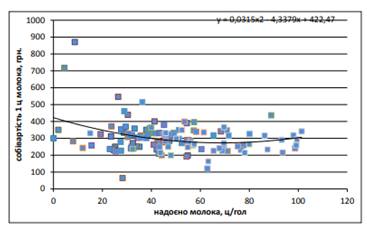
Рис. 5.7. Кореляційний зв’язок між продуктивністю корів (х) та собівартістю 1 ц молока (у) в сільськогосподарських підприємствах області за окремий рік
Ціна реалізації одиниці продукції є незалежною від інших параметрів моделі, тому її значення будуть завдані за допомогою інструменту «Генератор випадкових чисел» за умови нормального закону розподілу в діапазоні від 277,11 грн./ц до 485,25 грн. (мінімальна та максимальна ціна реалізації 1 ц молока сільськогосподарськими підприємствами).
Для проведення імітаційного моделювання науковці рекомендують проводити від 500 до 2 000 експериментів, зазначаючи, що для гарної репрезентативної вибірки достатньо провести від 200 до 500 експериментів. У даному випадку в кожній імітаційній моделі виробництва продукції тваринництва буде проведено 500 експериментів. Таким чином, можна сформулювати два варіанти вихідних даних для розробки імітаційної моделі виробництва молока у ПП (табл. 5.5). У першому варіанті використовуються рівняння залежності між поголів’ям (Х1) та продуктивністю (Х2) корів та між продуктивністю корів (Х2) та виробничою собівартістю 1ц молока (Х3) по досліджуваному підприємству (локальний рівень), у другому варіанті – залежності між тими ж параметрами на регіональному рівні (область).
Розрахунки імітаційної моделі були проведені у табличному редакторі Excel. Для виявлення некоректності у вихідних даних та помилок у постановці завдання вчені рекомендують використовувати статистичний аналіз результатів моделювання.
Таблиця 5.5
Вихідні
дані для розробки імітаційної моделі виробництва молока в
ПП «ХХХХ» з використанням залежних змінних
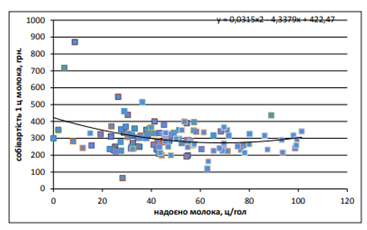
Статистичний аналіз було проведено за допомогою інструменту «Описова статистика», який дає змогу обчислити найбільш важливі для практичного аналізу характеристики розподілів. При цьому значення можуть бути визначені відразу для декількох досліджуваних змінних (табл. 5.6).
Таблиця 5.6
Статистична характеристика змінних імітаційного моделювання виробництва молока у ПП
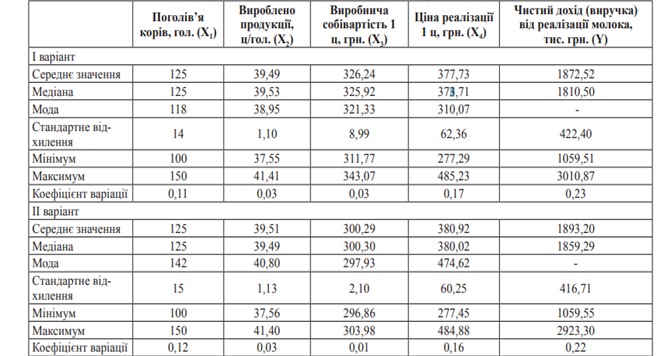
Аналіз показує, що коефіцієнт варіації параметрів моделі знаходиться в діапазоні від 0,03 (низька варіативність) до 0,23 (середня варіативність), що свідчить про те, що відхилення показників одне від одного та від середнього значення майже відсутні, а застосування рівнянь, що відображають залежності між змінним при імітаційному моделюванні, є доцільним та обґрунтованим. За наведеним алгоритмом було розроблено імітаційні моделі виробництва ВРХ та свиней у живій вазі, а також меду в ПП, що дало змогу змоделювати результати діяльності підприємства за умови збільшення поголів’я та визначити коефіцієнти галузевої структури підприємства (табл. 5.7).
Таблиця 5.7
Результати імітаційного моделювання галузевої структури ПП
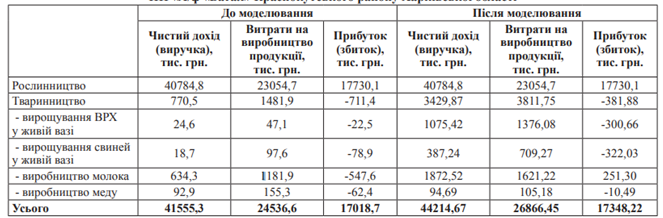
Результати імітаційного моделювання виробництва продукції сільського господарства, крім статистичного аналізу, можуть бути доповнені ймовірнісним аналізом, що забезпечить менеджера найповнішою інформацією про міру впливу ключових параметрів моделі на очікувані результати і можливі сценарії розвитку галузевої структури сільськогосподарського підприємства. У результаті проведення імітаційного моделювання підприємство за структурою товарної продукції набуло середнього рівня спеціалізації як за коефіцієнтом Кс (Кс = 0,25), так і за ентропійним показником (E(t) = 0,20). За структурою чистого доходу (виручки) підприємство також можна ідентифікувати як середньоспеціалізоване (E(t) = 0,21). У разі досягнення ентропійного показника позначки у 0,15, підприємство вважатиметься диверсифікованим.
Отже, в умовах економічного дисбалансу на локальному та регіональному рівнях, впливу багатьох факторів на результати діяльності сільськогосподарських підприємств, застосування імітаційного моделювання може стати потужним інструментом, за допомогою якого можна виявити слабкі та сильні сторони діяльності підприємства, визначити диспропорції, які гальмують його розвиток, та з високою мірою достовірності змоделювати результати виробництва продукції будь-якої галузі.
6. Концепція рейтингового управління
Природним способом зниження складності й трудомісткості управління, а отже, є зниження ступеня ризику щодо прийняття некоректних рішень, є факторизація набору показників, що дає змогу суттєво скоротити їх кількість. Така факторизація може бути здійснена в результаті заміни тієї чи іншої групи показників їх інтегрованою комплексною оцінкою. Основні критерії, що висуваються до такої оцінки:
1) загальновизнаність;
2) зрозумілість, тобто повинно бути ясно, які характерис тики та в яких саме пропорціях зосереджені в ній.
У зв’язку зі складністю одночасного контролю великої кількості різноманітних показників у фінансово-економічному аналізі значного поширення набули процедури комплексної оцінки, на підставі яких може обчислюватися рейтинг як узагальнена оцінка діяльності економічної системи (ЕС). Під рейтингом розуміють комплексну характеристику ЕС згідно з певною шкалою, де значення рейтингу — це елемент лінійно напівупорядкованої множини.
В Україні рейтингові системи лише починають використовуватися. У нас поки що немає можливості адекватно використовувати такі вельми поширені на Заході методики оцінки економічних систем, як модель Дюпона чи Z-модель Альтмана, розраховані, власне, для американських підприємств 60-х років ХХ ст. В Україні розроблена й використовується низка методик, зокрема, щодо рейтингової оцінки діяльності банків, вищих навчальних закладів тощо, зроблені перші кроки до побудови єдиної методології й методики рейтингового аналізу діяльності господарських одиниць, які були б узгоджені із західною системою стандартів і водночас ураховували б особливості вітчизняного соціально-економічного буття.
До недоліків існуючих підходів, наприклад, можна віднести:
1. Непрозорість більшості рейтингових методик оцінки економічної системи, відсутність чітких критеріїв використання їх на практиці.
2. Спотворення економічного сенсу деяких показників (що є вихідним матеріалом для обчислення рейтингів) через недосконалість існуючої системи обліку й моніторингу.
3. Орієнтація розробників методик обчислення рейтингів економічної системи на лінійні моделі взаємозв’язку показників без обґрунтування умов, у яких допускається їх застосування.
4. Обмеженість і неповнота інформаційної бази в обчисленні рейтингів через небажання керівників достатньо повною мірою та об’єктивно надавати інформацію щодо стану економічної системи.
5. У методиках, як правило, ігноруються показники, що характеризують динаміку функціонування економічної системи, а також слабоформалізовані показники (у зв’язку зі складністю їх опрацювання).
Нині відбувається процес формування методологічних засад та практики рейтингового управління.
Складність і громіздкість розв’язання перелічених вище проблем, а також зростаюча роль інформаційних технологій у прийнятті управлінських рішень визначає актуальність як проблеми розроблення теорії рейтингового управління, так і розроблення й застосування науково обґрунтованих методик.
Під рейтинговим управлінням розуміють концепцію прийняття рішень потенційними користувачами на підставі використання рейтингів у процесі реалізації функцій управління.
Із цього означення випливає, що рейтингове управління є процесом, у якому рейтинг використовується для аналізу, контролю, обліку, прогнозування та регулювання діяльності економічної системи. Суттєвою характеристикою процесу рейтингового управління є те, що рейтингова оцінка одночасно виступає як інструмент і як ціль управління.
Для конкретної економічної системи можна виокремити:
1. внутрішнє рейтингове управління;
2. зовнішнє рейтингове управління.
Об’єктом внутрішнього рейтингового управління є економічної системи та її конкуренти. Останні відіграють роль бази для порівняння. Мета внутрішнього рейтингового управління полягає у зміні іміджу економічної системи у зовнішньому середовищі.
Об’єктом зовнішнього рейтингового управління є партнери (та контрагенти) економічної системи.
7. Моделювання системи рейтингового управління та структура процесу обчислення рейтингу
Загальну структуру процесу обчислення рейтингу схематично наведено на рис.5.8. Суттєвою характеристикою методики як алгоритму є те, що характер обчислень істотно залежить від входу, тобто від вхідної інформації.
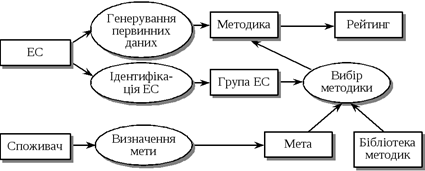
Рис. 5.8. Структура процесу обчислення рейтингу економічної системи
Можна виокремити п’ять основних етапів процесу обчислення рейтингу.
Етап 1. Підготовка первинних даних.
Деталізація цього етапу схематично показана на рис. 5.9.
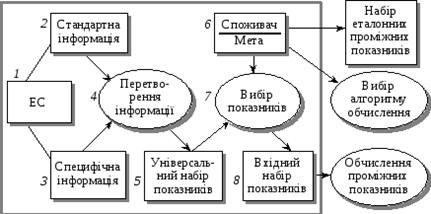
Рис. 5.9. Схема підготовки первинних даних
Етап 2. Опрацювання первинних даних.
Вихід алгоритму — набір проміжних показників, що являють собою середні значення, коефіцієнти й зведені показники. Для оцінювання набору проміжних показників здійснюють порівняльний аналіз із аналогічним, за структурою, набором проміжних показників еталонної економічної системи (чи з нормативами).
Етап 3. Статистичний аналіз.
Під час використання статистичного аналізу виникає проблема щодо порівнянності показників. Існують різні підходи залежно від змісту (семантики) інформації. Так, у фінансах використовують методологію й методи дисконтування та нарощування тощо. Цей етап припускає наявність бібліотек «стандартних» алгоритмів і програм.
Етап 4. Трендовий аналіз.
Підґрунтям трендового аналізу є моделювання прогнозного стану економічної системи. Мета трендового аналізу — оцінка можливого критичного стану економічної системи як сукупності критичних станів проміжних показників відповідно до обраного алгоритму.
Для побудови трендів зазвичай використовують методи згладжування, що ґрунтуються на обчисленні середніх (ковзних, зважених, адаптивних, експоненційних тощо).
Етап 5. Обчислення рейтингу.
Деталізація етапу зображена на рис.5.10.
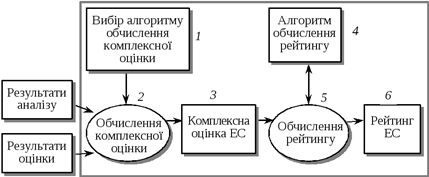
Рис. 5.10. Схема етапу визначення рейтингової оцінки
Взаємодію цих етапів схематично подано на рис. 5.9.
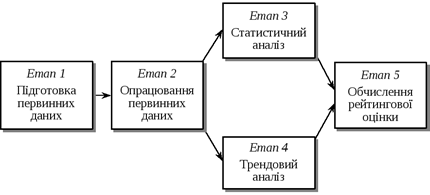
Рис. 5.9. Узагальнена схема процесу визначення рейтингу економічної системи
Підґрунтям для визначення рейтингу економічної системи є первинна інформація щодо діяльності економічної системи. Її можна поділити на стандартну й специфічну. Стандартна інформація є масивом даних, що міститься, наприклад, у трьох звітах: балансовому; щодо прибутків і збитків; руху грошових коштів. Ці звіти генеруються будь-якою економічної системи і містять основні дані стосовно до її фінансової діяльності.
Специфічна інформація є масивом даних, який міститься в решті звітів, що використовуються тією чи іншою групою ЕС. Такий набір звітів визначається специфікою діяльності, масштабом ЕС, формою власності тощо. Звіти можуть готуватись як усередині самої ЕС, так і зовні. Специфічна інформація є необхідною для визначення структури базових показників, проведення факторного аналізу їх з огляду на конкретну групу споживачів інформації щодо рейтингу ЕС. Окрім числових даних вона включає в себе результати експертного аналізу. Останні також дають можливість дослідити стан ЕС на якісному (вербальному) рівні. Хоч експертні методи відносно важко формалізувати, необхідність використання їх зумовлена тим, що вони дають можливість оцінити якість менеджменту, позиції на ринку та відповідність реального стану справ значенням показників, які декларуються, зокрема, у звітах, рекламі тощо.
Формування масиву специфічної інформації істотно залежить не лише від типу аналізованої ЕС, а й від типу споживачів рейтингу. Справді, всі основні категорії споживачів інформації стосовно стану ЕС зацікавлені в її комплексній оцінці. Однак складові цієї оцінки мають для них суттєво різну значущість.
Універсальним набором показників називають множину всіх показників, необхідних для визначення рейтингу. Універсальний набір показників формується через поєднання всіх актуальних даних, що містяться у масивах стандартної та специфічної інформації, а також зведення їх до єдиного формату.
У кожному конкретному випадку визначення рейтингу ЕС (тобто залежно від мети аналізу) з універсального набору показників формується вихідний набір показників. Він являє собою масив даних, що якнайповніше характеризують стан ЕС з погляду її наступного аналізу.
Нагадаємо, що виокремлюють два типи методик обчислення рейтингу:
1) вибір функції корисності та обчислення її значення на підставі даної комплексної оцінки;
2) обчислення рейтингу економічної системи на основі експертних процедур.
Основним недоліком методики першого типу є відносно жорстка регламентація процесу обчислення рейтингу типу функції корисності; другого типу — складність і великі витрати ресурсів у процесі обчислень. Але існують також змішані методики.
8. Моделі й методи процесу обчислення рейтингу економічної системи
Адекватною
математичною моделлю для аналізу набору показників є система S, що
визначається як n-арне відношення. Будь-яка методика обчислення рейтингу
зводиться до послідовної факторизації набору з n вихідних показників,
результатом якої є елемент лінійно впорядкованої (напівупорядкованої) множини.
Уніфікованим засобом опису процесу обчислення рейтингу на підставі аналізу
комплексних оцінок (незалежно від конкретної методики) може бути його подання у
вигляді дискретного перетворення М. Областю дії такого перетворення є п-мірний
масив А, де п — кількість використаних комплексних характеристик. Кожен індекс
масиву відповідає одній із комплексних характеристик, а значення цього індексу
— допустимі значення оцінок характеристики (обчислені за відповідною шкалою). Перетворювач М
функціонує таким чином. Якщо кількість вимірюваних характеристик дорівнює
розмірності масиву, то М просто здійснює вибір елемента масиву. Якщо ж
кількість обчислюваних характеристик менша, ніж розмірність масиву, то
перетворювач М функціонує таким чином. Нехай задано
набір значень Важливу роль у
переході від системи S до перетворювача М відіграють методи
прогнозування (як статистичні, так і експертні) та класифікація економічних
об’єктів (кластерний аналіз). Нехай U =
{u1, …, un} — універсальна множина вихідних показників. Область
значень показника ui(i = 1, …, n) позначимо через na1i
і припустимо, що Нехай Використаймо таку
форму запису: Позначимо через тоді і лише тоді,
коли для будь-яких наборів Вважатимемо, що
методики А та В 1. 2. Фактор-множина Тому доводиться
теорема 1. Якщо D —
замкнена множина і Значення теореми
1 полягає в такому. Якщо множина типових (в умовах, що розглядаються) наборів
показників належить множині У решті випадків
виникає проблема щодо обрання допустимої методики, розв’язання якої можна
отримати лише в разі використання експертних методів. Доводяться й інші важливі
теореми. Зведення проблеми
обчислення рейтингу до проблеми класифікації економічних об’єктів дає
можливість застосовувати стандартну техніку декомпозиції кваліметричних моделей
для підвищення ефективності обчислень. 
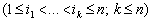 , характеристик, що
визначаються індексами
, характеристик, що
визначаються індексами 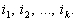 Реакцією перетворювача
М за вхідних даних
Реакцією перетворювача
М за вхідних даних 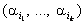 є такі три числа
є такі три числа 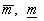 та
та 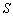 , що
, що 
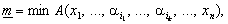 де максимум і мінімум
беруться за всіма допустимими значеннями
де максимум і мінімум
беруться за всіма допустимими значеннями 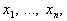 а S — середнє
значення (тобто математичне сподівання) по всіх допустимих значеннях. Числа
а S — середнє
значення (тобто математичне сподівання) по всіх допустимих значеннях. Числа  та
та 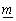 називають відповідно
оптимістичним і песимістичним рейтингами. У подальшому трійка (
називають відповідно
оптимістичним і песимістичним рейтингами. У подальшому трійка (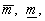 S) може бути перетворена в те чи інше число
відповідно до обраної методики.
S) може бути перетворена в те чи інше число
відповідно до обраної методики.Рейтинг як засіб класифікації економічних об’єктів. Сутність рейтингу полягає в оцінюванні позиції
аналізованого об’єкта на обраній шкалі. Ця обставина однозначно визначає
обчислення рейтингу як спеціальним чином деталізованого варіанта загальної
проблеми класифікації економічних (соціально-економічних) об’єктів. Розгляньмо
особливості цієї деталізації.
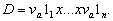
![]() — фіксована скінченна
множина методик обчислення рейтингу. Шкалу, обрану для методики
— фіксована скінченна
множина методик обчислення рейтингу. Шкалу, обрану для методики 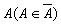 , позначимо через Шa. Таким чином, методика
, позначимо через Шa. Таким чином, методика 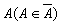 реалізує відображення
реалізує відображення 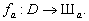
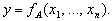
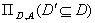 розбиття множини А,
що визначається таким чином:
розбиття множини А,
що визначається таким чином: 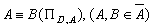
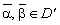 справедливим є
співвідношення
справедливим є
співвідношення 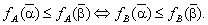
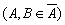 :
: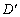 — узгоджені, якщо
— узгоджені, якщо 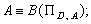
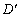 — суперечливі, якщо
— суперечливі, якщо 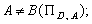
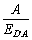 (де
(де 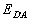 — еквівалентність, що
відповідає розбиттю
— еквівалентність, що
відповідає розбиттю 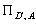 ) визначає усі типи суперечностей між методиками, які
належать до множини А та які виникають за обчислення рейтингу на множині
) визначає усі типи суперечностей між методиками, які
належать до множини А та які виникають за обчислення рейтингу на множині
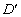 . Верхній та нижній конуси підмножини позначимо, відповідно,
через ВК(Х) та НК(Х).
. Верхній та нижній конуси підмножини позначимо, відповідно,
через ВК(Х) та НК(Х).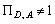 (?
(?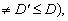 то існує такий перетин
то існує такий перетин 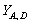 множини
множини 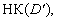 що складається з
попарно непорівнянних за включенням елементів, для котрих
що складається з
попарно непорівнянних за включенням елементів, для котрих 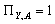 для будь-якого
для будь-якого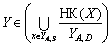 і
і 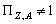 для будь-якого
для будь-якого 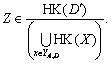
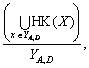 то в обчисленні
рейтингу може використовуватися будь-яка методика
то в обчисленні
рейтингу може використовуватися будь-яка методика 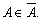
Шрифти
Розмір шрифта
Колір тексту
Колір тла
Кернінг шрифтів
Видимість картинок
Інтервал між літерами
Висота рядка
Виділити посилання
Вирівнювання тексту
Ширина абзацу