Тема 7. Наукова компонента матричного бізнес-проектування
| Сайт: | Навчально-інформаційний портал НУБіП України |
| Курс: | Економетричне моделювання наукових бізнес-проєктів☑️ |
| Книга: | Тема 7. Наукова компонента матричного бізнес-проектування |
| Надруковано: | Гість-користувач |
| Дата: | четвер, 5 лютого 2026, 03:30 |
1. Балансові моделі в проєктуванні бізнесу
Балансові моделі широко використовують в економічних дослідженнях, аналізі, проєктуванні. Ці моделі будуються на підставі балансового методу, тобто узгодженні матеріальних, трудових і фінансових ресурсів. Якщо описувати економічну систему загалом, то під балансовою моделлю мають на увазі систему рівнянь, кожне з яких виражає балансові співвідношення між виробництвом окремими економічними об’єктами обсягів продукції й сукупною потребою в цій продукції. За такого підходу розглядувана економічна система складається з об’єктів, кожен з яких випускає певний продукт, частина якого споживається ним же та іншими об’єктами системи, а решта виводиться за межі системи як її кінцева продукція. Якщо замість поняття «продукт» увести більш загальне поняття «ресурс», то під балансовою моделлю розуміють систему рівнянь, котрі задовольняють вимоги відповідності щодо наявності ресурсу та його використання. Можна також розглядати приклади балансової відповідності, як-от: відповідність наявної робочої сили й кількості робочих місць, платоспроможного попиту населення та продукції (товарів і послуг) тощо.
Розгляньмо деякі відомі види балансових моделей:
- часткові матеріальні, трудові й фінансові баланси стосовно до національної економіки чи окремих галузей (регіонів);
- міжгалузеві баланси;
- матричні бізнес-плани підприємств і фірм.
Балансові моделі на підставі звітних балансів характеризують наявні пропорції, де ресурсна частина завжди дорівнює витратній. Для виявлення диспропорцій використовують балансові моделі, в котрих фактичні ресурси узгоджувались би не тільки з їх фактичним споживанням, а й з потребою в них. Зазначимо, що балансові моделі не містять якогось механізму порівняння окремих варіантів економічних рішень (як це має місце, наприклад, у разі вибору одного з альтернативних варіантів бізнес-проекту) і не передбачують взаємозаміни різних видів ресурсів, що не дозволяє здійснити вибір оптимального варіанта розвитку економічної системи. Власне, це й визначає деяку обмеженість балансових моделей і балансового методу загалом.
Основу інформаційного забезпечення балансових моделей в економіці становить матриця коефіцієнтів витрат ресурсів за конкретними напрямами їхнього використання. Наприклад, у моделі міжгалузевого балансу таку роль відіграє так звана технологічна матриця — таблиця міжгалузевого балансу, що складається з коефіцієнтів (нормативів) прямих витрат на виробництво одиниці продукції в натуральному вираженні. З багатьох причин вихідні дані реальних господарюючих об’єктів не можуть бути використані в балансових моделях безпосередньо, тому підготовка інформації до введення в модель є досить складною проблемою. Так, для побудови моделі міжгалузевого балансу використовується специфічне поняття чистої (чи технологічної) галузі, що поєднує все виробництво певного (агрегованого) продукту незалежно від адміністративної підпорядкованості й форм власності підприємств і фірм. Перехід від господарських галузей до чистих галузей вимагає спеціального перерахунку реальних даних господарських об’єктів, наприклад, агрегування галузей, вилучення внутрішньогалузевого обігу тощо.
Балансові моделі будуються як числові матриці — прямокутні таблиці чисел. У зв’язку з цим балансові моделі належать до типу матричних економіко-математичних моделей. У матричних моделях балансовий метод дістає чітке математичне вираження. Отже, матричну структуру мають міжгалузевий і міжрегіональний баланси виробництва та розподілу продукції окремих регіонів, бізнес-планів підприємств і фірм тощо. Попри специфіку цих моделей їх об’єднує не лише спільний формальний (математичний) апарат побудови та єдиний алгоритм обчислень, а й аналогічність низки економічних характеристик. Це дає змогу розглядати структуру, зміст і основні залежності матричних моделей на прикладі міжгалузевого балансу та розподілу продукції в національній економіці. Даний баланс відображає виробництво та розподіл суспільного продукту в галузевому розрізі, міжгалузевих виробничих зв’язків, використання матеріальних і трудових ресурсів, створення й розподіл національного доходу.
Принципова схема міжгалузевого балансу (МГБ) виробництва й розподілу суспільного продукту у вартісному вираженні наведена в таблиці 7.1. У підґрунтя цієї схеми покладено поділ сукупного продукту на дві частини: проміжний і кінцевий продукт; уся національна економіка подана тут як сукупність галузей (чисті галузі). Кожна з цих галузей фігурує в балансі як виробник і як споживач. Розгляньмо схему МГБ в розрізі його блоків, що мають різний економічний зміст, — їх заведено називати квадрантами балансу (на схемі квадранти позначені римськими цифрами).
Таблиця 7.1
ПРИНЦИПОВА СХЕМА МІЖГАЛУЗЕВОГО БАЛАНСУ (МГБ)
|
Галузі-виробники |
Галузі-споживачі |
Кінцевий продукт |
Валовий продукт |
||||
|
1 |
2 |
3 |
… |
n |
|||
|
1 |
х11 |
х12 |
х13 |
… |
х1n |
Y1 |
X1 |
|
2 |
х21 |
х22 |
х23 |
… |
х2n |
Y2 |
X2 |
|
3 |
х31 |
х32 |
х33 |
… |
х3n |
Y3 |
X3 |
|
. . . |
. . . |
. . . |
. . . |
І . . |
. . . |
ІІ |
. . . |
|
n |
хn1 |
хn2 |
хn3 |
… |
хnn |
Yn |
Xn |
|
Амортизація |
C1 |
C2 |
C3 |
… |
Cn |
IV |
|
|
Оплата праці |
v1 |
v2 |
v3 |
III |
vn |
||
|
Чистий дохід |
m1 |
m2 |
m3 |
… |
mn |
||
|
Валовий продукт |
X1 |
X2 |
X3 |
… |
Xn |
|
|
Коефіцієнти прямих і повних матеріальних витрат. Здійснюючи аналіз моделі міжгалузевого балансу, потрібно розглянути основні властивості матриці коефіцієнтів прямих матеріальних витрат А. Ці коефіцієнти за визначенням є невід’ємними, отже, матриця А в цілому є невід’ємною: А ? 0. Процес відтворення не можна було б здійснити, якщо б для власного відтворення в галузі витрачався більший обсяг продукту, ніж створювався. Звідси очевидно, що діагональні елементи матриці А менші ніж одиниця: aii <1, i = 1, ..., n.
Обчислювальні аспекти розв’язування задач на підставі моделі МГБ.
|
Галузі-виробники |
Галузі-споживачі |
Кінцева продукція |
Валова продукція |
||
|
1 |
2 |
3 |
|||
|
1 |
232,6 |
51,6 |
291,8 |
200,0 |
775,3 |
|
2 |
155,1 |
255,0 |
0,0 |
100,0 |
510,1 |
|
3 |
232,6 |
51,0 |
145,9 |
300,0 |
729,6 |
|
Умовно чиста продукція |
155,0 |
153,1 |
291,9 |
600,0 |
|
|
Валова продукція |
775,3 |
510,1 |
729,6 |
|
2015,0 |
Перший квадрант МГБ — це таблиця міжгалузевих потоків. Показники, що містяться на перетині рядків і стовпців, є обсягами міжгалузевих потоків продукції xij, i та j — відповідно номери галузей виробників і споживачів. Перший квадрант за формою є квадратною матрицею n-го порядку, сума всіх елементів якої дорівнює річному засобу відтворення амортизації засобів виробництва у матеріальній сфері.
У другому квадранті подана кінцева продукція всіх галузей матеріального виробництва, де під кінцевою продукцією мається на увазі продукція, що виходить зі сфери виробництва в кінцеве використання (на споживання та накопичення). У табл. 8.1 цей розділ подано в узагальненому вигляді як один стовпчик величин Yі,; у розгорнутій схемі балансу кінцевий продукт кожної галузі можна подати диференційовано за напрямами використання: на особисте споживання населення, суспільне споживання, на накопичення, покриття збитків, експорт тощо.
Третій квадрант МГБ також характеризує національний дохід, але з боку його вартісного складу — як суму чистої продукції й амортизації; чисту продукцію тлумачать як суму оплати праці та чистого доходу галузей. Обсяг амортизації (Cj) та чистої продукції (vj + mj) деякої галузі називають умовно чистою продукцією цієї галузі й позначають у подальшому через Zj.
Четвертий квадрант відбиває розподіл і використання національного доходу. В результаті перерозподілу створеного національного доходу утворюються скінченні доходи населення, підприємств, держави.
Дані четвертого квадранта важливі для відображення в міжгалузевій моделі балансу доходів і витрат населення, джерел фінансування капіталовкладень, поточних витрат невиробничої сфери, для аналізу загальної структури доходів за групами споживачів. Загалом МГБ у межах єдиної моделі об’єднує баланси галузей матеріального виробництва, баланс сукупного суспільного продукту, баланс національного доходу, баланс доходів і витрат населення.
Якщо, як показано в табл. 7.1, позначити валовий продукт j-ї галузі літерою Xj, то можна записати два співвідношення, що відбивають сутність МГБ та є підґрунтям його економіко-математичної моделі.
По-перше, розглядаючи схему балансу по стовпчиках, можна зробити висновок, що сума матеріальних витрат будь-якої галузі-споживача та її умовно чистий продукт дорівнює валовій продукції цієї галузі:
Xj
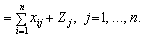 (7.1)
(7.1)
По-друге, розглядаючи МГБ по рядках для кожної галузі-виробника, бачимо, що валова продукція будь-якої галузі дорівнює сумі матеріальних витрат галузей, які споживають її продукцію, і кінцевої продукції даної галузі:
Xi  (7.2)
(7.2)
Підсумовуючи за j систему рівнянь (7.1),
дістаємо 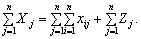
Аналогічно, підсумовуючи за i систему
рівнянь (7.2), дістаємо 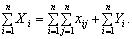
Звідси легко помітити, що 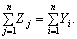 (7.3)
(7.3)
Це рівняння показує, що в міжгалузевому балансі виконується принцип еквівалентності матеріального та вартісного складу національного доходу.
Припускається гіпотеза, згідно з якою для виробництва одиниці продукції в j-й галузі необхідна певна кількість витрат проміжної продукції і-ї галузі, що становить aij, і ця величина не залежить від обсягів виробництва в j-й галузі та є досить стабільною величиною в часі. Величини aij називають коефіцієнтами прямих матеріальних витрат та обчислюють таким чином:
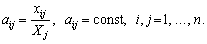 (7.4)
(7.4)
Коефіцієнти прямих матеріальних витрат показують, яку кількість продукції і-ї галузі необхідно витратити, якщо враховувати лише прямі витрати, для виробництва одиниці продукції j-ї галузі. З урахуванням формули (7.4) систему рівнянь балансу (8.2) можна записати у вигляді
Хі
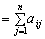 Хі
Хі
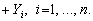 (7.5)
(7.5)
Якщо ввести до розгляду матрицю коефіцієнтів прямих матеріальних витрат А = (аij), вектор-стовпчик валової продукції X та вектор-стовпчик кінцевої продукції Y:
 то система рівнянь (8.5) у матричній формі матиме вигляд
то система рівнянь (8.5) у матричній формі матиме вигляд
X = AX + Y . (7.6)
Систему рівнянь (7.5), чи у матричній формі (7.6), називають економіко-математичною моделлю міжгалузевого балансу (моделлю Леонтьєва, моделлю «витрати — випуск»). За допомогою цієї моделі можна виконати три варіанти обчислень:
- задаючи в моделі обсяги валової продукції кожної галузі (Хi), можна визначити обсяги кінцевої продукції кожної галузі(Yi):
Y = (E – A)X, (7.7)
де Е — одинична матриця n-го порядку;
- задаючи обсяги кінцевої продукції всіх галузей (Yi), можна визначити обсяги валової продукції кожної галузі (Хi):
X = (E – A)–1Y; (7.8)
- для низки галузей задаючи обсяги валової продукції, а для решти — обсяги кінцевої продукції, можна відшукати величини кінцевої та валової продукції всіх галузей.
У формулах (7.7) та (7.8) Е позначає одиничну матрицю n-го порядку, а (Е – А)–1 — матрицю, обернену до матриці (Е – А).
Якщо визначник матриці (Е – А) не дорівнює нулеві, тобто ця матриця не вироджена, тоді існує матриця, обернена до неї. Позначимо цю матрицю через В:
B = (Е – А)–1. (7.9)
Систему рівнянь у матричній формі (8.8) можна записати:
X = BY . (7.10)
Елементи матриці В позначатимемо через bij , тоді з матричного рівняння (8.10) для будь-якої і-ї галузі можна отримати співвідношення:
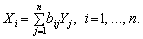 (7.11)
(7.11)
Із співвідношення (7.11) випливає, що валова продукція постає як зважена сума обсягів кінцевої продукції, ваговими коефіцієнтами тут є bіj, котрі показують, скільки всього необхідно виробити валової продукції і-ї галузі для випуску у сферу кінцевого використання одиниці продукції j-ї галузі. На відміну від коефіцієнтів прямих витрат aij , коефіцієнти bіj називають коефіцієнтами повних матеріальних витрат, і вони включають у себе як прямі, так і опосередковані витрати всіх порядків. Якщо прямі витрати відбивають кількість засобів виробництва, використаних безпосередньо на виготовлення певних обсягів даного продукту, то опосередковані стосуються попередніх стадій виробництва і входять у виробництво продукції не прямо, а через інші (проміжні) засоби виробництва.
Коефіцієнти повних матеріальних витрат bij показують, який обсяг продукції j-ї галузі необхідно виробити, щоб з урахуванням прямих і опосередкованих витрат цієї продукції отримати одиницю кінцевої продукції j-ї галузі.
Коефіцієнти повних матеріальних витрат можна застосовувати, коли необхідно визначити, як вплинуть на валовий випуск певної галузі деякі зміни щодо обсягів випуску кінцевої продукції всіх галузей:
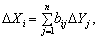 (7.12)
(7.12)
де DXi та DYj — зміни (прирости) обсягів валової й кінцевої продукції відповідно.
Система рівнянь міжгалузевого балансу відображає реальні економічні процеси, в котрих сенс можуть мати лише невід’ємні значення валових випусків; таким чином, вектор валової продукції складається з невід’ємних компонентів вектора Х, який є невід’ємним вектором: X > 0. Постає питання, за яких умов економічна система здатна забезпечити невід’ємний кінцевий випуск у всіх галузях? Відповідь на це питання пов’язана з поняттям продуктивності матриці коефіцієнтів прямих матеріальних витрат.
Означення. Називатимемо невід’ємну матрицю А продуктивною, якщо існує такий невід’ємний вектор Х, що
X > AX. (7.13)
Очевидно, що умова (7.13) означає існування невід’ємного вектора кінцевої продукції Y > 0 для моделі міжгалузевого балансу (7.6).
Щоб матриця коефіцієнтів прямих матеріальних витрат А була продуктивною, необхідно і достатньо, аби виконувалася одна з перелічених нижче умов:
- матриця (Е – А ) має бути невід’ємно оберненою, тобто повинна існувати обернена матриця (Е – А) –1 ? 0;
-
матричний ряд 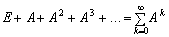 має збігатися, Ak ® 0, k ® ?,
а його сума дорівнює оберненій матриці (Е – А)–1;
має збігатися, Ak ® 0, k ® ?,
а його сума дорівнює оберненій матриці (Е – А)–1;
-
найбільший за модулем l розв’язок (власне значення)
характеристичного рівняння 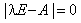 має бути строго меншим від одиниці;
має бути строго меншим від одиниці;
- усі головні мінори матриці (Е – А), тобто визначники матриць, що утворені елементами перших рядків і перших стовпчиків цієї матриці порядку від 1 до n, мають бути додатними.
Більш простою, але лише достатньою ознакою продуктивності матриці А є обмеження на величину її норми, тобто на величину найбільшої із суми елементів матриці А в кожному стовпчику. Якщо норма матриці А строго менша від одиниці, то ця матриця є продуктивною. Наголосимо, що дана умова є лише достатньою, і матриця А може виявитися продуктивною й у разі, якщо її норма буде більшою за одиницю.
Найбільший за модулем корінь характеристичного рівняння, наведеного в третій умові продуктивності матриці А (позначимо його через l*), може слугувати за оцінку загального рівня коефіцієнтів прямих матеріальних витрат, а отже, величина (1 – l*) характеризує залишок після витрат, тобто продуктивність. Чим більшим є (1 – l*), тим більшими є можливості досягнення інших цілей, окрім поточного виробничого процесу. Іншими словами, чим вищим є загальний рівень коефіцієнтів матриці А, тим більшим — максимальне за модулем власне значення (l* ) і нижчим — рівень продуктивності, і навпаки, чим нижчий загальний рівень коефіцієнтів матриці А, тим меншим є максимальне по модулю власне значення (l* ) і вищою продуктивність.
Проаналізуймо матрицю коефіцієнтів повних матеріальних витрат, тобто матрицю В = (Е – А)–1. Елемент цієї матриці bijпоказує, скільки всього необхідно виробити продукції і-ї галузі, щоб одержати одиницю кінцевої продукції j-ї галузі.
Дамо інше означення коефіцієнта повних матеріальних витрат з огляду на те, що окрім прямих витрат існують опосередковані витрати тієї чи іншої продукції для виробництва продукції даної галузі. Розгляньмо для прикладу формування витрат електроенергії на випуск стального прокату, обмежуючись технологічним ланцюжком «руда—чавун—сталь—прокат». Витрати електроенергії для отримання прокату зі сталі називатимемо прямими витратами, ті самі витрати для отримання сталі з чавуну — опосередненими витратами 1-го порядку, а витрати електроенергії для отримання чавуну з руди — опосередкованими витратами електроенергії на випуск сталевого прокату 2-го порядку тощо. Отже, можна дати таке означення:
Коефіцієнтом квазіповних матеріальних витрат cij називають
суму прямих і опосередкованих витрат продукції і-ї галузі для
виробництва одиниці продукції j-ї галузі через проміжні продукти на
всіх попередніх стадіях виробництва. Якщо коефіцієнти опосередкованих
матеріальних витрат k-го порядку позначати через
, 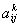 то
має місце формула
то
має місце формула
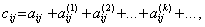 (7.14)
(7.14)
a якщо ввести до розгляду матрицю коефіцієнтів квазіповних
матеріальних витрат C = (cij) та матриці
коефіцієнтів опосередкованих матеріальних витрат різних порядків 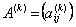 , то
поелементну формулу (7.14) можна подати в матричній формі:
, то
поелементну формулу (7.14) можна подати в матричній формі:
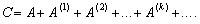 (7.15)
(7.15)
З огляду на змістовну суть коефіцієнтів опосередкованих матеріальних витрат можна записати такі математичні співвідношення:
за використання котрих матрична формула (7.15) набирає вигляду
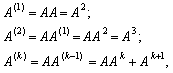 (7.16)
(7.16)
Якщо матриця коефіцієнтів прямих матеріальних витрат А є продуктивною, то з другої умови продуктивності існує матриця В = (Е – А)–1, яка є сумою збіжного матричного ряду:
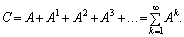 (7.17)
(7.17)
Порівнюючи вирази (7.16) та (7.17), дістанемо:
В = Е + С,
або в поелементному записі: 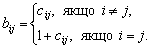
Це визначає економічний сенс, що пояснює відмінність між коефіцієнтами (елементами) матриць В та С: на відміну від коефіцієнтів матриці С, що враховують лише витрати на виробництво продукції, коефіцієнти матриці В включають у себе, окрім витрат, також одиницю кінцевої продукції, котра виходить за сферу виробництва.
Основний обсяг обчислень за моделлю МГБ пов’язаний з обчисленнями матриці коефіцієнтів повних матеріальних витрат В. Якщо матриця коефіцієнтів прямих матеріальних витрат А задана та є продуктивною, то матрицю В можна обчислювати за допомогою формул обернення матриць, що розглядаються в курсі матричної алгебри, або наближеним способом, використовуючи розклад у матричний ряд (7.17).
Розглянемо перший спосіб знаходження матриці В. Знаходимо матрицю (Е – А), а потім, застосовуючи один із прямих методів пошуку обернених невироджених матриць, обчислюємо матрицю (Е – А)–1. Одним із широковживаних методів обернення матриць є метод Жордана. Використовують також метод, що ґрунтується на застосуванні формули
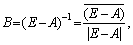 (7.18)
(7.18)
де в чисельнику — матриця, приєднана до матриці (Е – А),
елементи котрої є алгебраїчними доповненнями для елементів транспонованої
матриці (Е – А)?, а в знаменнику — визначник матриці (Е – А).
Алгебраїчні доповнення, у свою чергу, для елементів з індексами і та j дістають
множенням співмножника 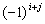 на
мінор, що отримується після викреслювання з матриці А і-го
рядка й j-го стовпчика.
на
мінор, що отримується після викреслювання з матриці А і-го
рядка й j-го стовпчика.
Згідно з другим способом обчислення матриці коефіцієнтів повних матеріальних витрат використовують формулу (7.17). Обов’язковою умовою коректності цих обчислень є умова щодо продуктивності матриці А, а, здійснюючи обчислення, обмежуються врахуванням опосередкованих матеріальних витрат до певного порядку (наприклад 3-го порядку). Тут використовується процедура множення квадратних матриць з їхнім наступним додаванням, а коефіцієнти повних матеріальних витрат отримуються з деяким наближенням (із заниженням).
Приклад Для тригалузевої економічної системи задані матриця коефіцієнтів прямих матеріальних витрат і вектор кінцевої продукції:
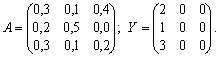
Необхідно обчислити коефіцієнти повних матеріальних витрат і вектор валової продукції, а також заповнити схему міжгалузевого матеріального балансу.
Розв’язання.
1. Визначимо матрицю коефіцієнтів повних матеріальних
витрат згідно з другим (наближеним) способом, ураховуючи опосереднені
матеріальні витрати до 2-го порядку включно. Запишемо матрицю коефіцієнтів опосередкованих
витрат 1-го порядку: 
матрицю коефіцієнтів опосередкованих витрат 2-го порядку:
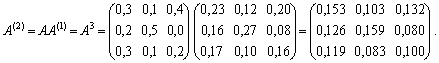
Отже, матриця коефіцієнтів повних матеріальних витрат
наближено дорівнюватиме: 
2. Обчислимо матрицю коефіцієнтів повних матеріальних витрат за допомогою формул обернення невироджених матриць (перший спосіб):
а) знаходимо матрицю (Е – А): 
б) обчислимо визначник цієї матриці: 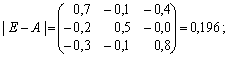
в) транспонуємо матрицю (Е – А): 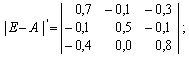
г) знайдемо алгебраїчні доповнення для елементів матриці
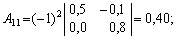
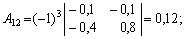
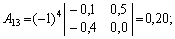
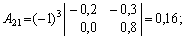
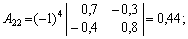
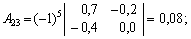
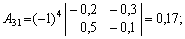

Отже, приєднана до матриці (Е – А)
матриця має вигляд: 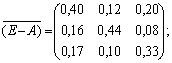
д) використовуючи формулу (7.18), знаходимо матрицю
коефіцієнтів повних матеріальних витрат: 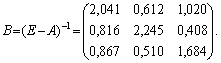
Як зазначалося, елементи матриці В, що обчислені згідно з першим способом, є дещо більшими, ніж відповідні елементи матриці, обчисленої згідно з другим (наближеним) способом.
3. Знаходимо обсяги валової продукції трьох галузей
(вектор Х), використовуючи формулу (7.10): 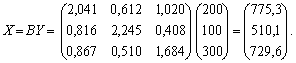
4. Для обчислення елементів першого квадранта матеріального міжгалузевого балансу скористаємося формулою, що випливає з (7.4), тобто xij = aijXj, i, j = 1, …, n.
Для отримання елементів першого квадранта необхідно елементи першого стовпчика матриці А перемножити на величину X1 = 775,3, елементи другого стовпчика матриці А — на X2 = 510,1; елементи третього стовпчика матриці А — на X3 = 729,6.
Складові третього квадранта (умовно чиста продукція) знаходять з урахуванням формули (7.1) як різницю між обсягами валової продукції та сумами елементів відповідних стовпчиків відшуканого першого квадранта.
Четвертий квадрант у наведеному прикладі складається лише з одного показника й слугує, зокрема, для контролю правильності обчислень: сума елементів другого квадранта повинна (у вартісному матеріальному балансі) збігатися із сумою елементів третього квадранта.
2. Балансові моделі в аналізі і прогнозуванні економічних показників
Різноманітні модифікації моделі міжгалузевого балансу виробництва й розподілу продукції в національній економіці дозволяють розширити коло показників, що їх охоплює модель. Розгляньмо застосування міжгалузевого балансового методу для аналізу таких важливих економічних показників, як праця, засоби, ціни.
Важливими аналітичними можливостями даного методу є, зокрема, визначення прямих і повних витрат праці на одиницю продукції та розроблення на підставі цього балансових продуктово-трудових моделей; вихідною моделлю тут слугує звітний міжпродуктовий баланс у натуральному вираженні.
Позначимо витрати живої праці для виробництва j-го продукту через Lj, а обсяг виробництва цього продукту (валовий випуск), як і раніше, через Xj, тоді прямі витрати праці на одиницю j-го виду продукції (коефіцієнта прямої трудомісткості) можна подати формулою:
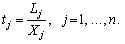 (7.19)
(7.19)
Уведемо таке поняття, як повні витрати праці — сума прямих витрат живої праці та витрат уречевленої праці, які переносяться на продукт через використані засоби виробництва. Якщо позначити величину повних витрат праці на одиницю продукції j-го виду через Tj, то добутки aij Tj відбивають затрати уречевленої праці, перенесеної на одиницю j-го продукту через і-й засіб виробництва. Припускається, що коефіцієнти прямих матеріальних витрат aij виражені в натуральних одиницях. Тоді повні трудові витрати на одиницю j-го виду продукції (коефіцієнти повної трудомісткості) дорівнюватимуть:
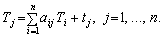 (7.20)
(7.20)
Уведемо до розгляду вектор-рядок коефіцієнтів прямої
трудомісткості 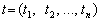
i вектор-рядок коефіцієнтів повної трудомісткості 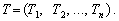
Тепер, із використанням розглядуваної вище матриці
коефіцієнтів прямих матеріальних витрат А (у натуральному
вираженні), систему рівнянь (8.20) можна подати в матричному вигляді: 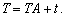 (7.21)
(7.21)
Виконавши відповідні математичні перетворення з використанням
одиничної матриці Е, а власне: 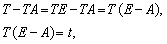
дістанемо таке співвідношення: 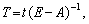 (7.22)
(7.22)
де 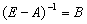 є матрицею коефіцієнтів повних матеріальних витрат, отже,
є матрицею коефіцієнтів повних матеріальних витрат, отже,
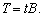 (7.23)
(7.23)
Позначимо через L величину сукупних витрат живої праці за всіма видами продукції, котрі з урахуванням (8.19) дорівнюватимуть
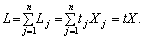 (7.24)
(7.24)
Використовуючи співвідношення (7.24), (7.23) та (7.10), дістанемо:
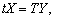 (7.25)
(7.25)
де t і Т — вектор-рядки коефіцієнтів прямої та повної трудомісткості, а Х та Y — вектор-стовпці валової та кінцевої продукції відповідно.
Рівняння (7.25) є основним балансовим рівнянням у теорії міжгалузевого балансу праці. Його конкретний економічний сенс полягає в тому, що вартість кінцевої продукції, яка оцінена за повними витратами праці, дорівнює сукупним затратам живої праці. Порівнюючи споживчий ефект різних взаємозамінюваних продуктів з повними трудовими витратами на їх випуск, можна аналізувати порівняльну ефективність їх виробництва.
За допомогою показників повної трудомісткості більш повно й точно, ніж за використання існуючих вартісних показників, виявляється структура витрат на випуск різних видів продукції, а також співвідношення між витратами живої й матеріалізованої праці.
На підставі використання коефіцієнтів прямої та повної трудомісткості можуть розроблятися міжгалузеві й міжпродуктові баланси витрат праці та використання трудових ресурсів. Схематично ці баланси будуються за спільним типом матричних моделей, а всі показники в них (міжгалузеві зв’язки, кінцевий продукт, умовно чиста продукція тощо) виражаються в трудових вимірювачах.
Приклад
Нехай у доповнення до вихідних даних попереднього прикладу, задані також витрати живої праці (трудові ресурси) в розрізі трьох галузей: L1 = 1160; L2 = 460; L3 = 875 — в однакових одиницях вимірювання. Треба визначити коефіцієнти прямої та повної трудомісткості й скласти міжгалузевий баланс витрат праці.
Розв’язання.
1. Скориставшись формулою (7.19) та розв’язком
попереднього прикладу, знайдемо коефіцієнти прямої трудомісткості: 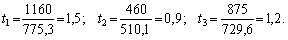
2. За формулою (7.23) знайдемо коефіцієнти повної трудомісткості: 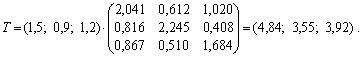
3. Перемножуючи відповідно перший, другий і третій рядки першого та другого квадрантів міжгалузевого матеріального балансу, побудованого в попередньому прикладі, на відповідні коефіцієнти прямої трудомісткості, отримаємо схему міжгалузевого балансу праці (в трудових вимірниках) (табл. 7.3).
Таблиця 7.3
МІЖГАЛУЗЕВИЙ БАЛАНС ВИТРАТ ПРАЦІ
|
Галузі-виробники |
Галузі-споживачі |
Витрати праці на кінцеву продукцію |
Витрати праці в галузях (трудові ресурси) |
||
|
1 |
2 |
3 |
|||
|
1 |
348,9 |
76,5 |
437,7 |
300,0 |
1163,0 |
|
2 |
139,6 |
229,5 |
0,0 |
90,0 |
459,1 |
|
3 |
279,1 |
61,2 |
175,1 |
360,0 |
875,5 |
Незначні розходження між даними таблиці та вихідними даними зумовлені похибками заокруглення в обчисленнях.
Розвиток основної (базової) моделі міжгалузевого балансу
знайшов своє втілення також завдяки включенню в неї показників капіталомісткості продукції. В
найпростішому випадку модель доповнюється окремим рядком, в якому подані у
вартісному вираженні обсяги виробничих засобів Фj, задіяних у
кожній j-й галузі (j = 1, …, n). На
підставі цих даних та обсягів валової продукції всіх галузей визначаються
коефіцієнти прямої капіталомісткості продукції j-ї
галузі: 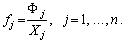 (7.26)
(7.26)
Коефіцієнт прямої капіталомісткості показує обсяг виробничих
засобів, безпосередньо задіяних у виробництві в даній галузі, в розрахунках на
одиницю її валової продукції. На відміну від цього показника коефіцієнт повної
капіталомісткості Fj відображає обсяг засобів, необхідних у
всіх галузях для випуску одиниці кінцевої продукції j-ї галузі (j =
1, …, n). Якщо aij — коефіцієнти прямих
матеріальних витрат, то для коефіцієнтів повної капіталомісткості справедливою
буде рівність, аналогічна рівності (7.20) для коефіцієнтів повної
трудомісткості: 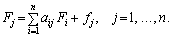 (7.27)
(7.27)
Якщо ввести до розгляду вектор-рядок коефіцієнтів прямої
капіталомісткості
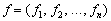 і
вектор-рядок коефіцієнтів повної капіталомісткості
і
вектор-рядок коефіцієнтів повної капіталомісткості 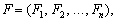 то
систему рівнянь (7.27) можна переписати в матричній формі:
то
систему рівнянь (7.27) можна переписати в матричній формі:
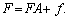 (7.28)
(7.28)
Звідси за допомогою перетворень, аналогічних використовуваним вище щодо коефіцієнтів трудомісткості, можна отримати матричне співвідношення
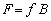 , (7.29)
, (7.29)
де B = (E – A) –1 — матриця коефіцієнтів повних матеріальних витрат.
Для глибшого аналізу потрібно деталізувати засоби на основні та обігові, а в межах основних — на будівлі, споруди, виробниче устаткування, транспортні засоби тощо.
Нехай у цілому всі виробничі засоби деталізовано на m груп. Тоді характеристика задіяних у народному господарстві засобів задається матрицею показників Фkj , що відображають обсяг засобів k-ї групи, задіяних у j-й галузі:
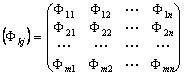 .
.
Коефіцієнти прямої капіталомісткості також утворюють матрицю
розмірності m ? n, елементи котрої визначають
обсяги виробничих засобів k-ї групи, безпосередньо використовуваних
у виробництві одиниці продукції j-ї галузі: 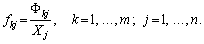
Для кожної j-ї галузі можна обчислити коефіцієнти повної капіталомісткості Fkj, що відображають повну потребу в засобах k-ї групи для випуску одиниці кінцевої продукції цієї галузі:
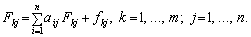 (7.30)
(7.30)
Розв’язок системи рівнянь (8.30) дозволяє подати коефіцієнти повної капіталомісткості за кожною з груп засобів як функцію коефіцієнтів прямої капіталомісткості:
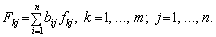 (7.31)
(7.31)
У формулах (7.30) та (7.31) величини aij та bij — це вже відомі коефіцієнти прямих і повних матеріальних витрат.
Коефіцієнти капіталомісткості в міжгалузевому балансі дозволяють узгодити планований випуск продукції з наявними виробничими потужностями. Зокрема, потреба у функціонуючих засобах k-ї групи для отримання запланованого обсягу матеріального виробництва Xj, j = 1, …, n по всіх галузях задається формулою:
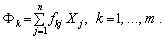 (7.32)
(7.32)
3. Застосування балансових моделей у задачах маркетингу
Розгляньмо розв’язування однієї із задач маркетингу на підставі моделі міжгалузевого балансу.
У моделях міжпродуктових балансів до обсягів кінцевої продукції Yi, як правило, входить обсяг продукції, що спрямовується на приріст запасів і резервів. Обсяги цього приросту за кожним видом продукції часто задаються поза моделлю (екзогенно), що визначає загальний обсяг продукції кожного найменування, котрий іде на приріст запасів, але не дає можливості дізнатися, в якому саме обсязі необхідні ці запаси для забезпечення неперервності виробництва, якими повинні бути оптимальні обсяги сукупних запасів. Аби відповісти на ці запитання, треба разом з прямими витратами відображати обсяги запасів і резервів у тому розділі балансу, де у рядках розміщені виробничі зв’язки та витрати, а у стовпчиках — витрати різних продуктів на виробництво продукту даного виду.
Ці проблеми можна вирішити введенням так званих коефіцієнтів капіталомісткості.
Означення. Коефіцієнт капіталомісткості Sij показує, який обсяг запасу продукції і-го виду потрібно мати у виробництві одиниці продукції j-го виду. Якщо Sij — це величина запасу продукції i-го виду, що використовується для виробництва j-ї продукції, а Xj — загальний обсяг виробництва j-ї продукції, то величину коефіцієнта капіталомісткості можна визначити таким чином:
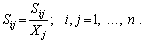 (7.33)
(7.33)
На практиці коефіцієнти капіталомісткості можна обчислити на підставі статистичних даних за попередні роки.
Якщо до схеми міжпродуктового балансу ввести показник капіталомісткості, то рівняння (8.5) (підрозд. 8.2) матиме вигляд
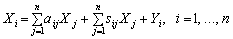 (7.34)
(7.34)
або у матричному вигляді:
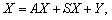 (7.35)
(7.35)
де S = (sij) — матриця коефіцієнтів капіталомісткості. Звідси маємо:
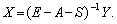 (7.36)
(7.36)
Матриця BS = (E – A – S)–1 аналогічна матрицi (В) коефіцієнтів нових матеріальних витрат. Поряд з прямими та опосередкованими витратами вона містить також обсяги запасів на одиницю кінцевої продукції.
Балансові моделі можуть бути корисними й у реалізації збутової функції маркетингу, зокрема в питаннях ціноутворення. В умовах формування ринкових цін ці моделі допомагають, наприклад, виявити дисбаланс міжгалузевих і внутрішньогалузевих цін в умовах вільного ринкового ціноутворення.
4. Бізнес план як матриця бізнес-проєкту
Бізнес-план є головним документом, який у стислій форми презентує проект та містить його обґрунтування, що дозволяє інвесторам оцінити ефективність інвестицій. Загалом, недооцінка важливості бізнес-планування або поверхове ставлення до нього є достатньо розповсюдженою помилкою не тільки в бізнесовому підприємництві. Наслідком такого хибного ставлення є породження ілюзій щодо можливостей та перспектив проекту, відсутність чіткого уявлення щодо етапів його реалізації, недооцінка ризиків, неготовність менеджерів, що займаються реалізацією проекту до непередбаченого розвитку подій та в кінцевому підсумку крах надій та вкладених ресурсів. Отже, головним завданням бізнес-плану є надати цілісну, системну, науково обґрунтовану оцінку проекту. При цьому для різних суб’єктів він виконує різні функції: для інвестора – це інструмент оцінки ефективності вкладення капіталу; для підприємця – програма дій щодо реалізації проекту; для державних органів – засіб регулювання та контролю відносин у відповідній сфері. Розробка бізнес-плану дозволяє спрогнозувати та заздалегідь спланувати різні варіанти конкурентної стратегії підприємства тобто здійснювати сценарне планування. Також, важливою рисою планування є можливість порівнювати заплановані або прогнозні показники діяльності з реальними.
Зауважимо, що не існує єдиної методики складання бізнес-плану, проте у світовій практиці найбільш розповсюдженими є методики UNIDO (The United Nations Industrial Development Organization – Організація ООН щодо промислового розвитку), методики запропоновані ЄБРР та TACIS (Technical Assistance to the Commonwealth of Independent States – Технічна допомога для країн СНД). Слід пам’ятати, що конкретний інвестор може запропонувати свою методику, в залежності від специфіки його роботи, проте всі методики мають спільні головні розділи і можуть відрізнятися за логікою подання інформації та більш детальним розкриттям деяких розділів, важливих з точки зору інвестора.
Також, інвестор може оцінювати стан інноваційної розробки за класифікатором IRL (Innovation Readiness Level), який складається з наступних рівнів:
· IRL 1: винахід або команда з ідеєю;
· IRL 2: аналіз комерційних перспектив;
· IRL 3: експериментальне дослідження;
· IRL 4: розробка основних технологій; бізнес-план;
· IRL 5: проектна підтримка конструювання і проектування;
· IRL 6: тестування прототипу системи;
· IRL 7: обмежене виробництво; повністю укомплектована бізнес-команда;
· IRL 8: можливість переходу до повномасштабного виробництва і розповсюдження;
· IRL 9: повністю готовий бізнес з відповідною інфраструктурою і персоналом.
Перших 3 рівні належать до наукової фази, рівні з 4 по 6 – це технологічна фаза, з 7 по 9 є бізнес-фазою. Зрозуміло, що чим вищий рівень інноваційного процесу, тим вищі шанси компанії знайти зацікавленого інвестора.
Головними умовами за яких потенційний інвестор може погодитись на фінансування проекту або стартапу (start up – (починати, запускати), компанія, яка утворюється для реалізації інноваційної ідеї).
1. Насамперед – це актуальна, затребувана місія, тобто проблема, яку стартап спроможній вирішити.
2. Навіть венчурний інвестор не буде вкладати кошти в проекти із занадто високим рівнем ризику. Отже проект повинен гарантувати вирішення поставленого завдання, тобто бути достатньо визначеним, чітким.
3. General Due Diligence – процедура комплексної, поглибленої перевірки об'єкту інвестування, яка здійснюється інвестором та складається з дослідження всіх аспектів діяльності компанії, включаючи юридичні, фінансові питання, менеджмент, кадровий склад, позиціювання компанії на ринку. При цьому перевірка складається з двох блоків. До першого блоку відносяться чинники які впливають на досягнення необхідного, очікуваного від проекту результату, до другого блоку фактори, що негативно впливають на успіх проекту. Головною метою інвестора при здійсненні такого аналізу є створення цілісного портеру стартапу. При цьому увага приділяється не тільки об’єктивним даним, а й суб’єктивним чинникам, таким як психологічна характеристика членів команди, історія їх професійної діяльності, особисті досягнення.
4. Важливим моментом є можливість вільного виходу інвестора з проекту. Це пов’язано з тим, що у разі негативного розвитку подій інвестори, з метою повернення інвестицій, можуть вимагати продажу компанії або її виходу на IPO (Initial Public Offering – процедура первинного публічного розміщення акцій компанії), що для невеликих компаній є доволі проблематичним, оскільки підтримка статусу акціонерного товариства вимагає достатньо суттєвих фінансових витрат.
Досвід вдалих інноваційних проектів свідчить, що при бізнес-плануванні ініціатори стартапу виходили з принципу самоокупності, тобто застосовували обережний підхід з акцентом на кошти, які самостійно заробляє компанія. Важливим позитивним моментом такого підходу є стимул до максимального ефективного використання наявних ресурсів, в тому числі шляхом ретельного планування, а також відсутність ризиків пов’язаних з залученням кредитних коштів. У свою чергу така позиція компанії привертає увагу як інвесторів, так і банківських кредиторів та надає можливість залучати зовнішні фінансові ресурси на вигідних умовах.
У цьому зв’язку, цікавою є інформація щодо структури фінансування інноваційних проектів в Європейських країнах. Так, значну частку серед інвесторів займають бізнес – ангели (71%), венчурний капітал (24%), краудінвестинг – новий, стрімко зростаючий вид фінансування здебільшого за рахунок фізичних осіб (5%).
Розглянемо розповсюджені помилки ініціаторів стартапу, які можуть негативно вплинути на рішення інвесторів щодо фінансування проекту.
· Автори бізнес-плану повинні враховувати в ньому декілька прогнозованих варіантів розвитку проекту. Бізнес-ангели або венчурні фонди, як слід зацікавлені у зростанні компанії, тому занадто стриманий, консервативний прогноз не буде стимулювати їх до вкладання коштів. Проте, на вітчизняному ринку банківського кредитування, консервативний прогноз має більше шансів на погодження.
· Обіцянки авторів бізнес-плану стосовно стовідсоткової доходності капіталу швидше за все будуть скептично сприйняті інвестором, що також буде підставою для сумнівів щодо обґрунтованості фінансового плану та розрахунку ризиків.
· І навпаки, компанія яка збирається зайняти лише 5% певного сегменту ринку буде сприйматися власником капіталу як пасивна та така, що не має потенціалу для росту.
· Інвестори віддають перевагу проектам, які вже реалізують свою продукцію (послуги), а не тільки заявляють, що їх товари або послуги потрібні ринку.
· Якщо у бізнес-плані відсутній аналіз конкурентного середовища, а його автори вважають, що конкурентів просто не має, інвестори здебільшого вважатимуть такий проект фіктивним.
Стандартними розділами бізнес-плану є:
1. Резюме, історія компанії, ініціатори проекту, головні завдання, місія.
2. Характеристика продукції компанії або послуг.
3. Стислий опис технологій (науково-технічних розробок), процесу виробництва (надання послуг) та ризик їх старіння.
4. Аналіз ринкової кон’юнктури, конкурентного середовища та перспектив росту.
5. Маркетинговий аналіз та стратегія, план продажів.
6. Фінансовий аналіз, оцінка грошового обороту та прибутку.
7. Топ-менеджмент, власники, організаційна структура, професійна характеристика, плани щодо найму персоналу.
8. Способи інвестування та шляхи виходу інвесторів з проекту.
9. Оцінка ризиків.
Важливим моментом є мова бізнес-плану, вона повинна бути зрозумілою перш за все для інвестора, адже у більшості випадків він не є фахівцем в сфері технологій. Тому не слід використовувати технічний сленг або захаращувати текст складними науковими реченнями та формулами.
Відносно обсягу бізнес-плану не існує єдиного стандарту, проте на практиці в середньому він складає 30 с., отже бізнес-план не повинен бути дисертацією. Закордонні інвестори взагалі віддають перевагу стислим проектам на 15-20 стор.
Досить важливим моментом, який часто недооцінюється засновниками сатрапів є резюме бізнес-плану. Проте для інвестора цей презентативний розділ є своєрідним індикатором, який вказує на доцільність подальшого вивчення проекту. Резюме повинно мати обсяг не більше двох сторінок та містити головну інформацію щодо інноваційного проекту.
Зауважимо, що не існує єдиного стандарту складання бізнес-плану. Перш за все, такий план потрібен відповідати вимогам того суб’єкта інноваційної діяльності від рішення якого залежить реалізація проекту. Проте не заважаючи на важливість планування та обґрунтування інноваційної ідеї, перш за все слід пам’ятати, що в кінцевому підсумку інвестор оцінює Вашу спроможність реалізувати бізнес-план.5. Моделювання організаційної форми реалізації бізнес-проєкту
Ефективність бізнес-проєкту може бути успішнішою за належної форми організації його реалізації. Ідеальної організаційної структури немає, тому потрібно оцінити різні варіанти організаційної структури реалізації проєкту.
Термін структура організації та її проектування стосується загальної системи структурних елементів організації та зв'язків між ними, які використовують для її керуванням. Структура формується під впливом різних чинників:
Спеціалізація робіт - ступінь, до якого розділене на менші частини загальне завдання організації реалізації бізнес-проєкту.
Структуртація - функційний поділ, поділ за продукцією, поділ за споживачами, поділ за розміщенням.
Звітність - відображення діяльності компанії. Слугує базою для контролю і аналізу.
Повноваження - влада, делегована організацією.
Координація - процес стикування дій різних посад та підрозділів.
Ситуативні чинники - базова технологія, середовище, розмір організації та цикл її існування.
На сьогоднішній день існують чотири базових форми проектування організаціі (компанії), які займаються реалізацією бізнес-проєктів і, відповідно, певна кількість форм, які використовують той чи інший елемент цих базових форм.
Функційна (U-) форма. Функційна форма - це проектування, що грунтується на функційному підході до структуризації. Цей проект названо U-формою (U - unitary унітарний). В організації, що має структуру типу U-форми, працівники та організаційні одиниці об'єднані у великі функційні відділи, такі як відділ маркетингу, виробничий відділ та інші. Для ефективної діяльності організації в цьому випадку потрібна горизонтальна координація, тобто координація роботи відділів, що знаходяться на одному рівні.
За таку інтеграцію та координацію найчастіше відповідає виконавчий директор і менеджери вищого рівня. На рис. 7. 1 показано U-форму стосовно корпоративного рівня невеликої виробничої компанії. За такого проектування жодна з функційних сфер не може існувати без інших. Маркетинг, наприклад, отримує продукцію з виробництва для продажу, а кошти - з фінансового відділу, щоб заплатити за рекламу. Фірми, які використовують U-форму, - WD-40 Company, яка виробляє широковживані мастильні матеріали, та Mcllhenny Company, яка виробляє соус Tabasco.
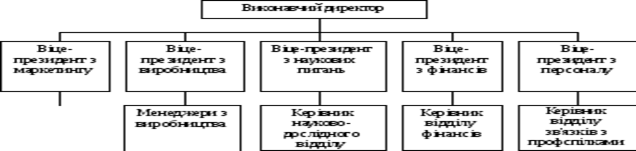
Рис.7. 1. Функційна (U-) форма для виробничої компанії
Проте ця форма має як суттєві переваги, так і недоліки функційної структури. Наприклад, віна дає змогу організації укомплектовувати всі ключові посади функційними спеціалістами й полегшує координацію та інтеграцію. З іншого боку, це також потребує скоріше функційного, а не організаційного акценту, веде до посилення централізації. Як зазначено вище, проект функційної форми найчастіше використовують у виробничих організаціях, оскільки виконавчий директор має змогу особисто контролювати та координувати діяльність цілої фірми. В міру зростання організації такий контроль проводити щораз важче.
Конгломератна (Н-) форма.Іншою базовою формою проектування організації є конгломератна, або Н-форма. Конгломерату форму використовують організації, які утворилися внаслідок об'єднання різних, не пов'язаних між собою підприємств. Отже, проект Н-форми по суті є холдинговою компанією, яка діє за непов'язаної диверсифікації (Н—holding). Цей підхід грунтується на продуктовій формі структури, тобто загальний менеджер незалежно керує кожним підприємством або групою підприємств і відповідає за прибутки чи збитки фірми. Н-форму проектування організації використовує британська фірма PLC. Як показано на рис. 7.2, Pearson займається шістьма видами бізнесу, хоча її періодичні видання та видавництва пов'язані одне з одним, а решта підприємств – не пов'язані.
В організації з Н-формою керівництво корпорації, зазвичай, прогнозує діяльність кожного з підприємств; розподіляє загальні ресурси по компаніях, ухвалює рішення стосовно купівлі та продажу підприємств. Головний недолік організації з проектуванням типу Н-форми - це складність, пов'язана з холдингом різних непов'язаних виробництв, оскільки менеджерам важко поєднувати та інтегрувати різні види діяльності внаслідок великої кількості диверсифікованих операцій. Дослідження свідчать, що багато організацій, які використовують цей підхід, досягай лише середнього або нижче середнього фінансового рівня. Отже, хоча деякі амери- риканські фірми все ще застосовують Н-форму, однак більшість компаній вже відмовилася від неї, замінивши її іншим підходом.

Рис.7.2. Конгломератна Н-форма британської фірми Pearson
Філіальна (М-) форма. Філіальна структура організації використовується організаціями продуктової форми, в яких, на відміну від Н-форми, відділи зв'язані між собою. Філіальна форма, або М-форма (M-multi-divisional), грунтується на багатьох виробництвах, зв'язаних між собою, і які працюють у межах великої організації. Це проектування є результатом стратегії пов'язаної диверсифікації. Деякі види діяльності тут надзвичайно децентралізовані - аж до рівня підрозділів, інші - централізовані на корпоративному рівні. Такий підхід використовує The Limited. Тут кожен підрозділ очолює загальний менеджер, який має автономію в розумних межах. Однак кожний підрозділ повинен узгоджувати свої дії з іншими. Крім The Limited, такий підхід застосовують The Walt Disney Company (розважальні парки, кінотеатри, торговельні заклади) і Hewlet-Packard (комп'ютери, принтери, сканери, медичне електронне обладнання та інша електронна апаратура).
Можливість координації та поділ ресурсів є однією з найбільших переваг проекту М-форми. Відділи маркетингових досліджень The Limited та їхні відділи постачання є централізованими, тобто, покупець може оглянути весь асортимент виробів та придбати проект для мережі The Limited, інші - для Express, а ще інші -для Lerner New York. Головна мета М-форми - мінімізація внутрішньої конкуренції та поглиблення співробітництва між відділами для досягнення вищої ефективності у використанні ресурсів. Дослідження свідчать, що організація, яка використовує М-форму і досягає цього балансу, працює більш ефективно ніж ті організації, що використовують U- та Н-форми.
Матрична форма. Матрична модель є ще одним підходом до організаційного проектування. Вона грунтується на двох поєднаних критеріях структуризації. Основа матричної організаційної структури - група функційних відділів, що займається продуктом, або тимчасові відділи на які покладені обов'язки функційних відділів. Працівники створеної матриці є водночас членами фракційного відділу однієї або кількох проектних груп.
Матричний проєкт показано на рис.7.3. Як бачимо, нагорі організації є функційні одиниці, якими керують віце-президенти з питань інженерії, виробництва, фінансів та маркетингу.
Кожний із менеджерів має декілька підлеглих. По вертикалі організації є певна кількість посад менеджерів проекту. Кожний менеджер є головою проектної групи, що складається з представників функційних підрозділів. Матриця відображає складну структуру субординації - будь-яка особа звітує як функційному керівникові, так і одному або декільком менеджерам проєкту. Кожну проектну групу або команду створюють для окремого проекту або програми.
Наприклад, бізнес-проєкт передбачає налагодити виробництво нового продукту. Для цього, вибирають із кожної функційної ділянки представників груп(відділів), щоб вони працювали над цим проектом як команда, причому вони також зберігають членство в першій функційній групі (відділі). Ford використав цей підхід для створення популярного автомобіля Taurus. Він сформував групу Team Taurus із проектувальників, інженерів, спеціалістів з виробництва, спеціалістів з маркетингу та інших експертів з різних відділів компанії. Робота цієї групи дала змогу випустити дуже популярний автомобіль на ринок щонайменше роком швидше, ніж у разі застосування філіального підходу. Пізніше фірма використала матричний підхід для випуску нової моделі Thunderbird.
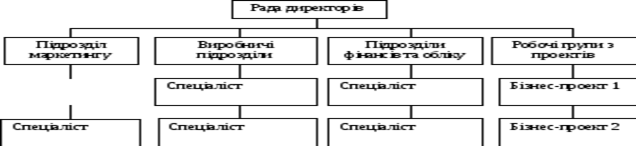
Рис. 7.3. Матрична організація
Матричне проектування має як переваги, так і недоліки. Можна виділити шість головних переваг матричного проектування. По-перше, розширення гнучкості, оскільки групи можна створювати, переукомплектовувати, розпускати в разі потреби. По-друге, ці групи можуть брати активну участь в ухваленні рішень, і члени групи мають вищий рівень мотивації. По-третє, в матричних організаціях працівники мають добру нагоду набувати нових навичок. По-четверте, матричний проект забезпечує підвищення ефективності використання людських ресурсів. По-п'яте, члени групи зберігають членство у своїх функційних одиницях, отже, вони можуть слугувати своєрідним "мостом" між функційними одиницями та групою, розширюючи співробітництво. По-шосте, матричний проект корисний для менеджменту тим, що він дає змогу впроваджувати децентралізацію, тобто поточною діяльністтю займаються призначені менеджери, а вище керівництво може приділити більше уваги перспективному плануванню.
З іншого боку, матричний проєкт має певні недоліки. Службовці можуть розгубитися щодо підпорядкованості, особливо якщо вони водночас звітують і функційному менеджеру, і кільком проектним менеджерам. Ускладнює справу те, що деякі менеджери вбачають у матриці форму анархії, де вони мають необмежену свободу. Інші проблеми пов'язані з динамікою поведінки групи, оскільки група потребує більше часу для ухвалення рішення, в ній може домінувати одна особа, яка занадто часто може йти на компроміс. У матричному проєкті організації необхідно більше часу для координації пов'язаних завдань.
Комбінована форма. Деякі організації використовують проєкт, який є гібридом двох чи більше базових проектів організації. Наприклад, організація, що має п'ять зв'язаних відділів і один незв'язаний, використовує проект, який чимось нагадує і М-форму і Н-форму. Насправді ж, небагато компаній використовують проект у чистому вигляді - більшість мають один головний проект організації як основу керування бізнесом, зберігаючи, однак, достатню гнучкість для того, щоб можна було внести тимчасові чи постійні зміни для досягнення стратегічних цілей. Ford, наприклад, використав матричну форму, щоб спроектувати модель Taurus, проте компанія, в основному, застосовує проектування організації U-форми, маючи тенденцію до зміщення в бік М-форми.
Сьогодні в складному та змінному середовищі появляються нові оригінальні бізнес-проєкти, які потребують нових організаційних форм їх реалізації, а отже менеджмент продовжує есперементувати з різними комбінаціями використання базових елементів організаційних форм, забезпечуючи підвищення ефективності розробленого бізнес-проєкту.
Шрифти
Розмір шрифта
Колір тексту
Колір тла
Кернінг шрифтів
Видимість картинок
Інтервал між літерами
Висота рядка
Виділити посилання
Вирівнювання тексту
Ширина абзацу