Тема 3. Методи формалізації просторово-розподіленої інформації
| Сайт: | Навчально-інформаційний портал НУБіП України |
| Курс: | Візуалізація геопросторових даних ☑️ |
| Книга: | Тема 3. Методи формалізації просторово-розподіленої інформації |
| Надруковано: | Гість-користувач |
| Дата: | субота, 7 березня 2026, 21:57 |
Зміст
- 1. Тема 3. Методи формалізації просторово-розподіленої інформації
- 2. Просторова інформація в ГІС
- 3. Растрове подання просторових даних
- 4. Векторне подання метричних даних. Точкова полігональна структура. DIME-структура.. Структури «дуга-вузол»
- 5. Вибір способу формалізації і перетворення структур даних
- 6. Презентація та додаткові відеоматеріали
1. Тема 3. Методи формалізації просторово-розподіленої інформації
ПЛАН
2. Просторова інформація в ГІС
Просторова (картографічна) інформація є основою інформаційного блока ГІС, тому способи її формалізації є найважливішою складовою частиною технології географічних інформаційних систем.
Просторова інформація ГІС містить метричну частину, що описує позиційні властивості об'єктів, а також пов'язані з нею змістовні (семантичні, тематичні) атрибути, чи просто - «атрибути», як їх прийнято називати в англомовній науковій літературі.
Сучасні технології введення просторових даних у комп'ютер, їх інтерпретації і збереження передбачають поелементний поділ змісту існуючих карт. Для введення, наприклад, топографічної карти необхідно здійснити її поділ на шари («теми») однорідної інформації, що містять дані про рельєф, гідрографічну мережу, населені пункти, дорожну мережу, адміністративні межі та ін. Банки картографічних даних у ГІС, таким чином, містять однорідні шари інформації, що, однак, можуть поєднуватися засобами ГІС один з одним у різному співвідношенні відповідно до вимог розв'язуваних завдань. З урахуванням того, що банк картографічних даних у ГІС може містити сотні шарів однорідної просторової інформації, це відкриває широкі можливості для побудови первинних оригіналів поелементних карт на основі шарів однорідних картографічних даних, що зберігаються в комп'ютері.
Просторові дані вводяться і зберігаються в комп'ютері у формалізованому вигляді. У наш час використовуються два основних способи формалізації просторових даних — растровий і векторний, відповідні двом принципово різним способам опису (моделям) просторових даних. У першому способі просторова інформація співвідноситься з комірками регулярної сітки як з елементамитериторії (растрове подання), у другому — використовується система елементарних графічних об'єктів, положення яких у просторі визначається за допомогою координат (векторне подання). Вибір способу формалізації визначається багатьма факторами, серед яких: характер просторової інформації, джерело одержання даних, специфіка розв'язуваних завдань, ємність вільної комп'ютерної пам'яті, швидкодія комп'ютера і деякі інші.
3. Растрове подання просторових даних
Растровий спосіб формалізації просторових даних має два різновиди — регулярних мереж (grid cells) і власне растровий (raster), що принципово не відрізняються один від одного, оскільки і той і інший базуються на формалізації просторової інформації за комірками (cells) регулярної мережі, що суцільно покриває територію. У кожній комірці цієї мережі інформація відображається одним числом.
Під методом регулярних мереж звичайно розуміють ручний спосіб оцифрування просторових даних шляхом осереднення або генералізації значень елемента, що цифрується, у кожному квадраті сітки — середнього значення висоти земної поверхні, довжини гідрографічної мережі, концентрації забруднювача, переважаючого різновиду ґрунтового покриву і т.п., що історично передував появі автоматичних методів растеризації просторової інформації, але застосовується і сьогодні. Перші зразки реалізації даного методу як одного з методів аналітичного картографування В.Г. Лінник (1990) відносить, посилаючись на роботу У. Тоблера (США), до 1951 року. На сьогодні уявляється доцільним розглядати метод регулярних мереж як спосіб кодування просторової інформації в рамках растрової моделі даних. Відзначимо також, що останнім часом цей спосіб усе рідше згадується в спеціальній літературі у зв'язку з повсюдним переходом на автоматизовані методи створення цифрових растрових карт.
3.1. Загальна характеристика
Растровий спосіб формалізації просторових даних, чи растрова модель просторових даних, у найпростішому випадку полягає в зображенні просторових об'єктів у вигляді мозаїки, що суцільно покриває територію. Ця мозаїка і називається растром. Кожен елемент растра називається чарункою (коміркою) растра або пікселем (від англ. pixel, що є скороченням від picture element — елемент зображення).
Найчастіше використовуються комірки квадратної форми, хоча досить широко відомі комірки трикутної і шестикутної форм. Трикутна мозаїка більш гнучка, ніж чотирикутна, і, в принципі краще підходить для моделювання тривимірних поверхонь. Шестикутна ж мозаїка (з комірками, представленими рівними правильними шестикутниками) приваблива тим, що всі сусідні комірки є еквідистантними, тобто відстань між центрами всіх сусідніх комірок однакова, чого не можна сказати, наприклад, про квадратні і тим більше прямокутні комірки растра.

Види растрових комірок
У растровій моделі просторова інформація кодується у вигляді прямокутної матриці — за рядками і стовпцями, розмір якої відповідає розміру вихідного растра. У зв'язку з цим положення кожного елемента растра в просторі визначається номерами стовпця і рядка, у яких розміщений даний елемент. При растеризації картографічних зображень стовпці звичайно розміщуються в напрямку північ-південь, а рядки — захід-схід. Як початкова комірка (з координатами 0, 0 чи 1, 1) найчастіше використовується комірка, розміщена у верхньому (або нижньому) лівому куті растра.
Шари растрової інформації для бази даних ГІС, можуть бути підготовлені вручну — шляхом кодування інформації для кожної комірки растра і подальшого введення в комп'ютер за допомогою текстового редактора або електронних таблиць. Однак виконання такої роботи можна здійснити практично лише при розмірі растра в кілька десятків чи сотень елементів, що не є характерним для сучасних геоінформаційних систем.
Досвід розв'язання завдань, пов'язаних з оцінкою динаміки речовинних потоків в агроландшафтних системах з використанням ГІС, показує, що в багатьох випадках розмір комірки растра не повинен перевищувати 20x20 м. Неважко підрахувати, що в цьому випадку для ділянки території 10x10 км растр буде мати розмір 500x500 і містити 250 000 комірок. Цифрова ж модель Землі ЕТОР05, створена Національним центром геофізичних даних США (ЕТОР05..., 1988), містить більш ніж 9 млн комірок поверхні розміром 5x5 хвилин за широтою і довготою. Зрозуміло, тут можливі тільки автоматичні способи підготовки растрових моделей просторових даних — за допомогою сканерів, а також комп'ютерної растеризації векторних зображень. Растрову структуру мають також дані дистанційного зондування зі штучних супутників Землі.
Поєднання семантичної і позиційної інформації, що є основним позитивом растрових моделей просторових даних, у той самий час обумовлює один з їх істотних негативів - необхідність великої ємності пам'яті для збереження оцифрованих даних у комп'ютері. Так, стандартний знімок зі штучного супутника Землі США серії Ландсат (Landsat), що охоплює близько 30 000 км кв при номінальному розмірі піксела 30x30 м, складається з 35 млн пікселів (Star, Estes, 1990), що еквівалентно приблизно 35 Мб при записі у форматі 1:1.
3.2. Ієрархічні растрові структури
Растрові структури зручні для відображення ієрархічно організованої географічної інформації. Подання растрової інформації у вигляді кількох внутрішньо пов'язаних рівнів, при якому нижній рівень відповідає вихідному поданню растра, що має розмір NxM елементів, а кожний розміщений вище є узагальненням інформації в т комірках нижчого рівня, називається ієрархічною растровою структурою. Ієрархічні растрові структури іноді називають пірамідальними, або деревоподібними.

Ієрархічна растрова пірамідальна модель
Частковим, однак таким, що досить часто використовується в ГІС, різновидом ієрархічних растрових структур є квадротомічні структури растрових даних, чи квадродерева (quadtree, Q-tree), які відрізняються тим, що в них кожен вищерозміщений рівень є узагальненням інформації строго за чотирма комірками нижчерозміщеного рівня. Завдяки цьому квадродерево має жорстку структуру, що не вимагає додаткового опису. Це — деревоподібний граф, ступінь вершини кожного вузла якого дорівнює 4, тобто розмір комірки кожного вищерозміщеного шару в 4 рази більший, ніж попереднього.

Ієрархічна растрова структура у вигляді квадродерева
У. Тоблер і 3. Чен (Tobler, Chen, 1986) розглянули пірамідальну структуру, що могла б бути корисною при кодуванні даних для всієї поверхні Землі. Одинична вершина на верхньому рівні піраміди (дерева) представляє повну поверхню Землі. На 15-му рівні розмір комірки порівнянний з тим, що одержують від метеосупутників, на 26-му рівні просторова роздільна здатність порівняна з роздільною здатністю аерофотознімків, а на 30-му рівні — це роздільна здатність сантиметрового масштабу. У ГІС ORRMIS, розробленій в США для цілей регіонального планування, виділено шість рівнів ієрархії. На верхньому рівні, призначеному для збереження агрегованих даних масштабу біома чи континенту, розмір комірок 7,5x7,5 хвилин (площа 15606,6 га), на нижньому — розмір комірок, по яких зберігаються висоти поверхні, 10x10 м (площа 0,01 га). Число максимальних за розміром комірок — 140, мінімальних — більше 200 млн.
Ємність пам'яті, необхідна для збереження пірамідальних структур даних, трохи більша, ніж для збереження вихідного зображення. При послідовному подвоєнні сторони комірок при переході від нижчого рівня до вищого (тобто в квадротомічних растрових структурах даних) це збільшення становить близько 30%. Однак воно, безумовно, виправдовується підвищенням інформативності й універсальності бази даних, а також ефективності ряду алгоритмів обробки просторових даних.
3.3. Стиснення растрових даних
Зменшення витрат машинної пам'яті для збереження растрових даних досягається використанням алгоритмів стиснення. Одним із простих і досить ефективних методів стиснення растрових даних є групове кодування (run-length encoding), що використовує просторову автокорельованість даних, особливо чітко виражену на класифікованих картах, тобто на картах контурів або ареалів, у межах яких всі комірки містять однакове значення). Так, у межах даного ґрунтового контуру на ґрунтовій карті, ландшафтного контуру на ландшафтній карті і т.ін. всі комірки растра мають те саме значення, що відповідає, наприклад, номеру даного таксона в легенді відповідної карти.
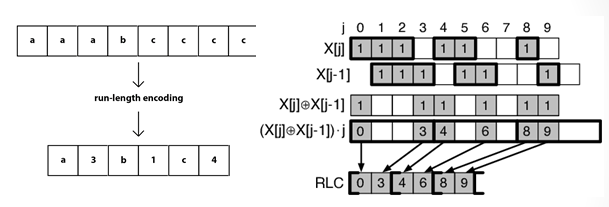
Групове кодування (run-length encoding)
Групове кодування полягає в кодуванні інформації, яка міститься в кожному рядку вихідної матриці за допомогою пар значень, перше з яких являє собою кількість однакових значень кодованого елемента, що йдуть один за одним, друге — значення елемента. У такому випадку матриця, зображена на рис. 4.1 редукується до вигляду:
У тому самому випадку, коли немає необхідності подання даних за рядками, вона зводиться до такого вигляду:
2,2 6,1 2,2 19,1 1,3 7,1 2,3 7,1 1,3 17,1.
Як бачимо, інформація, подана на рис. 4.1, кодується за допомогою 31 чи 20 чисел, замість 64 при записі у форматі 1:1. Таким чином, ємність пам'яті, що займається, в цьому випадку, становитиме 48% і 31% вихідної відповідно.
У тому випадку, коли растрове зображення представлене двома значеннями — 1 і 0, перше з яких відповідає, наприклад, коміркам, які розміщені всередині контуру об'єкта, що відслідковується, друге — поза ним, для стиснення інформації використовується рядковий код (row code), який являє собою послідовність груп з трьох чисел, розділених крапкою з комою. Перше число — це номер рядка, а наступні два — номери комірок у рядку, що маютьненульові значення. У разі наявності в рядку груп комірок з ненульовими значеннями через кому вказуються номери початкової і кінцевої комірок для кожної групи.
Ефективним способом стиснення растрової інформації є використання квадротомічних структур даних. Особливістю квадродерев є те, що вони дозволяють зберігати й обробляти тільки значущі фрагменти растра. Перехід на нижчі рівні в квадродереві здійснюється лише для просторово неоднорідних комірок даного рівня. Якщо комірка є однорідною, вона кодується на даному рівні. Саме це в поєднанні з жорстко заданою архітектонікою даної ієрархічної структури і відсутністю необхідності зберігати інформацію з незначущих фрагментів растра забезпечує значну економію машинної пам'яті. Крім цього, жорстко задана архітектоніка Q-дерева дозволяє здійснювати швидкий доступ до даних.
4. Векторне подання метричних даних. Точкова полігональна структура. DIME-структура.. Структури «дуга-вузол»
Векторне подання метричних даних.
Векторним способом подання просторових даних, або векторною моделлю, називають спосіб формалізації просторових даних, що ґрунтується на використанні набору елементарних графічних об'єктів, або «графічних примітивів».

Графічний примітив
В основу векторної моделі покладено точку (point) — первинний графічний елемент із координатами (х, у), місце розташування якого відоме з довільно заданою точністю. Дві точки з координатами (х1, у1) і (х2, у2) формують другий графічний примітив, лінію (line) — відрізок прямої, що з'єднує ці точки. Замкнута послідовність ліній відокремлює частину поверхні — полігон (polygon), який є третім з основних елементарних графічних об'єктів, або графічних примітивів, на яких базується векторна модель просторових даних.

Точкова полігональна структура
Сукупність цих трьох елементарних графічних об'єктів — точки, лінії та полігону — цілком достатня для опису форми як лінійних, так і просторових картографічних об'єктів, які в цьому випадку кодуються як сукупність координат точок, що апроксимують форму лінійного об'єкта, наприклад, адміністративного кордону, русла ріки і т.п., або контуру (границі) територіального об'єкта, наприклад, території землекористування населеного пункту, басейну ріки і т.п. У базі даних у цьому випадку зберігається пооб'єктна інформація про координати точок введення. У структуру таблиць може бути введена атрибутивна інформація для об'єктів, що цифруються, а також інформація про графічне зображення об'єктів на карті.

Точкова полігональна структура (point polygon structure)
Спосіб векторного подання метричних даних з використанням трьох зазначених вище елементарних графічних об'єктів має назву точкової полігональної структури (Point Polygon Structure) векторних даних. Він належить до категорії нетопологічних векторних структур даних, які часто називають «спагеті».
Цей різновид векторних структур просторових даних відповідає початковому періоду розвитку ГІС-технології, хоча деякі сучасні ГІС-пакети використовують цей формат і далі. Прикладом може бути формат MIF/MID — MapInfo Data Interchange Format — відкритий обмінний формат пакета MapInfо, а також шейп-файли (shapefiles) ГІС-пакетів фірми ESRI.
Основний недолік цього способу формалізації просторових даних полягає у відсутності в запису даних топологічної інформації (інформації про взаємне розміщення об'єктів), що вимагає при введенні метричних даних за допомогою дигітайзера проводити повний обхід кожного полігона. Це призводить до подвійного проходу по спільних для двох суміжних полігонів межах, що обумовлює значне збільшення витрат часу на введення, а також появу двох, що не збігаються через неточності позиціонування дигітайзера, спільних границь суміжних просторових об'єктів, які створюють так звані «паразитні» полігони.
Значного поширення в наш час набули топологічні векторні структури, у яких, крім ідентифікаторів об'єктів і координат, кодується також інформація про взаємне розміщення об'єктів.
DIME-структура
Наприкінці 60-х років XX ст. у Бюро перепису США (US Bureau of the Census) при підготовці до чергового перепису населення було розроблено структуру збереження просторової інформації, яку було названо за першими літерами слів Dual Independent Map Encoding (подвійне незалежне кодування карт) DIME-структурою. Вона належить до топологічних векторних структур даних.
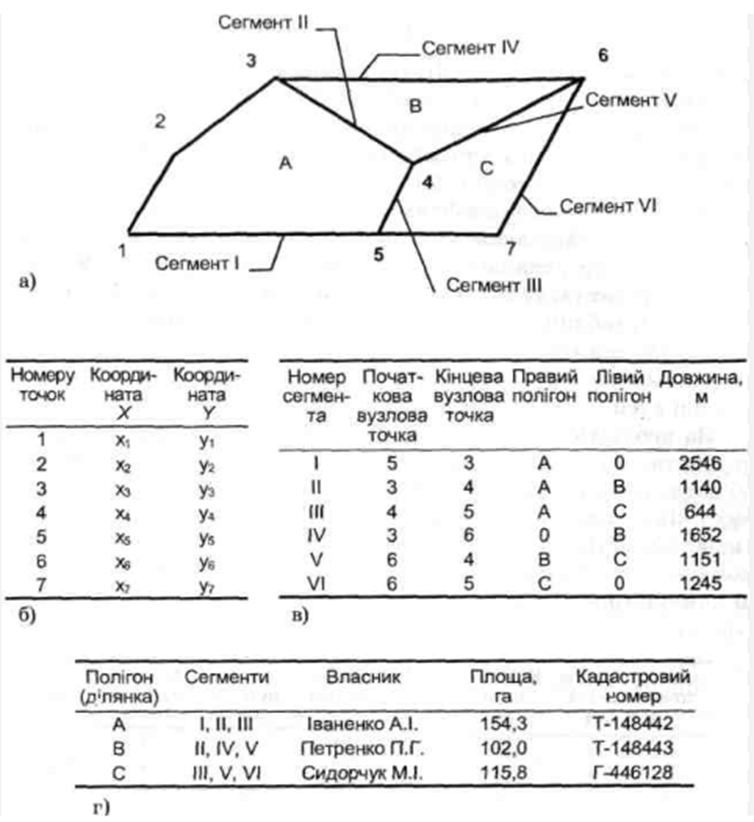
DIME- структура
Основним елементом DIME-структури є дуга (arc) або сегмент (segment) — послідовність ліній, що починається і закінчується вузловими точками. Під вузловою точкою (node) розуміють точку перетину трьох і більш ліній. Хоча сьогодні як вузлова точка або вузол найчастіше розглядається будь-яка початкова або кінцева точка послідовності ліній, що утворює сегмент, або дугу. Так, зокрема, трактується поняття «вузлова точка» у рамках пакета IDRISI.
Введення топологічних характеристик у структуру векторних даних дозволило уникнути основного недоліку точкових полігональних структур — необхідності подвійного обведення спільних меж і пов'язаних з цим похибок. Кожна точка при цьому запам'ятовується тільки один раз у складі якого-небудь сегмента (дуги) і може використовуватися багаторазово — стільки разів, скільки це буде необхідно.
Структури «дуга-вузол»
Подальшим розвитком DIME-структури є векторні топологічні структури типу дуга-вузол (Arc-Node Structure), або лінійно-вузлові структури векторних даних, у яких об'єкт у базі даних структурований ієрархічно, а базовими елементарними графічними об'єктами, крім точки, лінії і полігону є дуга (або сегмент). Опис метричного навантаження карти в базі даних з використанням лінійно-вузлової структури векторних даних, як і в DIME-структурі, складається з трьох наборів даних: 1) таблиці пар координат (х, у) точок введення, що представляють геометрію дуг, 2) таблиці атрибутів дуг і 3) таблиці атрибутів полігонів. Але на відміну від DIME-структури в таблиці атрибутів дуг наводяться тільки початкова (from) і кінцева (to) точки (вузли) кожної дуги. Вказівки на лівий і правий полігони не наводяться. За необхідності в структуру таблиць можуть бути введені атрибути, що характеризують точкові, лінійні або полігональні об'єкти. Це можуть бути, наприклад, характеристики початкових і кінцевих точок введення дуг, назви вулиць (лінійних об'єктів) і їх метричні характеристики, власники земельних ділянок (полігональних об'єктів), їхня площа і унікальні кадастрові номери

Лінійно-вузлові (топологічні) структури векторних даних представлені досить великою кількістю різновидів. Відзначимо модель TIGER (The Topologically Integrated Geographic Encoding and Referencing data format), яку було розроблено в Бюро переписів США для заміни DIME-структури наприкінці 80-х років XX ст., а також DLG-структуру (Digital Line Graph Structure) — стандарт Геологічної служби США (USGS) для пошарового кодування інформації, що міститься на топографічних картах і DLG-Е — Digital Line Graph-Enhanced — розширену версію формату DLG, а також покриття (coverage) – топологічний векторний файл ГІС-пакетів фірми ESRI.
Геореляційна структура
Останніми роками для організації векторних даних у рамках лінійно-вузлової моделі широко використовується реляційна, або геореляційна, структура даних, де метрична та топологічна інформація організована так само, як у лінійно-вузлових структурах, але додаткова (атрибутивна) інформація зберігається в базі даних в окремих реляційних таблицях. Таким чином,геореляційна структура забезпечує однозначну відповідність точкових, лінійних і полігональних об'єктів атрибутивній інформації, яка дозволяє вибирати й аналізувати інформацію, що міститься в базі даних, як за просторовими, так і за атрибутивними критеріями. Просторові й атрибутивні дані, при використанні геореляційної структури записуються в серію таблиць.
Відзначимо також, що в більшості сучасних систем векторної формалізації метричних даних використовуються лінійні сегменти, які складаються із послідовних відрізків прямих ліній. Теоретично при необмеженому зменшенні відстані між точками введення, які обмежують ці відрізки, може бути описана будь-яка крива. Однак на практиці це призводить до надмірного збільшення витрат ручної праці при введенні складних кривих.
Розроблено різні методи апроксимації кривих, які дозволяють не вдаватися до надмірного зменшення кроку дигітизування при введенні навіть дуже складних кривих (границь ґрунтових чи ландшафтних контурів, берегової лінії, русел рік, горизонталей, трас доріг та ін.). Найчастіше з цією метою використовуються аналітичні методи опису відрізків кривих — як дуг окружностей змінного радіуса, або з застосуванням сплайнів.
TIN-модель
Найбільш використовуваною векторною полігональною структурою (моделлю) просторових даних є трикутна нерегулярна мережа (Triangulated Irregular Network), відома під абревіатурою TIN. Вона будується шляхом об'єднання відомих точкових значень у серії трикутників за алгоритмом тріангуляції Делоне. Модель використовується для представлення поверхні у вигляді сукупності суміжних тривимірних (3D) трикутних граней, що не перекриваються.

Лінійна нерегулярна мережа системи нерівнокутних трикутників - TIN
Основний принцип алгоритму тріангуляції Делоне полягає в тому, щоб з наявного набору точок з відомими висотними позначками (значеннями координати Z) побудувати трикутники, які всі разом будуть максимально близькими до рівносторонніх фігур. Досягається це постійним контролем умови, відповідно до якої будь-яке коло, проведене через три вузли в трикутнику, не включатиме ніякого іншого вузла.
Завдяки своїй «нерегулярності» TIN-модель є більш гнучкою порівняно з растровою і дозволяє більш компактно і з меншими похибками описати поверхні з вкладеними формами, такі, як, наприклад, топографічна поверхня. Тому TIN-модель звичайно використовується для побудови цифрових моделей рельєфу, зокрема, у рамках програмних ГІС-пакетів фірми ESRI (ARC/INFO, ArcView GIS, ArcGIS).
Модель розглядає вузли або точки мережі як первинні елементи (Burrough, McDonnel, 1998). Топологічні відношення встановлюються шляхом створення в базі даних для кожної вузлової точки вказівок на сусідні вузли. Простір, що оточує територію, яка моделюється TIN, подається фіктивною вузловою точкою. Це допомагає в описі топології примежових точок і спрощує цю процедуру.
База даних TIN-моделі містить три набори записів: список вузлових точок, список покажчиків і список трикутників. Список (таблиця) вузлових точок містить номери вузлових точок, їхні координати, кількість сусідніх вузлових точок і початкове положення ідентифікаторів цих сусідніх точок у списку покажчиків. Вузлові точки на межі розглянутої області використовують як покажчик якогось фіксованого значення, наприклад — 32000. Список (таблиця) покажчиків для кожної вузлової точки містить номери сусідніх вузлових точок. Список сусідніх вузлів починається від північного напрямку і відповідає ходу годинникової стрілки.
Списки вузлових точок і покажчиків містять всю істотну атрибутивну і топологічну інформацію, тому вони використовуються в багатьох додатках. При деяких додатках, таких, як картографування ухилів або аналітичне затінення схилів, необхідно вміти посилатися безпосередньо на трикутники. Ця процедура виконується з використанням списку трикутників шляхом зв'язування кожного спрямованого ребра мережі з трикутником, розміщеним праворуч. У результаті кожен трикутник асоціюється (зв'язується) із трьома просторово орієнтованими ребрами, описаними в списку покажчиків.
Специфічним методом опису об'єктів є восъмизв'язний код Фрімана. Це набір з восьми цифр (0, 1, 2, 3, 4, 5, 6, 7), кожна з яких кодує один із восьми фіксованих напрямків. Опис форми будь-якої кривої в цьому випадку є послідовністю цифр, що характеризують напрямок на кожному кроці дигітизування.

На закінчення згадаємо про ланцюгове кодування (chain encoding) векторних даних як про спосіб стиснення векторної інформації. Ланцюгове кодування застосовується у випадках, коли відстань між точками введення настільки мала, що приріст координат між суміжними точками виражається малими частками одиниці, як у наведеному нижче прикладі:
(45,4580; 30,7288) (45,4571; 30,7292) (45,4566; 30,7284) (45,4561; 30,7274).
При ланцюговому кодуванні повністю записуються лише координати першої точки. Для всіх же інших вказується приріст координат між поточною точкою і попередньою, виражений в тисячних частках одиниці, із зазначенням знака:
(45,4580; 30,7188) (-09, +04) (-05, -08) (-05, -10).
Таким чином досягається істотне стиснення інформації. Однак можливості застосування даного методу кодування обмежені дуже незначними змінами координат між сусідніми точками введення (не більше 0,0099 (Core Curriculum, 1991)).
5. Вибір способу формалізації і перетворення структур даних
Растрові і векторні структури даних мають свої переваги і недоліки. До переваг растрових структур слід віднести злиття позиційної і семантичної атрибутик просторової інформації в єдиній прямокутній матриці; при цьому відпадає необхідність в особливих засобах збереження й обробки семантики просторових даних (як у векторних структурах), що значно спрощує аналітичні операції з растровими зображеннями, зокрема, оверлейний аналіз. Основними недоліками растрового подання є значна ємність машинної пам'яті, необхідна для збереження растрових даних; висока вартість сканерів, що забезпечують автоматизоване введення інформації; а також недостатньо висока точність позиціонування точкових об'єктів і зображення ліній (особливо похилих), зумовлена генералізацією інформації в межах комірки растра.
Основними перевагами векторного подання є компактність збереження (часто в десятки разів вища, ніж при растровому), висока точність позиціонування точкових об'єктів і зображення ліній. Однак векторні моделі мають складну систему опису топологічної структури даних, унаслідок чого їх обробка вимагає виконання складних геометричних алгоритмів визначення положеннявузлових точок, стикування сегментів (дуг), замикання полігонів та ін. Це значно сповільнює маніпулювання векторними даними, особливо на персональних комп'ютерах з порівняно невеликою швидкодією.
Порівняння переваг і недоліків двох основних структур просторових даних показує, що вони взаємно протилежні один одному — переваги одного способу формалізації є недоліками іншого, і навпаки. Це визначає необхідність застосування в рамках ГІС обох способів і, отже, наявності можливості перетворення (конвертації) однієї структури в іншу, і навпаки (виконання так званих вектор-растрових і растр-векторних перетворень), що в наш час реалізовано у всіх досить потужних ГІС-пакетах. При цьому розв'язання різних завдань доцільно виконувати з використанням того способу формалізації просторових даних, який у даному випадку більш ефективний.
Виходячи з їх переваг і недоліків, векторні структури рекомендується використовувати для збереження феноменологічно-структурованої інформації (ґрунтові і рослинні ареали, ареали використання земель та ін.), для мережного аналізу, у тому числі транспортних і телефонних мереж, а також для підвищення якості відображення при картографуванні лінійних об'єктів, растрові структури — для швидкого і дешевого накладення карт і просторового аналізу, а також моделювання в тих випадках, коли доводиться працювати з поверхнями (наприклад, топографічними) (Burrough, 1986). Дуже ефективним, зокрема для високоякісного картографування, є поєднання векторного і растрового форматів з використанням векторного формату для збереження і побудови ліній, а растрового — для наповнення (розфарбування) площ.
Ідея вектор-растрового перетворення досить проста: точка заміняється коміркою, лінія — послідовністю комірок, територіальний об'єкт (полігон) — сукупністю комірок із заданим розміром. При цьому укладається угода, наприклад, про те, що при перетворенні ліній у растр значущими стають всі комірки, через які проходить лінія, а при перетворенні полігонів — тільки ті з них, у яких межею полігона відтинається значна частина комірки.
Принцип конвертації растрових структур просторових даних у векторні також очевидний: зміст кожної комірки зводиться до точки, положення якої відповідає, наприклад, геометричному центру цієї комірки. Однак на практиці реалізація цього принципу ускладнюється «розмитістю» лінійних об'єктів і меж територіальних, наявністю «шумів», особливо при векторизації даних дистанційного зондування або растрових зображень, отриманих шляхом сканерного введення. У цьому випадку необхідне проведення попередньої обробки растрових зображень з метою «придушення» шумів, «стоншення» лінійних об'єктів і меж територіальних, «скелетизації» зображення.
Слід зазначити також, що існують пропозиції щодо комбінованих растр-векторних подань просторових даних, які поєднують вигоди растрового і векторного подань і не потребують вектор-растрового чи растр-векторного перетворення. До таких комбінованих моделей просторових даних відносять матрично-символьні структури, що є узагальненням квадротомічних структур даних, і растрове представлення, основною логічною одиницею якого є система, яка поєднує кілька рядків сканування і містить елементи векторного і растрового подань.
6. Презентація та додаткові відеоматеріали
Шрифти
Розмір шрифта
Колір тексту
Колір тла
Кернінг шрифтів
Видимість картинок
Інтервал між літерами
Висота рядка
Виділити посилання
Вирівнювання тексту
Ширина абзацу