Практична робота 5. Алгоритми Data Mining: кластеризація
Практична робота 4. Алгоритми Data Mining: кластеризація
Практична робота №4. АЛГОРИТМИ DATA MINING: КЛАСТЕРИЗАЦІЯ
Тема 4. АЛГОРИТМИ DATA MINING: КЛАСТЕРИЗАЦІЯ
Мета роботи: Провести кластерний аналіз
Завдання 1. Здійснити кластерний аналіз
Завдання 3. Одержані результати зобразити графічно
Завдання 4. Зробити висновки
Методичні вказівки.
# install.packages('rattle')
data(wine, package='rattle')
head(wine)У цьому наборі даних ми спостерігаємо склад різних вин. З урахуванням набору спостережень (x1, x2,., Xn), де кожне спостереження є d-мірним реальним вектором, k-середнє кластеризація має на меті розділити n спостережень на (k≤n) S = {S1, S2 ,. , Sk} таким чином, щоб мінімізувати внутрішньокластерну суму квадратів (WCSS). Іншими словами, його мета - знайти:
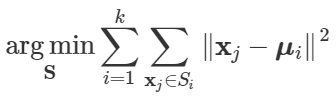
де μi - середнє значення точок Si. Завдання оптимізації кластеризації вирішується за допомогою функції kmeans в R.
wine.stand <- scale(wine[-1]) # To standarize the variables
# K-Means
k.means.fit <- kmeans(wine.stand, 3) # k = 3У k.means.fit містяться всі елементи виводу кластера:
attributes(k.means.fit)# Centroids:
k.means.fit$centers# Clusters:
k.means.fit$cluster# Cluster size:
k.means.fit$sizeФундаментальне питання полягає в тому, як визначити значення параметра k. Якщо ми розглянемо відсоток відхилень, що пояснюється як функція кількості кластерів: слід вибрати декілька кластерів, так що додавання іншого кластера не дає набагато кращого моделювання даних. Точніше, якщо на графіку відсоток відхилень, пояснений кластерами проти кількості кластерів, перші кластери додадуть багато інформації (пояснюють велику дисперсію), але в якийсь момент граничний приріст зменшиться, даючи кут у графік. На цьому етапі вибирається кількість кластерів, отже, «Elbow-критерій».
wssplot <- function(data, nc=15, seed=1234){
wss <- (nrow(data)-1)*sum(apply(data,2,var))
for (i in 2:nc){
set.seed(seed)
wss[i] <- sum(kmeans(data, centers=i)$withinss)}
plot(1:nc, wss, type="b", xlab="Number of Clusters",
ylab="Within groups sum of squares")}
wssplot(wine.stand, nc=6) Бібліотеки, які використовуються для побудови кластерів дозволяють нам представляти (за допомогою PCA) кластерне рішення в 2 виміри:
library(cluster)
clusplot(wine.stand, k.means.fit$cluster, main='2D representation of the Cluster solution',
color=TRUE, shade=TRUE,
labels=2, lines=0)Для того, щоб оцінити продуктивність кластерів, ми створюємо матрицю:
table(wine[,1],k.means.fit$cluster)Ієрархічна кластеризація:
Ієрархічні методи використовують матрицю відстаней як вхід для алгоритму кластеризації. Вибір відповідної метрики буде впливати на форму кластерів, оскільки деякі елементи можуть бути близькими один до одного на одній відстані і далі на іншу.
d <- dist(wine.stand, method = "euclidean") # Euclidean distance matrix.Ми використовуємо евклідову відстань як вхідний сигнал для алгоритму кластеризації (мінімальний критерій відхилення Уорда мінімізує загальну дисперсію кластерів)
H.fit <- hclust(d, method="ward")## The "ward" method has been renamed to "ward.D"; note new "ward.D2"Вихід кластеризації може бути відображений у дендрограмі
plot(H.fit) # display dendogram
groups <- cutree(H.fit, k=3) # cut tree into 5 clusters
# draw dendogram with red borders around the 5 clusters
rect.hclust(H.fit, k=3, border="red") Форма подання: виконана робота надсилається на сайт у форматі Word з прикріпленим файлом R.
Критерії оцінювання: за правильно і вчасно виконану роботу максимальна оцінка - 5балів.
Оцінюються правильність розрахунків і зроблених висновків.
5 балів: Практична робота виконана згідно навчально-методичних вимог за запропонованим завданням у розрізі окремого варіанту.
Матеріал опрацьовано у повному обсязі і викладено правильно і послідовно, немає суттєвих зауважень щодо змісту.
Під час захисту роботи на парі студент формулює висновки за темою дослідження.
4 бали: Практична робота виконана згідно навчально-методичних вимог за запропонованим завданням у розрізі окремого варіанту.
Матеріал опрацьовано у повному обсязі і викладено правильно і послідовно, немає суттєвих зауважень щодо змісту.
Студент формулює висновки з певними неточностями або ті, які не відповідають запропонованій темі.
3 бали: Практична робота виконана згідно навчально-методичних вимог за запропонованим завданням у розрізі окремого варіанту.
Матеріал опрацьовано у повному обсязі і викладено з певними помилками у розрахунках, немає суттєвих зауважень щодо змісту. Неакуратне оформлення.
Студент формулює висновки з певними неточностями або ті, які не відповідають запропонованій темі.
2 бали: Практична робота виконана згідно навчально-методичних вимог за запропонованим завданням у розрізі окремого варіанту.
Матеріал опрацьовано у певному обсязі і викладено з помилками у розрахунках. Неакуратне оформлення.
Студент формулює суперечливі, неправильні висновки або ті, які не відповідають запропонованій темі.
1 бал: Практична робота виконана згідно навчально-методичних вимог за запропонованим завданням у розрізі окремого варіанту.
Матеріал опрацьовано фрагментарно, представлено не у повному обсязі і викладено з помилками у розрахунках. Неакуратне оформлення.
Студент формулює суперечливі, неправильні висновки або ті, які не відповідають запропонованій темі.
Шрифти
Розмір шрифта
Колір тексту
Колір тла