Тема 2. Алгоритми Data Mining: класифікація і регресія
Класифікація – розподіл елементів даних в один з декількох наперед визначених класів елементів.
Класифікація є найбільш поширеною моделлю для ССС. З її допомогою виявляються ознаки, що характеризують групу, до якої належить той чи інший об'єкт. Це робиться за допомогою аналізу вже класифікованих об'єктів і формулювання деякого набору правил.
Класифікація допоможе виявити характеристики об’єктів і створити модель, що здатна передбачати, до якого класу відноситься досліджуваний об’єкт. Один раз визначений ефективний класифікатор використовують для класифікації нових даних у вже існуючі класи й в цьому випадку він здобуває характер прогнозу і може бути використаний для прийняття рішення.
В загальному випадку кількість класів в задачах класифікації може бути більше двох. Наприклад, в задачі розпізнавання образу цифр таких класів може бути 10 (за кількістю цифр в десятковій системі числення). В такій задачі об'єктом класифікації буде матриця пікселів, що представляє образ розпізнаваної цифри. Тут характеристикою аналізованого об'єкта буде колір кожного піксела.
В класифікації часто застосовують визначення значення одного з параметрів об'єкта на підставі значень інших параметрів. Такий параметр називають залежною змінною, а параметри, що залучені до його визначення - незалежними змінними.
В розглянутих прикладах незалежними змінними є:
- Зарплата, вік, кількість дітей тощо.
- Частота певних слів.
- Значення кольору пікселів матриці.
Залежними змінними в цих же прикладах є:
- Кредитоспроможність клієнта (можливі значення цієї змінної "так" або "ні").
- Тип повідомлення (можливі значення цієї змінної "spam" або " mail ").
- Цифра образу (можливі значення цієї змінної 0, 1,..., 9).
У розглянутих прикладах залежна змінна приймає значення з кінцевої множини значень: {так, ні}, {spam, mail}, {0, 1,..., 9}. Якщо значеннями незалежних і залежної змінних є дійсні числа, то завдання називається регресією. Прикладом завдання регресії може бути визначення суми кредиту, яка може бути видана банком клієнту.
Задача класифікації і регресії вирішується в два етапи. На першому етапі формується навчальна вибірка. Вона містить об'єкти, для яких відомо значення як незалежних, так і залежних змінних. В описаних раніше прикладах такими навчальними вибірками можуть бути :
- Інформація про клієнтів, яким раніше видавалися кредити на різні суми та інформація про їх погашення.
- Повідомлення, які позначено вручну як спам або як лист.
- Матриці образів цифр, що було розпізнано раніше.
На підставі навчальної вибірки будується модель для визначення значення залежної змінної. Її часто називають функцією класифікації або регресії. Для отримання максимально точної функції до навчальної вибірки пред'являються такі основні вимоги:
- Кількість об'єктів, що містить вибірка, має бути достатньо великою. Чим більше об'єктів, тим точніше буде функція класифікації або регресії, що побудована на їх основі.
- Вибірка повинна містити об'єкти, що представляють всі можливі класи в разі класифікації або всю область значень у разі регресії.
- Для кожного класу в задачі класифікації чи кожного інтервалу області значень в задачі регресії вибірка повинна містити достатню кількість об'єктів.
На другому етапі побудовану модель застосовують до нових об'єктів з невизначеним значенням залежної змінної.
Основні проблеми, з якими стикаються при вирішенні задач класифікації і регресії, - це незадовільна якість вихідних даних, в яких зустрічаються як помилкові дані, так і пропущені значення, різні типи атрибутів - числові і категорійні, різна значимість атрибутів, а також проблеми overfitting і underfitting.
- Суть overfitting полягає в тому, що класифікаційна функція, яка дуже точно відтворює дані навчальної вибірки, адаптується до даних, помилок та аномальних значень, що в них зустрічаються і намагається їх інтерпретувати як частину внутрішньої структури даних. Очевидно, що надалі така модель буде працювати некоректно з іншими даними, де характер помилок буде дещо іншим.
- Терміном underfitting позначають ситуацію, коли при перевірці класифікатора на навчальній множині спостерігається значна кількість помилок. Це означає, що особливих закономірностей в даних не було виявлено і або їх немає взагалі, або необхідно вибрати інший метод їх виявлення.
Підходи класифікації:
- імовірнісна класифікація (probabilistic classification),
- класифікація з використанням дерев рішень (decision tree classifier),
- лінійний дискримінантний аналіз (linear discriminant analysis),
- метод опорних векторів (support vector machines).
До імовірнісної класифікації віднесено Байєсівську класифікацію та класифікацію методом k-найближчих сусідів.
- Байєсівська класифікація використовує формулу Байєса для визначення класу, до якого належить об’єкт, як класу з максимальною апостеріорною вірогідністю. Проста Байєсівська класифікація (Naive Bayes classifier) ґрунтується на припущенні, що всі змінні статистично незалежні між собою, і покликана спростити обчислення в порівнянні з повною Байєсівською класифікацією.
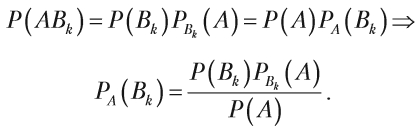
- Класифікація методом k-найближчих сусідів (k-nearest neighbors classifier, KNN classifier) полягає у визначенні класу, до якого належить найбільше найближчих сусідів об’єкта, клас якого визначається, і вважається, що новий об’єкт також належить до цього класу.
Найближчі сусіди визначаються, переважно, за допомогою обчислення відстані між точками у просторі за формулою Евкліда, хоча також можливі інші метрики. Число k позначає кількість найближчих сусідів, які використовуються для класифікації.
- Лінійний дискримінантний аналіз використовується для пошуку лінійної комбінації ознак, яка найкращим чином розділяє об’єкти на класи, або, іншими словами, полягає у знаходженні такого вектора, після проекції на який об’єкти можна розподілити між класами з максимальною сепарацією (максимальним розділенням).
- Як критерій розділення під час аналізу використовується лінійний дискримінант Фішера.
- Метод опорних векторів (SVM) ґрунтується на ідеї, що найкращим способом розмежування точок в m-мірному просторі є m-1 гіперплощина, рівновіддалена від точок, які належать різним класам.
- Основним завданням методу є пошук серед усіх можливих площин такої, яка рівновіддалена від крайніх об’єктів кожного з класів, і такі об’єкти називаються опорними векторами.
Труднощі класифікації і регресії
- Погана якість вихідних даних: помилки, пропуски.
- Різні типи атрибутів.
- Різна значимість атрибутів.
- Overfitting: функція "занадто добре“ адаптується до даних, помилки інтерпретує як частина структури
- Underfitting: велика кількість помилок на навчальній множині, закономірність не виявляються.
2. Регресія в Data Mining
Регресією називають апроксимацію даних з врахуванням їх статистичних параметрів. Таке завдання постає при обробці даних, отриманих в результаті вимірювань процесів або фізичних явищ. Завданням регресійного аналізу є підбір математичних формул, які найкращим чином можуть описати заданий набір.
Математична постановка задачі регресії полягає в наступному. Залежність величини певної властивості об’єкту Y від іншої змінної властивості або параметра Х зареєстровано на множині точок множиною значень. В кожній точці зареєстровані значення відображені з випадковою похибкою. За сукупністю значень потрібно підібрати таку функцію, яка б з мінімальною похибкою відображала зареєстровані дані.
Передумови кореляційно-регресійного аналізу
- Чітке уявлення про причинно-наслідкові зв’язки між досліджуваними ознаками
- Достатня варіація досліджуваних ознак
- Якісна однорідність досліджуваних сукупностей
- Досить велике число спостережень
- Випадковість і незалежність одиниць сукупності одна від одної.
- Досліджувані ознаки повинні мати кількісний (числовий) вираз
Види регресії називаються за типом апроксимуючих функцій: поліноміальна, експоненціальна, логарифмічна.
- Прості (парні) зв’язки:
у = а0 + а1х – лінійний.
- Нелінійні :
у = а0 + а1х + а2х2 – парабола 2-го порядку.
у = а0 +а1 / х – гіпербола.
у = а0 ха1 – степенева функція.
у = а0 а1х – показникові функція.
у = а1 lnx +а0 – логарифмічна.
- Множинні зв’язки:
у = ао +а1х1+а2х2 +… +аnхn – лінійний.
у = ао +а1х12 + а2х22 + … + аnхn2 – нелінійний.
у = ао х1а1х2а2 – нелінійна виробнича функція Кобба-Дугласа.
у = аох1а1х2а2… хmam – загальна виробнича функція Кобба-Дугласа.
Вибірку даних, найчастіше, представляють у вигляді масиву, що складається з пар чисел (xi , yi). Тому, виникає завдання апроксимації дискретної залежності y (x) безперервною функцією f (x). Функція f (x), залежно від специфіки завдання, може відповідати різним вимогам:
- f (x) повинна проходити через точки (xi , yi) , тобто f (хi ) = уi , i = 1 ... n. В цьому випадку говорять про інтерполяцію даних функцією f (х) між точками хi, або екстраполяції за межами інтервалу, що містить всі хi.
- f (х) повинна наближати експериментальну залежність y (xi), враховуючи, що дані (xi, yi) отримано з деякою погрішністю, що виражає шумову компоненту вимірювань. При цьому функція f (х), за допомогою того чи іншого алгоритму, зменшує похибку, що присутня в даних (xi, yi). Такого типу задачі називають фільтрацією.
- f (х) повинна певним чином (наприклад, у вигляді певної аналітичної залежності) наближати y (xi), не обов'язково проходячи через точки (xi, yi). Таку постановку завдання регресії в багатьох випадках можна назвати згладжуванням функції.
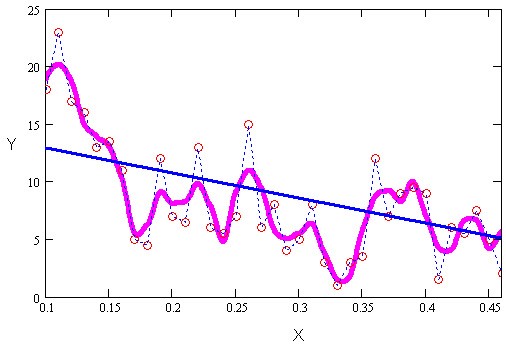
На рисунку проілюстровано різні види побудови апроксимуючої залежності f (х). Тут, вихідні дані позначено точками, інтерполяція - пунктиром, фільтрація - жирною гладкою кривою, а лінійна регресія (згладжування) - похилою прямою лінією.
Базовими функціями для оцінки параметрів регресійної моделі є функція lm() (застосовують для одержання оцінок коефіцієнтів лінійної моделі методом найменших квадратів) та функція glm() (застосовують для отримання оцінок параметрів узагальнених лінійних моделей).
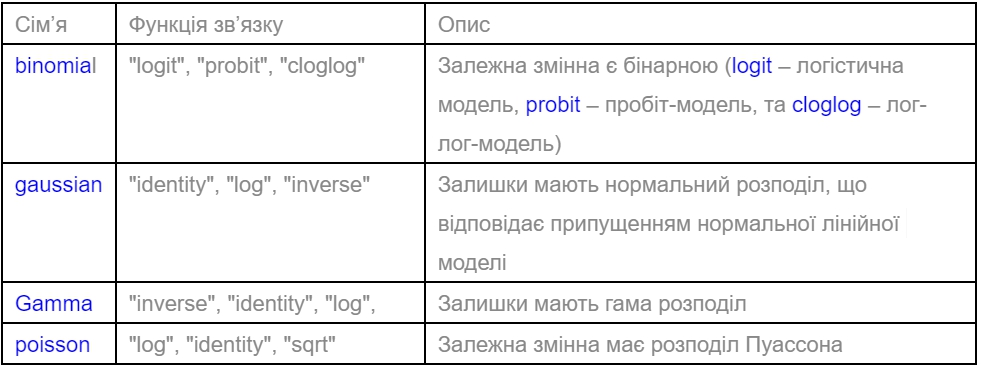
Одним з основних аргументів даних функцій є аргумент formula, який визначає вигляд рівняння регресії, параметри якої мають бути оцінені. Для функції glm() основним аргументом також є аргумент family, який визначає конкретний тип розподілу експоненціальної сім’ї, що мають залишки, та тип функцію зв’язку – link.
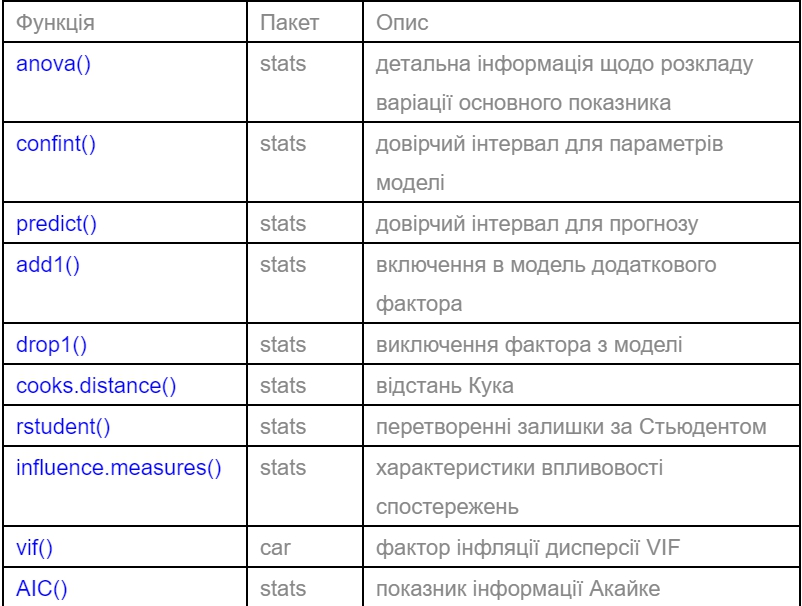
Функції повертають об’єкти, що є списками з цілою низкою полів, що визначають різні характеристики моделі, зокрема поле сoefficients визначає значення оцінених параметрів, residuals – залишки моделі, а поле fitted.values – розрахункові значення моделі. Крім того, для даних об’єктів наявні різні методи, що дозволяють модифікувати модель, визначати різні характеристики адекватності, перевіряти припущення моделі, тощо.
Для зручного представлення результатів оцінювання параметрів можна використати функцію summary(), що фактично є методом класу lm.
Шрифти
Розмір шрифта
Колір тексту
Колір тла
Кернінг шрифтів
Видимість картинок
Інтервал між літерами
Висота рядка
Виділити посилання
Вирівнювання тексту
Ширина абзацу
