L №1_4
Тема роботи: Алгоритми і технології обчислення інтегралів
Мета роботи: навчитись обчислювати інтеграли з допомогою засобів MATLAB
Завдання на роботу
1) Провести інтегрування з накопиченням (крок інтегрування дорівнює 0,5) для інтеграла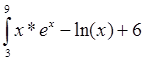 
2) Обчислити значення інтеграла (інтегрування з накопиченням) від функції представленої у вигляді вектора коренів полінома:
Р(х) = х5+8x4+31x3+80x2+94x+20
3) Обчислити за допомогою методу трапеції (крок інтегрування дорівнює 1) значення інтеграла
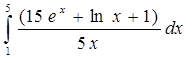
4) Під інтегральна функція має вигляд: f(x) = -е х + 8х 4 + 3 ctg х + 1.
Обчислити методом Сімпсона значення інтеграла від f (x) з точністю 10-5. межі інтегрування [1; 10].
5) Обчислити методом парабол значення подвійного інтеграла від функції
z = ln (x) + ln.
Межі інтегрування по 1 змінної [1, 5], а по зовнішньої змінної [2; 4].
6) З допомогою аналітичного методу знайти значення невизначеного інтегралу
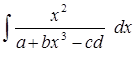
7) З допомогою аналітичного методу обрахувати значення визначеного інтегралу
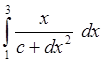
8) Обчислити інтеграл
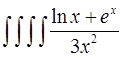
Методичні вказівки (теоретична частина)
- назву та мету роботи;
- наведені приклади;
- програму завдання написану в MathСad ;
- висновки по роботі з аналізом операторів та розроблених програм.
- Максимальний бал (15) студент отримує, якщо вчасно зробить та ЗАХИСТИТЬ роботу впродовж двох тижнів після виконання згідно графіку навчання.
- При не виконанні будь якого з елементів робота вважається невиконаною.
- Лабораторні роботи можуть виконуватись студентом самостійно, в разі наявності відповідного програмного забезпечення згідно варіанту наданого в завданнях.
- В разі невчасного захисту роботи максимальна можлива оцінка 10 балів.
Шрифти
Розмір шрифта
Колір тексту
Колір тла
Кернінг шрифтів
Видимість картинок
Інтервал між літерами
Висота рядка
Виділити посилання
Text Alignment
Paragraph Width