Тема 2. Ідеалізація об’єкта при створенні комп’ютерної моделі. Ідеалізація форми й геометричних параметрів конструкції.

Ідеалізація геометричних параметрів - призначення основних розмірів, які можуть дещо відрізнятися від реальних з метою надання можливої регулярності для скорочення обсягу вихідної інформації та зручності аналізу результатів. У разі прийняття стержневої або пластинчастої схеми відбувається заміна стержнів на «дротову» систему, а пластин — на площинну, яка не має поперечних розмірів. Тут також можливі відступи, допустимість яких визначає інженер: прийняті осі стержнів і пластин можуть не збігатися з їх нейтральними площинами, різні конструктивні включення (наприклад, консолі) можуть бути проігноровані та ін.

Після того, як обрана та частина об’єкта, що фігуруватиме в розрахунку, починається ідеалізація її геометричного образу - геометричне моделювання. У процесі геометричного моделювання вирішується питання про можливу ідеалізацію об’єкта щодо надання йому властивостей регулярності або симетрії [2], хоча сам об’єкт, можливо, і не є строго регулярним, а умови симетрії можуть бути певною мірою порушені.

Основними геометричними схемами елементів конструкцій є: стержень, плита, оболонка, масивне тіло (рис. 2.2).

Стержень — тіло, довжина якого набагато більша від розмірів перерізу, тобто l > h, b.

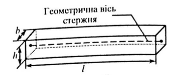
Рис. 2.1 Загальний вигляд стержня

Переважна робота матеріалу в стержні - це розтяг або стиск в осьовому напрямку (особливість представляє деформація кручення). Для фізико-математичної моделі стержня характерним є те, що основні розрахункові рівняння записуються щодо однієї незалежної змінної - координати z. Їх рішення становить так звану одновимірну задачу.

Рис. 2.2 Деформація стержневого елемента

Поперечний переріз — переріз, що лежить у площині, ортогональній геометричній осі.

Пластина – тіло, товщина якого набагато менша від довжини й висоти, тобто δ < b,l.

Природно викривлена пластина (криволінійна до завантаження) називається оболонкою.

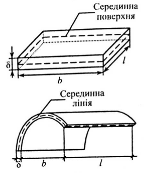
Рис. 2.3 Загальний вигляд пластини і оболонки

Матеріал пластин і оболонок працює в більш складних умовах, ніж у стержня, наприклад, на розтяг - стиск він буде працювати в двох взаємно перпендикулярних напрямках. Математична модель пластин і оболонок, як правило, буде складатися з рівнянь, що залежать від двох аргументів: х та у. Тому така задача відноситься до класу двовимірних задач.

Рис. 2.4 Деформування пластини

Масивне тіло – тіло, у якого всі розміри порівнянні, тобто h-b-l.

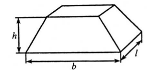
Рис. 2.5 Загальний вигляд масивного тіла

Зважаючи на відсутність будь-якого переважного напрямку в тілі функції, що описують його деформування, будуть істотно залежати від трьох незалежних аргументів х, у, z, тому задача є тривимірною.

Геометрично ці елементи відрізняються один від одного лише співвідношенням характерних розмірів, але з механічної точки зору їх деформування є настільки специфічним, що вимагає отримання своїх рівнянь і залежностей, які складають математичну модель цих елементів.

Стержневі елементів в залежності від їх призначення і виду деформування (рис. 2.6) поділяються на:
- Балки (стержні або бруси, які в основному працюють на згин);
- Стійки або колони (стержневі елементи, що сприймають вертикальні стискаючі сили);
- Розкоси (похилі елементи, що сприймають вертикальні стискаючі сили);
- Вали (стержень, що передає обертальний рух, наприклад, від двигуна до верстата).

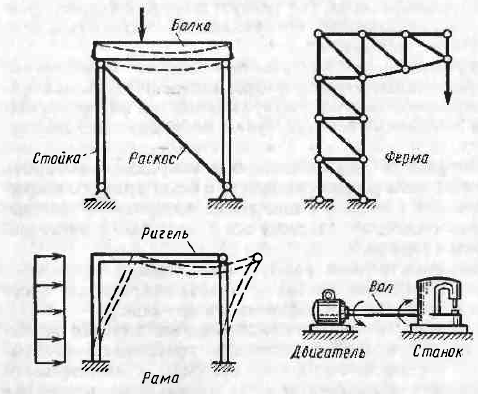
Рис. 2.6 Види стержневих конструкцій

Конструкцію, що складається із сполучених згинальних стержнів, називають рамою. Якщо ж завдяки шарнірному з'єднанню стержнів всі вони працюють тільки на розтяг або стиск (від навантаження, прикладеного у вузлах), то конструкцію називають фермою.

Посилання на додаткове відео стосовно розглянутої теми - тема https://fex.net/uk/s/mycmon5