Лекція 4. Електричні кола однофазного синусоїдного струму

Індуктивний елемент – це елемент електричного кола з двома виводами, в якому відбувається запасання магнітної енергії (енергії магнітного поля), пов’язане з протіканням у колі електричного струму. При цьому вважається, що в такому елементі відсутні втрати електричної енергії та запасання електричної енергії (енергії електричного поля).

Кількісною мірою індуктивного елемента є індуктивність L. Нагадаємо, що термін «індуктивність» зазвичай використовують не тільки як характеристику, але як і назву самого індуктивного елемента.

Як вже нами було встановлено, при проходженні струму крізь індуктивний елемент (індуктивність) навколо останнього утворюється магнітне поле, яке графічно відображається магнітними силовими лініями, що огинають провідники зі струмом і завжди замкнені (див. рис. 4.11).

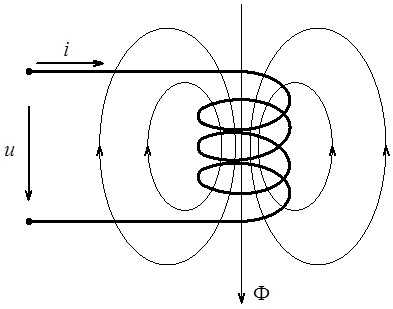
Рис. 4.11. Графічне відображення картини магнітного поля навколо індуктивного елемента

 

Нагадаємо, що магнітне поле характеризується напруженістю (Н) та індукцією (В), які є векторними величинами і відрізняються коефіцієнтом, що зветься магнітною проникністю. Зазвичай магнітна проникність позначається як m, а для вакууму - m₀.

Магнітне поле утворює магнітний потік (Ф) – скалярну величину, що кількісно характеризує поширення магнітного поля крізь визначену поверхню.

Напруженість магнітного поля (як вже було зазначено в розділі 1) вимірюється в «амперах на метр» (А/м), індукція – у тесла (Тл), магнітний потік – у веберах (Вб).

З витками котушки індуктивності зціплені відповідні магнітні потоки, тобто з поверхнею, що утворюється контуром кожного витка котушки, пов’язана визначена напруженість (індукція) її магнітного поля. Ці магнітні потоки, звичайно, неоднакові для різних витків котушки, адже витки котушки в загальному випадку не можуть бути однаковими (число ліній магнітного поля, яке зціплене з окремими витками, неоднакове). Загальний магнітний потік, що зціплений з котушкою індуктивності (потокозчеплення) визначається як алгебраїчна сума магнітних потоків, зціплених з окремими витками цієї котушки, тобто:

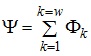                                                (4.8)

Зважаючи на те, що за умови відсутності феромагнітних тіл згідно закону повного струму напруженість магнітного поля пропорційна струму, матимемо:

                                                     (4.9)

Відповідно до (4.9) величина індуктивності визначається як:

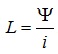                                                       (4.10)

Як вже було відмічено, індуктивність вимірюється у генрі (Гн):

.

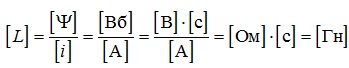Зв'язок між струмом, що протікає індуктивним елементом, та напругою на його полюсах встановлюється на підставі закону електромагнітної індукції: при зміненні магнітного потоку, зціпленого з контуром, в останньому наводиться ЕРС, величина якої дорівнює швидкості змінення цього потоку у часі, та направлена так, щоб викликаний цією ЕРС струм перешкоджав зміненню потоку, який цей струм наводить.

Тобто, згідно закону електромагнітної індукції, коли струм, протікаючи у додатному напрямку, зростає 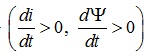, ЕРС повинна мати полярність, яка при відсутності зовнішнього джерела утворила б струм, спрямований назустріч струму i, який саме цю ЕРС і збуджує (завдяки якому ця ЕРС і виникає). Такій полярності відповідає (за домовленістю) додатний напрямок напруги на індуктивному елементі. Таким чином:

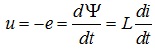                                    (4.11)

З (4.11) за величиною напруги на індуктивному елементі можна визначити струм, який крізь цей елемент протікає, а саме:

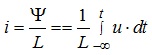                                    (4.12)

У співвідношенні (4.12) нижня межа інтегрування t = -∞ означає необхідність підсумовування всіх попередніх змінень напруги на індуктивному елементі до моменту часу t, тобто визначає необхідність врахування передісторії змінень величини u. При цьому зазвичай приймається:

u = 0 за умови, що t = -∞                          (4.13)

З урахуванням (4.13) співвідношення (4.12) можна подати як:

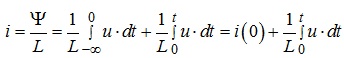         (4.14)

Тобто, відповідно до (4.14) величина струму, що протікає крізь індуктивний елемент у момент часу t визначається як сума двох доданків, один з яких характеризує значення струму у момент часу (t = 0), тобто у початковий момент часу, а другий – всі змінення значення струму від початкового до поточного моменту часу. Значення струму крізь елемент у початковий момент часу при розв’язанні задач зазвичай називають початковими умовами.

Зазначимо, що графічне зображення залежності струму (напруги) від часу часто називають епюрами струму (напруги). Важливо відмітити, що потокозчеплення та струм неперервні, тобто не можуть змінюватися стрибком, адже лише в цьому випадку величина  є величиною кінцевою. Математично вказані умови можна записати як:

.

Енергія, що може запасатися індуктивністю (накопичуватися в індуктивному елементі) визначається як:

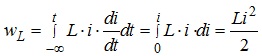              (4.15)

При виводі співвідношення (4.15) прийнято, що при t = -∞ величина струму, який протікає крізь індуктивний елемент, дорівнює нулю. Величина енергії, що накопичується в індуктивності, звичайно, не може мати від’ємного значення, що й підтверджується співвідношенням (4.15). 

Припустимо, що включеною до електричного кола індуктивністю протікає синусоїдний струм, миттєве значення якого визначається як:

.

При цьому на виводах індуктивності виникає ЕРС:

,

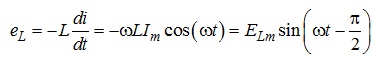де  - амплітудне значення цієї ЕРС.

 

Зважаючи на те, що:

,

співвідношення для миттєвого значення напруги на виводах індуктивності матиме вигляд:

,

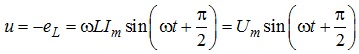де.

Зрозуміло, що для діючих значень напруги та струму, відповідно, матимемо співвідношення:

,

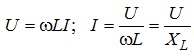де  - індуктивний опір.

 

Миттєва потужність електричного струму, що пов’язана з індуктивністю, характеризує швидкість перетворення електричної енергії джерела живлення в енергію магнітного поля.

Вказана миттєва потужність визначається як:

.

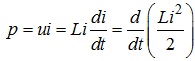З останнього співвідношення видно, що за умови співпадіння знаків u та i (в процесі змінення цих величин) величина потужності додатна, що відповідає запасанню енергії індуктивним елементом, тоді як за умови не співпадіння знаків u та i потужність матиме від’ємне значення (від’ємна потужність), що відповідає віддаванню (попередньо накопиченої) енергії індуктивним елементом у зовнішнє (по відношенню до цієї індуктивності) електричне коло.

За умови, що напруга та струм змінюються за синусоїдним законом, матимемо:

.

На рис. 4.13 показані часові залежності струму, напруги, миттєвої потужності та ЕРС, пов’язані з індуктивним елементом.

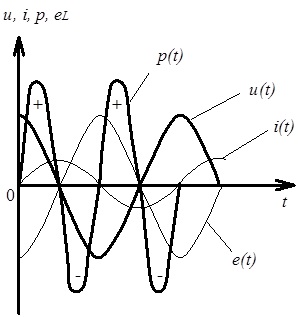
Рис. 4.13. Часові залежності струму, напруги, потужності та ЕРС в електричному колі синусоїдного струму з індуктивністю

 

З рис. 4.13 видно, що в електричному колі з індуктивністю відбувається виключно періодичний обмін енергією між генератором і магнітним полем відповідно до зростання та спадання енергії магнітного поля, яка визначається як:

.

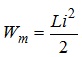При вказаному обміні енергії не відбуваються її перетворення в механічну або теплову енергію.

Отже середня за період активна потужність в електричному колі з індуктивністю дорівнює нулю. За міру швидкості обміну енергії в електричному колі приймають максимальне значення миттєвої потужності, яка зветься реактивною потужністю і визначається як

.

Ще раз підкреслимо, що реактивна потужність (як в індуктивності, так і в інших елементах електричного кола змінного струму) не пов’язане з перетворенням електричної енергії в енергію інших видів, а отже і не пов’язана з виконанням якоїсь корисної роботи.

Реактивна потужність характеризує виключно процеси обміну електричної енергії між окремими елементами відповідного електричного кола. На рис. 4.14 наведена векторна діаграма, яка характеризує зсув фаз між струмом, що протікає індуктивністю, та напругою й ЕРС на виводах цього елемента.

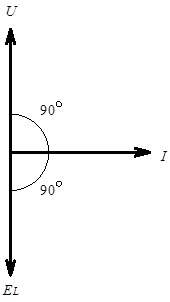
Рис. 4.14. Векторна діаграма, яка характеризує зсув фаз між струмом, що протікає індуктивністю, та напругою і ЕРС на її виводах

 

З рис. 4.14 видно, що синусоїдний струм, який протікає індуктивністю, напругою й ЕРС на виводах цієї індуктивності взаємно ортогональні.