Лекція 4. Електричні кола однофазного синусоїдного струму
4. Електричні кола синусоїдного струму з паралельним з’єднанням елементів
4.1. Загальні характеристики електричного кола з паралельним з’єднанням окремих віток
Вважатимемо, що на вході електричного кола, представленого на рис. 4.34, діє синусоїдна напруга
![]() .
.
При цьому у вітках електричного кола протікатимуть струми
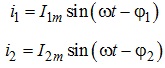
Амплітудні значення струмів І1т, І2т в кожній вітці, відповідні величини зсуву фаз φ1, φ2 та повні опори Z1,Z2 цих віток визначаються аналогічно наведеному вище, а саме:
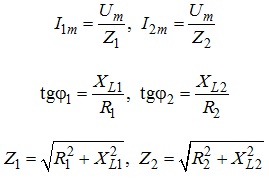
Під час розрахунку електричних кіл з паралельним з’єднанням окремих елементів (віток) доцільно користуватися категоріями провідності Y цих елементів (віток). Нагадаємо, що величина провідності елемента електричного кола зворотна до величини його опору. Це положення справедливе для опорів як активних, так і для реактивних та повних. Отже для електричного кола, що розглядається, матимемо:
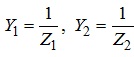 .
.
Амплітудні значення струмів у вітках електричного кола у термінах провідності запишуться як:
![]()
В нерозгалуженій частині електричного кола струм відповідно до першого закону Кірхгофа дорівнюватиме
![]() .
.
Побудуємо векторну діаграму для напруги та визначених значень струмів у вітках електричного кола (див. рис. 4.35).
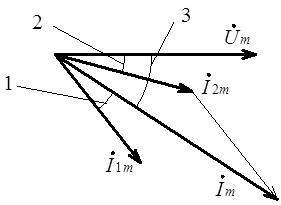
Рис. 4.35. Векторна діаграма напруги та струмів в електричному колі з
паралельним з’єднанням двох віток ![]()
З наведеної векторної
діаграми видно, що струм Im у нерозгалуженій частині електричного кола, є сумою (векторною)
струмів I1m, I2m. Величину цього струму можна розрахувати, використовуючи
відому теорему косинусів для трикутника, утвореного векторами ![]() .
.
Таким чином, для амплітудного значення струму у нерозгалуженій частині електричного кола матимемо:
![]() .
.
Кут зсуву фази струму у нерозгалуженій частині кола, що розглядається, також легко встановити з наведеної на рис. 4.35 векторної діаграми, а саме:
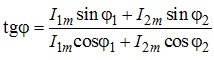 .
.
Наведений алгоритм розрахунку струмів в електричному колі з паралельним з’єднанням віток (елементів) стає надто громіздким при збільшенні кількості віток. Спрощення алгоритму можна отримати за умови введення (за аналогією з аналізом послідовного з’єднання елементів) категорій активної та реактивної складової струмів (а отже й активних та реактивних провідностей). З цією метою розкладемо струми, що протікають в електричному колі на дві ортогональні складові, а саме: на активну складову Іа, спрямовану вздовж осі абсцис, та реактивну складову Ір, спрямовану вздовж осі ординат. За таких умов кожен зі струмів електричного кола дорівнюватиме векторній сумі відповідних складових, одна з яких відображає активну складову струму, а друга – реактивну. Відповідна векторна діаграма подана на рис. 4.36.
Згідно наведеної векторної діаграми для вітки 1:
- активна складова струму
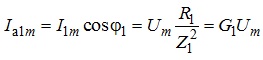 ;
;
- реактивна складова струму
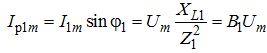 ;
;
де
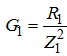 - активна
провідність вітки 1;
- активна
провідність вітки 1;
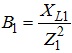 - реактивна
провідність вітки 1.
- реактивна
провідність вітки 1.
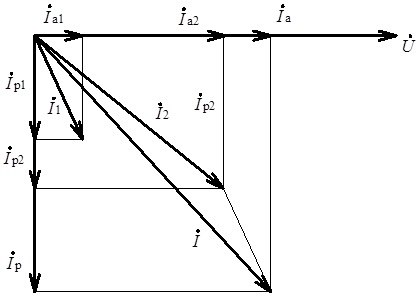
Рис. 4.36. Векторна діаграма представлених активною та реактивною складовими струмів електричного кола з паралельним з’єднанням віток
Знову ж таки на підставі наведеної діаграми для вітки 2:
- активна складова струму
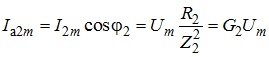 ;
;
- реактивна складова струму
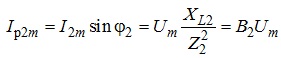 ,
,
де
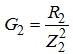 - активна
провідність вітки 2;
- активна
провідність вітки 2;
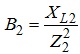 - реактивна
провідність вітки 2.
- реактивна
провідність вітки 2.
За таких умов відповідно до наведеної векторної діаграми струми першої та другої вітки електричного кола відповідно визначаються як:
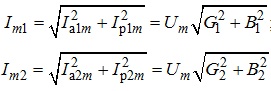 ,
,
де
![]() - повна провідність
першої вітки;
- повна провідність
першої вітки;
![]() - повна провідність
другої вітки.
- повна провідність
другої вітки.
З наведених формул, якими визначають повні провідності віток електричного кола, видно, що активна, реактивна та повна провідності пов’язані між собою як сторони прямокутного трикутника. Такий трикутник зветься трикутником провідностей (див. рис. 4.37). На підставі наведених співвідношень амплітудне значення струму в електричному колі до точки розгалуження (до відповідного вузла) та активну й реактивну складові цього струму можна подати як:
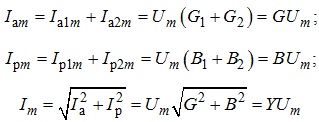
де
![]() - активна складова
загальної провідності обох віток;
- активна складова
загальної провідності обох віток;
![]() - реактивна складова
загальної провідності обох віток;
- реактивна складова
загальної провідності обох віток;
![]() - повна провідність
обох віток електричного кола;
- повна провідність
обох віток електричного кола;
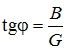 - тангенс кута між
повною провідністю та її активної складової.
- тангенс кута між
повною провідністю та її активної складової.
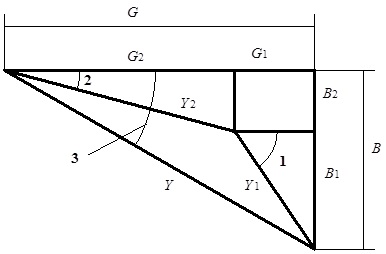
Рис. 4.37. Трикутник провідностей для електричного кола з двома
паралельними вітками ![]()
Активна, реактивна та повна потужність в електричному колі, що розглядається, визначаються як:
- активна потужність
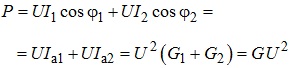
- реактивна потужність
![]() ;
;
- повна потужність
![]() .
.
За умови наявності у колі паралельних віток, одна (або більше) з яких містить ємнісний елемент, задача розв’язуватиметься аналогічно з урахуванням того, що реактивна складова ємнісної провідності від’ємна. При цьому може статися ситуація, за якої реактивні складові віток з індуктивностями дорівнюватимуть реактивним складовим віток з ємностями, а отже реактивна складова з’єднання таких віток дорівнюватиме нулю. Такий режим електричного кола зветься резонансом струмів і характеризується мінімальною провідністю з’єднання віток, а отже й мінімальним струмом у нерозгалуженій частині кола.
Шрифти
Розмір шрифта
Колір тексту
Колір тла
Кернінг шрифтів
Видимість картинок
Інтервал між літерами
Висота рядка
Виділити посилання
Вирівнювання тексту
Ширина абзацу
