Тема 7. Наукова компонента матричного бізнес-проектування

Балансові моделі широко використовують в економічних дослідженнях, аналізі, проєктуванні. Ці моделі будуються на підставі балансового методу, тобто узгодженні матеріальних, трудових і фінансових ресурсів. Якщо описувати економічну систему загалом, то під балансовою моделлю мають на увазі систему рівнянь, кожне з яких виражає балансові співвідношення між виробництвом окремими економічними об’єктами обсягів продукції й сукупною потребою в цій продукції. За такого підходу розглядувана економічна система складається з об’єктів, кожен з яких випускає певний продукт, частина якого споживається ним же та іншими об’єктами системи, а решта виводиться за межі системи як її кінцева продукція. Якщо замість поняття «продукт» увести більш загальне поняття «ресурс», то під балансовою моделлю розуміють систему рівнянь, котрі задовольняють вимоги відповідності щодо наявності ресурсу та його використання. Можна також розглядати приклади балансової відповідності, як-от: відповідність наявної робочої сили й кількості робочих місць, платоспроможного попиту населення та продукції (товарів і послуг) тощо.

Розгляньмо деякі відомі види балансових моделей:

-         часткові матеріальні, трудові й фінансові баланси стосовно до національної економіки чи окремих галузей (регіонів);

-         міжгалузеві баланси;

-         матричні бізнес-плани підприємств і фірм.

Балансові моделі на підставі звітних балансів характеризують наявні пропорції, де ресурсна частина завжди дорівнює витратній. Для виявлення диспропорцій використовують балансові моделі, в котрих фактичні ресурси узгоджувались би не тільки з їх фактичним споживанням, а й з потребою в них. Зазначимо, що балансові моделі не містять якогось механізму порівняння окремих варіантів економічних рішень (як це має місце, наприклад, у разі вибору одного з альтернативних варіантів бізнес-проекту) і не передбачують взаємозаміни різних видів ресурсів, що не дозволяє здійснити вибір оптимального варіанта розвитку економічної системи. Власне, це й визначає деяку обмеженість балансових моделей і балансового методу загалом.

Основу інформаційного забезпечення балансових моделей в економіці становить матриця коефіцієнтів витрат ресурсів за конкретними напрямами їхнього використання. Наприклад, у моделі міжгалузевого балансу таку роль відіграє так звана технологічна матриця — таблиця міжгалузевого балансу, що складається з коефіцієнтів (нормативів) прямих витрат на виробництво одиниці продукції в натуральному вираженні. З багатьох причин вихідні дані реальних господарюючих об’єктів не можуть бути використані в балансових моделях безпосередньо, тому підготовка інформації до введення в модель є досить складною проблемою. Так, для побудови моделі міжгалузевого балансу використовується специфічне поняття чистої (чи технологічної) галузі, що поєднує все виробництво певного (агрегованого) продукту незалежно від адміністративної підпорядкованості й форм власності підприємств і фірм. Перехід від господарських галузей до чистих галузей вимагає спеціального перерахунку реальних даних господарських об’єктів, наприклад, агрегування галузей, вилучення внутрішньогалузевого обігу тощо.

Балансові моделі будуються як числові матриці — прямокутні таблиці чисел. У зв’язку з цим балансові моделі належать до типу матричних економіко-математичних моделей. У матричних моделях балансовий метод дістає чітке математичне вираження. Отже, матричну структуру мають міжгалузевий і міжрегіональний баланси виробництва та розподілу продукції окремих регіонів, бізнес-планів підприємств і фірм тощо. Попри специфіку цих моделей їх об’єднує не лише спільний формальний (математичний) апарат побудови та єдиний алгоритм обчислень, а й аналогічність низки економічних характеристик. Це дає змогу розглядати структуру, зміст і основні залежності матричних моделей на прикладі міжгалузевого балансу та розподілу продукції в національній економіці. Даний баланс відображає виробництво та розподіл суспільного продукту в галузевому розрізі, міжгалузевих виробничих зв’язків, використання матеріальних і трудових ресурсів, створення й розподіл національного доходу.

Принципова схема міжгалузевого балансу (МГБ) виробництва й розподілу суспільного продукту у вартісному вираженні наведена в таблиці 7.1. У підґрунтя цієї схеми покладено поділ сукупного продукту на дві частини: проміжний і кінцевий продукт; уся національна економіка  подана тут як сукупність галузей (чисті галузі). Кожна з цих галузей фігурує в балансі як виробник і як споживач. Розгляньмо схему МГБ в розрізі його блоків, що мають різний економічний зміст, — їх заведено називати квадрантами балансу (на схемі квадранти позначені римськими цифрами).

Таблиця 7.1

ПРИНЦИПОВА СХЕМА МІЖГАЛУЗЕВОГО БАЛАНСУ (МГБ)

Галузі-виробники	Галузі-споживачі					Кінцевий продукт	Валовий продукт
	1	2	3	…	n
1	х11	х12	х13	…	х1n	Y1	X1
2	х21	х22	х23	…	х2n	Y2	X2
3	х31	х32	х33	…	х3n	Y3	X3
. . .	. . .	. . .	. . .	І . .	. . .	ІІ	. . .
n	хn1	хn2	хn3	…	хnn	Yn	Xn
Амортизація	C1	C2	C3	…	Cn	IV
Оплата праці	v1	v2	v3	III	vn
Чистий дохід	m1	m2	m3	…	mn
Валовий продукт	X1	X2	X3	…	Xn

Економіко-математична модель міжгалузевого балансу. Основу інформаційного забезпечення моделі міжгалузевого балансу становить технологічна матриця, що містить коефіцієнти прямих матеріальних витрат на виробництво одиниці продукції. Ця матриця є базою економіко-математичної моделі міжгалузевого балансу.
Коефіцієнти прямих і повних матеріальних витрат. Здійснюючи аналіз моделі міжгалузевого балансу, потрібно розглянути основні властивості матриці коефіцієнтів прямих матеріальних витрат А. Ці коефіцієнти за визначенням є невід’ємними, отже, матриця А в цілому є невід’ємною: А ? 0. Процес відтворення не можна було б здійснити, якщо б для власного відтворення в галузі витрачався більший обсяг продукту, ніж створювався. Звідси очевидно, що діагональні елементи матриці А менші ніж одиниця: aii <1, i = 1, ..., n.
Обчислювальні аспекти розв’язування задач на підставі моделі МГБ.

Галузі-виробники	Галузі-споживачі			Кінцева продукція	Валова продукція
	1	2	3
1	232,6	51,6	291,8	200,0	775,3
2	155,1	255,0	0,0	100,0	510,1
3	232,6	51,0	145,9	300,0	729,6
Умовно чиста продукція	155,0	153,1	291,9	600,0
Валова продукція	775,3	510,1	729,6		2015,0

Перший квадрант МГБ — це таблиця міжгалузевих потоків. Показники, що містяться на перетині рядків і стовпців, є обсягами міжгалузевих потоків продукції xij, i та j — відповідно номери галузей виробників і споживачів. Перший квадрант за формою є квадратною матрицею n-го порядку, сума всіх елементів якої дорівнює річному засобу відтворення амортизації засобів виробництва у матеріальній сфері.

У другому квадранті подана кінцева продукція всіх галузей матеріального виробництва, де під кінцевою продукцією мається на увазі продукція, що виходить зі сфери виробництва в кінцеве використання (на споживання та накопичення). У табл. 8.1 цей розділ подано в узагальненому вигляді як один стовпчик величин Yі,; у розгорнутій схемі балансу кінцевий продукт кожної галузі можна подати диференційовано за напрямами використання: на особисте споживання населення, суспільне споживання, на накопичення, покриття збитків, експорт тощо.

Третій квадрант МГБ також характеризує національний дохід, але з боку його вартісного складу — як суму чистої продукції й амортизації; чисту продукцію тлумачать як суму оплати праці та чистого доходу галузей. Обсяг амортизації (Cj) та чистої продукції (vj + mj) деякої галузі називають умовно чистою продукцією цієї галузі й позначають у подальшому через Zj.

Четвертий квадрант відбиває розподіл і використання національного доходу. В результаті перерозподілу створеного національного доходу утворюються скінченні доходи населення, підприємств, держави.

Дані четвертого квадранта важливі для відображення в міжгалузевій моделі балансу доходів і витрат населення, джерел фінансування капіталовкладень, поточних витрат невиробничої сфери, для аналізу загальної структури доходів за групами споживачів. Загалом МГБ у межах єдиної моделі об’єднує баланси галузей матеріального виробництва, баланс сукупного суспільного продукту, баланс національного доходу, баланс доходів і витрат населення.

Якщо, як показано в табл. 7.1, позначити валовий продукт j-ї галузі літерою Xj, то можна записати два співвідношення, що відбивають сутність МГБ та є підґрунтям його економіко-математичної моделі.

По-перше, розглядаючи схему балансу по стовпчиках, можна зробити висновок, що сума матеріальних витрат будь-якої галузі-споживача та її умовно чистий продукт дорівнює валовій продукції цієї галузі:

Xj 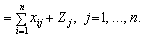  (7.1)

По-друге, розглядаючи МГБ по рядках для кожної галузі-виробника, бачимо, що валова продукція будь-якої галузі дорівнює сумі матеріальних витрат галузей, які споживають її продукцію, і кінцевої продукції даної галузі:

Xi     (7.2)

Підсумовуючи за j систему рівнянь (7.1), дістаємо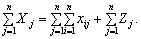 

Аналогічно, підсумовуючи за i систему рівнянь (7.2), дістаємо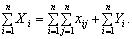 

Звідси легко помітити, що 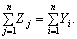 (7.3)

Це рівняння показує, що в міжгалузевому балансі виконується принцип еквівалентності матеріального та вартісного складу національного доходу.

 

Припускається гіпотеза, згідно з якою для виробництва одиниці продукції в j-й галузі необхідна певна кількість витрат проміжної продукції і-ї галузі, що становить aij, і ця величина не залежить від обсягів виробництва в j-й галузі та є досить стабільною величиною в часі. Величини aij називають коефіцієнтами прямих матеріальних витрат та обчислюють таким чином:

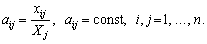 (7.4)

Коефіцієнти прямих матеріальних витрат показують, яку кількість продукції і-ї галузі необхідно витратити, якщо враховувати лише прямі витрати, для виробництва одиниці продукції j-ї галузі. З урахуванням формули (7.4) систему рівнянь балансу (8.2) можна записати у вигляді

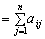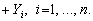Хі      Хі   (7.5)

Якщо ввести до розгляду матрицю коефіцієнтів прямих матеріальних витрат А = (аij), вектор-стовпчик валової продукції X та вектор-стовпчик кінцевої продукції Y:

то система рівнянь (8.5) у матричній формі матиме вигляд

X = AX + Y . (7.6)

Систему рівнянь (7.5), чи у матричній формі (7.6), називають економіко-математичною моделлю міжгалузевого балансу (моделлю Леонтьєва, моделлю «витрати — випуск»). За допомогою цієї моделі можна виконати три варіанти обчислень:

-         задаючи в моделі обсяги валової продукції кожної галузі (Хi), можна визначити обсяги кінцевої продукції кожної галузі(Yi):

Y = (E – A)X, (7.7)

де Е — одинична матриця n-го порядку;

-         задаючи обсяги кінцевої продукції всіх галузей (Yi), можна визначити обсяги валової продукції кожної галузі (Хi):

X = (E – A)–1Y; (7.8)

-         для низки галузей задаючи обсяги валової продукції, а для решти — обсяги кінцевої продукції, можна відшукати величини кінцевої та валової продукції всіх галузей.

У формулах (7.7) та (7.8) Е позначає одиничну матрицю n-го порядку, а (Е – А)–1 — матрицю, обернену до матриці (Е – А).

Якщо визначник матриці (Е – А) не дорівнює нулеві, тобто ця матриця не вироджена, тоді існує матриця, обернена до неї. Позначимо цю матрицю через В:

B = (Е – А)–1. (7.9)

Систему рівнянь у матричній формі (8.8) можна записати:

X = BY . (7.10)

Елементи матриці В позначатимемо через bij , тоді з матричного рівняння (8.10) для будь-якої і-ї галузі можна отримати співвідношення:

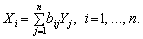 (7.11)

Із співвідношення (7.11) випливає, що валова продукція постає як зважена сума обсягів кінцевої продукції, ваговими коефіцієнтами тут є bіj, котрі показують, скільки всього необхідно виробити валової продукції і-ї галузі для випуску у сферу кінцевого використання одиниці продукції j-ї галузі. На відміну від коефіцієнтів прямих витрат aij , коефіцієнти bіj називають коефіцієнтами повних матеріальних витрат, і вони включають у себе як прямі, так і опосередковані витрати всіх порядків. Якщо прямі витрати відбивають кількість засобів виробництва, використаних безпосередньо на виготовлення певних обсягів даного продукту, то опосередковані стосуються попередніх стадій виробництва і входять у виробництво продукції не прямо, а через інші (проміжні) засоби виробництва.

Коефіцієнти повних матеріальних витрат bij показують, який обсяг продукції j-ї галузі необхідно виробити, щоб з урахуванням прямих і опосередкованих витрат цієї продукції отримати одиницю кінцевої продукції j-ї галузі.

Коефіцієнти повних матеріальних витрат можна застосовувати, коли необхідно визначити, як вплинуть на валовий випуск певної галузі деякі зміни щодо обсягів випуску кінцевої продукції всіх галузей:

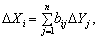 (7.12)

де DXi та DYj — зміни (прирости) обсягів валової й кінцевої продукції відповідно.

 

Система рівнянь міжгалузевого балансу відображає реальні економічні процеси, в котрих сенс можуть мати лише невід’ємні значення валових випусків; таким чином, вектор валової продукції складається з невід’ємних компонентів вектора Х, який є невід’ємним вектором: X > 0. Постає питання, за яких умов економічна система здатна забезпечити невід’ємний кінцевий випуск у всіх галузях? Відповідь на це питання пов’язана з поняттям продуктивності матриці коефіцієнтів прямих матеріальних витрат.

Означення. Називатимемо невід’ємну матрицю А продуктивною, якщо існує такий невід’ємний вектор Х, що

X > AX. (7.13)

Очевидно, що умова (7.13) означає існування невід’ємного вектора кінцевої продукції Y > 0 для моделі міжгалузевого балансу (7.6).

Щоб матриця коефіцієнтів прямих матеріальних витрат А була продуктивною, необхідно і достатньо, аби виконувалася одна з перелічених нижче умов:

-         матриця (Е – А ) має бути невід’ємно оберненою, тобто повинна існувати обернена матриця (Е – А) –1 ? 0;

-         матричний ряд 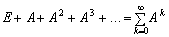  має збігатися, Ak ® 0, k ® ?, а його сума дорівнює оберненій матриці (Е – А)–1;

-         найбільший за модулем l розв’язок (власне значення) характеристичного рівняння 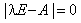  має бути строго меншим від одиниці;

-         усі головні мінори матриці (Е – А), тобто визначники матриць, що утворені елементами перших рядків і перших стовпчиків цієї матриці порядку від 1 до n, мають бути додатними.

Більш простою, але лише достатньою ознакою продуктивності матриці А є обмеження на величину її норми, тобто на величину найбільшої із суми елементів матриці А в кожному стовпчику. Якщо норма матриці А строго менша від одиниці, то ця матриця є продуктивною. Наголосимо, що дана умова є лише достатньою, і матриця А може виявитися продуктивною й у разі, якщо її норма буде більшою за одиницю.

Найбільший за модулем корінь характеристичного рівняння, наведеного в третій умові продуктивності матриці А (позначимо його через l*), може слугувати за оцінку загального рівня коефіцієнтів прямих матеріальних витрат, а отже, величина (1 – l*) характеризує залишок після витрат, тобто продуктивність. Чим більшим є (1 – l*), тим більшими є можливості досягнення інших цілей, окрім поточного виробничого процесу. Іншими словами, чим вищим є загальний рівень коефіцієнтів матриці А, тим більшим — максимальне за модулем власне значення (l* ) і нижчим — рівень продуктивності, і навпаки, чим нижчий загальний рівень коефіцієнтів матриці А, тим меншим є максимальне по модулю власне значення (l* ) і вищою продуктивність.

Проаналізуймо матрицю коефіцієнтів повних матеріальних витрат, тобто матрицю В = (Е – А)–1. Елемент цієї матриці bijпоказує, скільки всього необхідно виробити продукції і-ї галузі, щоб одержати одиницю кінцевої продукції j-ї галузі.

Дамо інше означення коефіцієнта повних матеріальних витрат з огляду на те, що окрім прямих витрат існують опосередковані витрати тієї чи іншої продукції для виробництва продукції даної галузі. Розгляньмо для прикладу формування витрат електроенергії на випуск стального прокату, обмежуючись технологічним ланцюжком «руда—чавун—сталь—прокат». Витрати електроенергії для отримання прокату зі сталі називатимемо прямими витратами, ті самі витрати для отримання сталі з чавуну — опосередненими витратами 1-го порядку, а витрати електроенергії для отримання чавуну з руди — опосередкованими витратами електроенергії на випуск сталевого прокату 2-го порядку тощо. Отже, можна дати таке означення:

Коефіцієнтом квазіповних матеріальних витрат cij називають суму прямих і опосередкованих витрат продукції і-ї галузі для виробництва одиниці продукції j-ї галузі через проміжні продукти на всіх попередніх стадіях виробництва. Якщо коефіцієнти опосередкованих матеріальних витрат k-го порядку позначати через  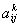, то має місце формула

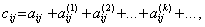 (7.14)

a якщо ввести до розгляду матрицю коефіцієнтів квазіповних матеріальних витрат C = (cij) та матриці коефіцієнтів опосередкованих матеріальних витрат різних порядків 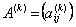 , то поелементну формулу (7.14) можна подати в матричній формі:

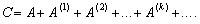 (7.15)

З огляду на змістовну суть коефіцієнтів опосередкованих матеріальних витрат можна записати такі математичні співвідношення:

за використання котрих матрична формула (7.15) набирає вигляду

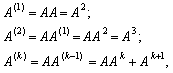 (7.16)

Якщо матриця коефіцієнтів прямих матеріальних витрат А є продуктивною, то з другої умови продуктивності існує матриця В = (Е – А)–1, яка є сумою збіжного матричного ряду:

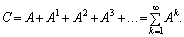 (7.17)

Порівнюючи вирази (7.16) та (7.17), дістанемо:

В = Е + С,

або в поелементному записі: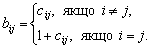 

Це визначає економічний сенс, що пояснює відмінність між коефіцієнтами (елементами) матриць В та С: на відміну від коефіцієнтів матриці С, що враховують лише витрати на виробництво продукції, коефіцієнти матриці В включають у себе, окрім витрат, також одиницю кінцевої продукції, котра виходить за сферу виробництва.

 

Основний обсяг обчислень за моделлю МГБ пов’язаний з обчисленнями матриці коефіцієнтів повних матеріальних витрат В. Якщо матриця коефіцієнтів прямих матеріальних витрат А задана та є продуктивною, то матрицю В можна обчислювати за допомогою формул обернення матриць, що розглядаються в курсі матричної алгебри, або наближеним способом, використовуючи розклад у матричний ряд (7.17).

Розглянемо перший спосіб знаходження матриці В. Знаходимо матрицю (Е – А), а потім, застосовуючи один із прямих методів пошуку обернених невироджених матриць, обчислюємо матрицю (Е – А)–1. Одним із широковживаних методів обернення матриць є метод Жордана. Використовують також метод, що ґрунтується на застосуванні формули

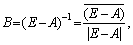 (7.18)

де в чисельнику — матриця, приєднана до матриці (Е – А), елементи котрої є алгебраїчними доповненнями для елементів транспонованої матриці (Е – А)?, а в знаменнику — визначник матриці (Е – А). Алгебраїчні доповнення, у свою чергу, для елементів з індексами і та j дістають множенням співмножника 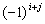  на мінор, що отримується після викреслювання з матриці А і-го рядка й j-го стовпчика.

Згідно з другим способом обчислення матриці коефіцієнтів повних матеріальних витрат використовують формулу (7.17). Обов’язковою умовою коректності цих обчислень є умова щодо продуктивності матриці А, а, здійснюючи обчислення, обмежуються врахуванням опосередкованих матеріальних витрат до певного порядку (наприклад 3-го порядку). Тут використовується процедура множення квадратних матриць з їхнім наступним додаванням, а коефіцієнти повних матеріальних витрат отримуються з деяким наближенням (із заниженням).

Приклад Для тригалузевої економічної системи задані матриця коефіцієнтів прямих матеріальних витрат і вектор кінцевої продукції:

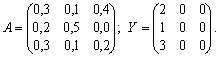
Необхідно обчислити коефіцієнти повних матеріальних витрат і вектор валової продукції, а також заповнити схему міжгалузевого матеріального балансу.

Розв’язання.

1. Визначимо матрицю коефіцієнтів повних матеріальних витрат згідно з другим (наближеним) способом, ураховуючи опосереднені матеріальні витрати до 2-го порядку включно. Запишемо матрицю коефіцієнтів опосередкованих витрат 1-го порядку: 

матрицю коефіцієнтів опосередкованих витрат 2-го порядку:

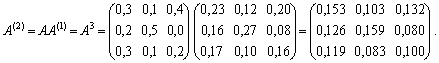
Отже, матриця коефіцієнтів повних матеріальних витрат наближено дорівнюватиме: 

2. Обчислимо матрицю коефіцієнтів повних матеріальних витрат за допомогою формул обернення невироджених матриць (перший спосіб):

а) знаходимо матрицю (Е – А): 

б) обчислимо визначник цієї матриці: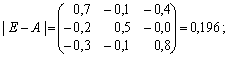 

в) транспонуємо матрицю (Е – А):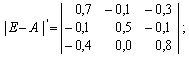 

г) знайдемо алгебраїчні доповнення для елементів матриці 

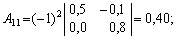
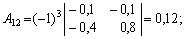
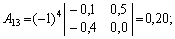
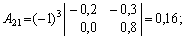
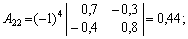
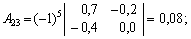
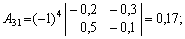
Отже, приєднана до матриці (Е – А) матриця має вигляд: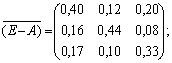 

д) використовуючи формулу (7.18), знаходимо матрицю коефіцієнтів повних матеріальних витрат: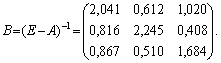 

Як зазначалося, елементи матриці В, що обчислені згідно з першим способом, є дещо більшими, ніж відповідні елементи матриці, обчисленої згідно з другим (наближеним) способом.

3. Знаходимо обсяги валової продукції трьох галузей (вектор Х), використовуючи формулу (7.10):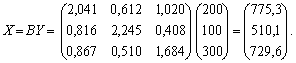 

4. Для обчислення елементів першого квадранта матеріального міжгалузевого балансу скористаємося формулою, що випливає з (7.4), тобто xij = aijXj, i, j = 1, …, n.

Для отримання елементів першого квадранта необхідно елементи першого стовпчика матриці А перемножити на величину X1 = 775,3, елементи другого стовпчика матриці А — на X2 = 510,1; елементи третього стовпчика матриці А — на X3 = 729,6.

Складові третього квадранта (умовно чиста продукція) знаходять з урахуванням формули (7.1) як різницю між обсягами валової продукції та сумами елементів відповідних стовпчиків відшуканого першого квадранта.

Четвертий квадрант у наведеному прикладі складається лише з одного показника й слугує, зокрема, для контролю правильності обчислень: сума елементів другого квадранта повинна (у вартісному матеріальному балансі) збігатися із сумою елементів третього квадранта.