Тема 5. Алгоритмічні (імітаційні) і рейтингові моделі бізнес-проєктування

Метод статистичного моделювання (чи метод Монте-Карло) — це спосіб дослідження невизначених (стохастичних) економічних об’єктів і процесів, коли не повністю (до певної міри) відомими є внутрішні взаємодії в цих системах.

Цей метод полягає у модельному відтворенні процесу за допомогою стохастичної математичної моделі та обчисленні характеристик цього процесу. Одне таке відтворення можливого (випадкового) стану функціонування модельованої системи називають реалізацією (чи імітаційним прогоном; далі — прогоном).

Після кожного прогону реєструють сукупність параметрів, що характеризують випадкову подію (її реалізацію). Метод ґрунтується на багатократних прогонах (випадкових реалізаціях) на підставі побудованої моделі з подальшим статистичним опрацюванням отриманих даних з метою визначення числових характеристик досліджуваного об’єкта (процесу) у вигляді статистичних оцінок його параметрів. Процес моделювання економічної системи зводиться до машинної імітації досліджуваного процесу, котрий моделюється на ЕОМ з усіма суттєвими невизначеностями, випадковостями і породженим ними ризиком. Імітаційне моделювання нерідко має назву симулятивного моделювання. Перші відомості про метод Монте-Карло були опубліковані в кінці 40-х рр. ХХ століття. Авторами методу є американські математики — економісти Дж. Нейман і С. Улам.

Теоретичною основою методу статистичного моделювання є закон великих чисел. У теорії ймовірностей закон великих чисел ґрунтується на доведенні низки теорем для різних умов збіжності за ймовірністю середніх значень результатів (на підставі великої кількості спостережень) до деяких величин.

Під законом великих чисел розуміють кілька теорем. Наприклад, одна з теорем П. Л. Чебишева формулюється таким чином: «За необмеженого збільшення кількості незалежних випробувань (n) середнє арифметичне вільних від систематичних помилок і рівноточних результатів спостережень xi випадкової величини x, яка має скінченну дисперсію D(x), збігається за ймовірністю до математичного сподівання mx = M(x) цієї випадкової величини».

Це можна записати так:

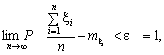 (5.1)

де e — як завгодно мале додатне число.

Теорема Бернуллі формулюється так: «За необмеженого збільшення числа незалежних спроб (п) за одних і тих самих умов відносна частота  настання випадкової події збігається за ймовірністю до р, тобто:

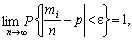 (5.2)

де e — як завгодно мале додатне число».

Згідно з цією теоремою для отримання ймовірності певної події, наприклад імовірності станів деякої системи 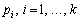, обчислюють відносні частоти  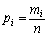для кількості реалізацій, що дорівнює n. Результати усереднюють і з деяким наближенням одержують шукані ймовірності станів системи. Чим більшим буде n, тим точнішим буде результат обчислення цих імовірностей. Це легко довести.

Припустимо, що треба відшукати значення математичного сподівання m для певної випадкової величини. Підберемо таку випадкову величину x, щоб

M(x) = m, а D(x) = b2 ,

де b2 — довільне значення дисперсії випадкової величини x.

Розгляньмо послідовність n незалежних випадкових величин 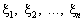 , розподіл імовірностей яких збігається з розподілом x. Якщо n є досить великим, то згідно з центральною граничною теоремою розподіл суми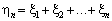 

буде приблизно нормальним розподілом з параметрами a = n • m; s2 = n • b2.

З правила «трьох сигм» 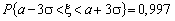 випливає, що

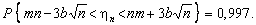 (5.3)

Розділивши нерівність, що розташована у фігурних дужках, на n, oтримаємо еквівалентну нерівність з тією самою ймовірністю:

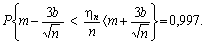
Це співвідношення можна записати у вигляді:

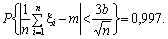(5.4)

Співвідношення (5.4) визначає метод обчислення середнього значення m і оцінку похибки. З (5.4) видно, що середнє арифметичне реалізацій випадкової величини x наближено дорівнюватиме числу m. З імовірністю р = 0,997 похибка такого наближення не перевищує 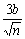. Очевидно, що ця похибка прямує до нуля зі зростанням n, що й потрібно було довести.

Розв’язування задач методом статистичного моделювання полягає в такому:

·                      опрацювання й побудова структурної схеми процесу, виявлення основних взаємозв’язків;

·                      формалізований опис процесу;

·                      моделювання випадкових явищ (випадкових подій, випадкових величин, випадкових функцій), що притаманні досліджуваній системі;

·                      моделювання процесу функціонування системи (на підставі використання даних, що отримані на попередньому етапі) — відтворення процесу відповідно до розробленої структурної схеми і формалізованого опису (імітаційні прогони);

·                      накопичення результатів моделювання (імітаційних прогонів), статистичне опрацювання, аналіз та інтерпретація їх.

Зазначимо, що будь-які твердження стосовно до характеристик модельованої системи повинні ґрунтуватися на результатах відповідних перевірок за допомогою методів математичної статистики.

Оскільки випадкові події й випадкові функції можуть подаватися з використанням випадкових величин, то й моделювання випадкових подій і випадкових функцій проводиться за допомогою випадкових величин.

 

Моделювання випадкових величин. Для моделювання випадкової величини потрібно знати закон її розподілу. Найзагальнішим способом отримання послідовності випадкових чисел, що є послідовністю реалізацій випадкової величини, котра розподілена за довільним законом, є спосіб, в основі якого — процес формування їх з вихідної послідовності випадкових чисел. Ця послідовність є послідовністю реалізацій випадкової величини, що розподілена в інтервалі (0; 1) згідно з рівномірним законом розподілу.

Згадану послідовність випадкових чисел з рівномірним законом розподілу можна отримати трьома способами:

·                      використанням таблиць випадкових чисел;

·                      застосуванням генераторів випадкових чисел;

·                      методом псевдовипадкових чисел.

Нині використовують псевдовипадкові числа, що відповідають рівномірному закону розподілу. Псевдовипадкові (випадкові) числа— це числа, отримані за деяким правилом (формулою), що імітує значення випадкової величини. Розроблено низку алгоритмів для отримання псевдовипадкових чисел. Датчики псевдовипадкових чисел є складовими більшості програмних комплексів.

Для перетворення послідовності випадкових чисел, що є реалізаціями випадкової величини з рівномірним законом розподілу в інтервалі (0; 1), у послідовність випадкових чисел, що є реалізаціями випадкової величини із заданою інтегральною функцією розподілу F(x), треба із сукупності випадкових чисел з рівномірним законом розподілу в інтервалі (0; 1) вибрати випадкове число ? і розв’язати рівняння:

F(x) = x відносно х. (5.5)

У випадку, коли задана функція щільності ймовірності f(x), співвідношення (3.5) набирає вигляду:

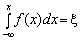 (5.6)

Для низки законів розподілу отримано аналітичний розв’язок рівняння (3.6), результат якого наведено в таблиці 5.1.

Таблиця 5.1

Формули для моделювання випадкових величин

Закони розподілу випадкової величини	Щільність розподілу	Формули для моделювання випадкових величин
Експоненційний
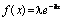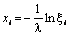Вейбула
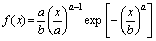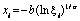Гама-розподіл (? — цілі числа)
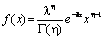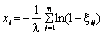Нормальний

 

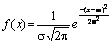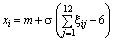Моделювання випадкових подій. Моделювання випадкових подій полягає у відтворенні факту появи чи непояви випадкової події відповідно до заданої ймовірності. Моделювання повної групи несумісних подій А1, А2, …, Аn, імовірності котрих P(Ai) = pi, i = 1, …, n відомі, можна привести до моделювання дискретної випадкової величини Y, яка має закон розподілу P(yi) = pi, де ймовірність її можливих значень

P(yi) = P(Ai) = pi.

Тобто прийняття дискретною випадковою величиною Y можливого значення yі еквівалентне появі події Аі. Для практичної реалізації даного способу спочатку на одиничному відрізку числової осі відкладають інтервали Di = pi.

Генерують рівномірно розподілену на інтервалі (0; 1) випадкову величину, реалізацією котрої є випадкове число xj, і перевіряють умову:

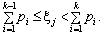  (5.7)

При виконанні умови (5.7) вважають, що за цього випробування відбулася подія Аk.

Приклад. Імовірність появи події А у кожному випробуванні дорівнює Р(А) = 0,75. Необхідно змоделювати три випробування і визначити послідовність реалізації події А.

Розв’язання. Відкладемо на одиничному відрізку числової осі точку Е = 0,75 і вважатимемо, що коли випадкове число xі < E, то у випробуванні настала подія А. У протилежному випадку (при 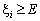) настала подія не А (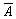), тобто подія А не мала місця.

Припустимо, наприклад, що з відповідної таблиці обрані випадкові числа x1 = 0,925, x2 = 0,135, x3 = 0,088. Тоді за трьох випробувань отримаємо таку послідовність реалізації подій: 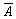А, А.

Моделювання сумісних (залежних і незалежних) подій можна виконати двома способами.

Перший спосіб. На першому етапі моделювання визначають усі можливі варіанти появи сумісних подій у випробуванні. Знаходять повну групу несумісних подій та обчислюють їх імовірності.

На другому етапі вчиняють так само, як і в моделюванні повної групи несумісних подій.

Приклад. Нехай при випробуванні мають місце залежні й сумісні події А та В, при цьому відомо, що Р(А) = 0,7; Р(В) = 0,5; Р(АВ) = 0,3.

Потрібно змоделювати появу подій А та В у двох випробуваннях.

Розв’язання. У кожному випробуванні можливі чотири несумісних результати, тобто настання чотирьох подій:

·                      С1 = АВ, Р(С1) = Р(АВ) = 0,3.

·                      С2 =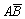, Р(С2) = Р() = Р(А) – Р(ВА) = 0,7 – 0,3 = 0,4.

·                      С3 =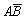, Р(С3) = Р(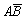) = Р(В) – Р(АВ) = 0,5 – 0,3 = 0,2.

·                      С4 =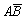,  Р(С4) = 1 – [Р(С1) + Р(С2) + Р(С3)] = 1 – (0,3 + 0,4 + + 0,2) = 0,1.

Змоделюймо повну групу подій С1, С2, С3, С4 у двох випробуваннях (прогонах). Попередньо на одиничному відрізку числової осі (рис. 5.1) послідовно відкладемо інтервали:

Dі = Р(Сі), і = 1,…, 4.

Рис. 5.1. Інтервали Dі = Р(Сі)

 

Нехай отримано (взято з відповідної таблиці) випадкові числа x1 = 0,68 і x2 = 0,95. Випадкове число x1 належить до інтервалу D2, тому при першому випробуванні мала місце подія А, а подія В не настала. За другого випробування випадкове число x2 належить до інтервалу D4. Обидві події А та В не мали місця.

Другий спосіб. Моделювання сумісних подій полягає у розігруванні факту появи кожної із сумісних подій окремо, при цьому, якщо події залежні, треба попередньо визначити умовні ймовірності.

Приклад. Використовуючи умови попереднього прикладу, потрібно змоделювати окрему появу подій А та В в одному випробуванні.

Розв’язання. Події А та В є залежними, тому попередньо знаходимо умовні ймовірності Р(В/А) та Р():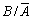

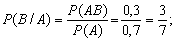
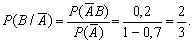
Для моделювання події А обрано випадкове число x1. Нехай x1 = 0,96. Оскільки x1>P(A), то подія А у випробуванні не настала.

Тепер розіграємо подію В за умови, що подія А у випробуванні не мала місця. Нехай випадкове число x2 = 0,22. Отже, 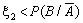 (0,22 < 2/3), тобто маємо, що подія В за випробування настала.