Тема 5. Алгоритмічні (імітаційні) і рейтингові моделі бізнес-проєктування
8. Моделі й методи процесу обчислення рейтингу економічної системи
Адекватною
математичною моделлю для аналізу набору показників є система S, що
визначається як n-арне відношення. Будь-яка методика обчислення рейтингу
зводиться до послідовної факторизації набору з n вихідних показників,
результатом якої є елемент лінійно впорядкованої (напівупорядкованої) множини.
Уніфікованим засобом опису процесу обчислення рейтингу на підставі аналізу
комплексних оцінок (незалежно від конкретної методики) може бути його подання у
вигляді дискретного перетворення М. Областю дії такого перетворення є п-мірний
масив А, де п — кількість використаних комплексних характеристик. Кожен індекс
масиву відповідає одній із комплексних характеристик, а значення цього індексу
— допустимі значення оцінок характеристики (обчислені за відповідною шкалою). Перетворювач М
функціонує таким чином. Якщо кількість вимірюваних характеристик дорівнює
розмірності масиву, то М просто здійснює вибір елемента масиву. Якщо ж
кількість обчислюваних характеристик менша, ніж розмірність масиву, то
перетворювач М функціонує таким чином. Нехай задано
набір значень Важливу роль у
переході від системи S до перетворювача М відіграють методи
прогнозування (як статистичні, так і експертні) та класифікація економічних
об’єктів (кластерний аналіз). Нехай U =
{u1, …, un} — універсальна множина вихідних показників. Область
значень показника ui(i = 1, …, n) позначимо через na1i
і припустимо, що Нехай Використаймо таку
форму запису: Позначимо через тоді і лише тоді,
коли для будь-яких наборів Вважатимемо, що
методики А та В 1. 2. Фактор-множина Тому доводиться
теорема 1. Якщо D —
замкнена множина і Значення теореми
1 полягає в такому. Якщо множина типових (в умовах, що розглядаються) наборів
показників належить множині У решті випадків
виникає проблема щодо обрання допустимої методики, розв’язання якої можна
отримати лише в разі використання експертних методів. Доводяться й інші важливі
теореми. Зведення проблеми
обчислення рейтингу до проблеми класифікації економічних об’єктів дає
можливість застосовувати стандартну техніку декомпозиції кваліметричних моделей
для підвищення ефективності обчислень. 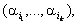
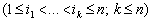 , характеристик, що
визначаються індексами
, характеристик, що
визначаються індексами 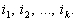 Реакцією перетворювача
М за вхідних даних
Реакцією перетворювача
М за вхідних даних 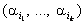 є такі три числа
є такі три числа 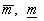 та
та 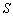 , що
, що 
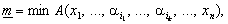 де максимум і мінімум
беруться за всіма допустимими значеннями
де максимум і мінімум
беруться за всіма допустимими значеннями 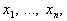 а S — середнє
значення (тобто математичне сподівання) по всіх допустимих значеннях. Числа
а S — середнє
значення (тобто математичне сподівання) по всіх допустимих значеннях. Числа  та
та 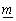 називають відповідно
оптимістичним і песимістичним рейтингами. У подальшому трійка (
називають відповідно
оптимістичним і песимістичним рейтингами. У подальшому трійка (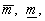 S) може бути перетворена в те чи інше число
відповідно до обраної методики.
S) може бути перетворена в те чи інше число
відповідно до обраної методики.Рейтинг як засіб класифікації економічних об’єктів. Сутність рейтингу полягає в оцінюванні позиції
аналізованого об’єкта на обраній шкалі. Ця обставина однозначно визначає
обчислення рейтингу як спеціальним чином деталізованого варіанта загальної
проблеми класифікації економічних (соціально-економічних) об’єктів. Розгляньмо
особливості цієї деталізації.
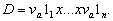
![]() — фіксована скінченна
множина методик обчислення рейтингу. Шкалу, обрану для методики
— фіксована скінченна
множина методик обчислення рейтингу. Шкалу, обрану для методики 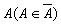 , позначимо через Шa. Таким чином, методика
, позначимо через Шa. Таким чином, методика 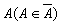 реалізує відображення
реалізує відображення 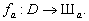
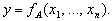
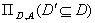 розбиття множини А,
що визначається таким чином:
розбиття множини А,
що визначається таким чином: 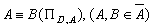
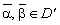 справедливим є
співвідношення
справедливим є
співвідношення 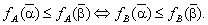
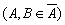 :
: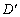 — узгоджені, якщо
— узгоджені, якщо 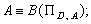
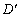 — суперечливі, якщо
— суперечливі, якщо 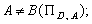
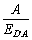 (де
(де 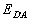 — еквівалентність, що
відповідає розбиттю
— еквівалентність, що
відповідає розбиттю 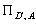 ) визначає усі типи суперечностей між методиками, які
належать до множини А та які виникають за обчислення рейтингу на множині
) визначає усі типи суперечностей між методиками, які
належать до множини А та які виникають за обчислення рейтингу на множині
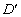 . Верхній та нижній конуси підмножини позначимо, відповідно,
через ВК(Х) та НК(Х).
. Верхній та нижній конуси підмножини позначимо, відповідно,
через ВК(Х) та НК(Х).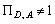 (?
(?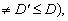 то існує такий перетин
то існує такий перетин 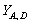 множини
множини 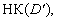 що складається з
попарно непорівнянних за включенням елементів, для котрих
що складається з
попарно непорівнянних за включенням елементів, для котрих 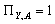 для будь-якого
для будь-якого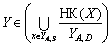 і
і 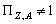 для будь-якого
для будь-якого 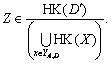
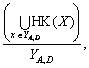 то в обчисленні
рейтингу може використовуватися будь-яка методика
то в обчисленні
рейтингу може використовуватися будь-яка методика 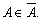
Шрифти
Розмір шрифта
Колір тексту
Колір тла
Кернінг шрифтів
Видимість картинок
Інтервал між літерами
Висота рядка
Виділити посилання
Вирівнювання тексту
Ширина абзацу
