Лекція 6. Синхронні і асинхронні електричні машини

В режимі двигуна частота (^п) обертання ротора асинхронної машини завжди менша за частоту обертання (^п₁) магнітного поля статора. Саме ця особливість і визначає назву двигуна такого типу – асинхронний.

Величина, що характеризує різницю частот обертання ротора і магнітного поля статора, виражена у відносних одиницях або процентах, зветься ковзанням. Математично ковзання подається як:

.

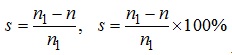З наведеної формули випливає, що ковзання асинхронного двигуна змінюється в діапазоні 0<s≤1.

В режимі роботи двигуна без навантаження на валу (режим холостого ходу машини) ротор обертається з частотою лише трошки меншою за частоту обертання магнітного поля, яку в подальшому називатимемо синхронною частотою. В цьому випадку ковзання мало відрізняється від нуля. Однак, струм холостого ходу двигуна складає (20 … 40 %) від номінального струму статора. Це пояснюється тим, що обов’язково присутній повітряний зазор між статором і ротором підвищує магнітний опір магнітного кола двигуна для магнітного потоку.

Ковзання, яке відповідає номінальному навантаженню двигуна зветься номінальним ковзанням.

Для асинхронних двигунів номінальне ковзання складає (1 … 8 %). Менші значення ковзання відповідають двигунам більшої потужності, великі значення ковзання притаманні двигунам малої потужності.

Частота обертання ротора (в об/хв.) може бути визначена, якщо відомі синхронна частота магнітного поля статора п₁ і ковзання, а саме:

.

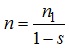Наприклад, для двигуна загальнопромислового призначення (f = 50 Гц), який має чотири полюси (тобто дві пари полюсів – р=2) і номінальне ковзання 4%, частота обертання ротора становитиме:

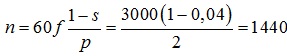, об/хв.

Частота струму в обмотці ротора, пропорційна абсолютній різниці синхронної частоти і частоти обертання ротора, зветься частотою ковзання. Частота ковзання розраховується як:

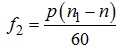, Гц.

Помноживши чисельник і знаменник співвідношення для частоти ковзання на значення синхронної частоти, отримуємо можливість розраховувати частоту ковзання через відомі значення частоти напруги живлення і величини ковзання, а саме:

,

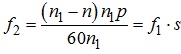де f1 = f - частота струму в статорі, яка співпадає з частотою мережі живлення.

Наприклад, для частоти мережі живлення f = 50 Гц при ковзанні s = (2 … 8 %) частота ковзання становитиме f₂ = (1 … 4 ) Гц.

Звичайно, величина частоти ковзання відбиватиметься на електричних параметрах кола ротора, а саме на ЕРС і реактивному опорі. ЕРС обмотки ротора Е_2s можна розрахувати як:

,

де к_об - коефіцієнт, який враховує специфіку виконання обмотки ротора (обмотковий коефіцієнт);

w₂ - кількість витків обмотки ротора;

Ф_т - амплітуда магнітного потоку.

У випадку нерухомого ротора, тобто за умови s=1, частота ковзання f2 дорівнюватиме частоті f₁=f напруги живлення двигуна, а отже E_2s=E₂.

За умови обертання ротора, коли f₂=f_1s, формула для розрахунку ЕРС приймає вигляд:

.

Аналогічний зв'язок можна встановити і між індуктивними опорами нерухомого x_2s ротора й ротора, що обертається, x₂, а саме:

.

Приклад. Для трифазного асинхронного двигуна відомо, що при частоті мережі електроживлення f=50 Гц, ЕРС і індуктивний опір нерухомого ротора дорівнюють відповідно E₂=120 В, X₂=130 Ом.

Визначити частоту струму в якорі, ЕРС на його затискачах, та індуктивний опір обмотки якоря під час обертання з ковзанням s=4 %. Користуючись наведеними формулами неважко отримати:

.

Механічна потужність асинхронного двигуна

Трифазний асинхронний двигун навантажує мережу живлення активною потужністю:

,

де:

- індекс «^Ф» позначає фазні значення напруги і струму обмотки статора,

- індекс «_л» позначає лінійні значення напруги мережі живлення і струму, що споживається двигуном.

В подальшому, як і раніше, індексом «₁» будемо позначати параметри обмотки статора, а індексом «₂» параметри обмотки ротора.

Процес перетворення електричної енергії в механічну найпростіше показати у вигляді енергетичної діаграми, наведеної на рис. 6.28.

З наведеної діаграми видно, що перетворення електричної енергії мережі живлення у механічну енергію на валу двигуна відбувається поетапно і супроводжується відповідними втратами енергії на кожному етапі. Ці втрати енергії зазвичай називають втратами потужності.

На підставі енергетичної діаграми двигуна можна визначити механічну потужність Р_мех, яка розвивається (віддається) двигуном (на валу), шляхом відрахування з потужності, що споживається з електричної мережі втрат на кожному етапі перетворення (передачі) енергії. До таких втрат відносяться втрати в обмотці статора, в сталі осердя і в обмотці ротора (механічними втратами в елементах кріплення валу й т.п. зазвичай нехтують).

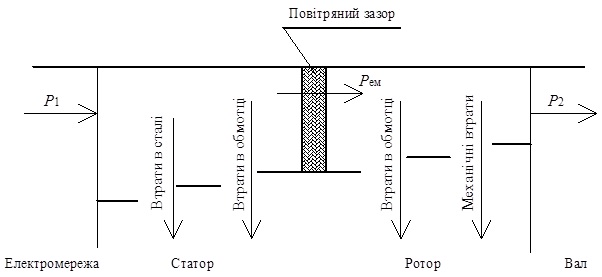
Рис. 6.7. Енергетична діаграма процесу перетворення електричної енергії в механічну

Рівняння енергетичного балансу двигуна можна записати як:

де т₂ - число фаз обмотки ротора за умови фазного способу його виконання або кількість стержнів ротора, поділене на два, якщо обмотка ротора виконана короткозамкненою;

Р_ст - втрати в сталі осердя ротора.

Втратами в сталі ротора зазвичай можна нехтувати, адже частота струму ротора надто мала. Електромагнітна потужність Р_ем, що передається ротору, визначається як добуток числа фаз, ЕРС, струму і коефіцієнта потужності ротора. Частина цієї потужності розсіюється в роторі у вигляді тепла.

Таким чином, механічну потужність асинхронного двигуна можна визначити як різницю між електромагнітною потужністю і втратами в обмотці ротора, а саме:

.

Це співвідношення можна подати в дещо іншому вигляді, якщо врахувати, що:

,

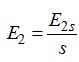а добуток

визначає активну складову ЕРС ротора.

З урахуванням наведеного, співвідношення для механічної потужності прийме вигляд:

.

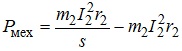Після деяких очевидних перетворень останнього співвідношення, отримуємо:

.

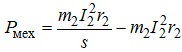Якщо це співвідношення подати у вигляді:

,

то стає зрозумілим, що зі збільшенням ковзання збільшуватиметься і нагрівання ротора. Саме тому сучасні асинхронні двигуни розраховують так, щоб в робочому режимі ковзання було мінімальним.

Корисна механічна потужність Р₂ на валу двигуна звичайно буде менша механічної потужності Р_мех, яку розвиває двигун, на величину механічних втрат, обумовлених тертям у підшипниках, а також тертям ротора о повітря.

Обертовий момент і його залежність від величини ковзання

Обертовий момент М двигуна пов'язаний з механічною потужністю Р_мех і кутовою частотою Ω₂ обертання ротора відомою з механіки формулою:

.

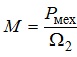Механічна потужність і її залежність від параметрів ротора з урахуванням отриманих вище співвідношень може бути подана як:

.

Зв'язок між кутовою частотою обертання ротора і магнітним полем статора можна подати через ковзання як:

.

Якщо обмотка статора має одну пару полюсів, то:

,

тобто кутова частота обертання магнітного поля статора дорівнюватиме круговій частоті струму в мережі живлення.

Однак в загальному випадку двигун має декілька пар полюсів. А тому:

.

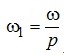при цьому співвідношення для кутової частоти ротора набуває вигляду:

.

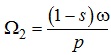Враховуючи наведене, співвідношення для обертового моменту можна записати як:

.

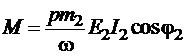Введемо позначення:

.

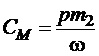Величина C_M, як видно з наведеного виразу, є постійною, яка визначається параметрами двигуна і мережі живлення. З урахуванням введеного позначення обертовий момент двигуна запишеться як

.

Аналіз останнього співвідношення показує, що обертовий момент двигуна пропорційний добутку струму і ЕРС ротора. а також залежить від кута зсуву фаз між ними.

Зупинимось на впливі ковзання на окремі множники наведеного співвідношення, якими, власне і визначається обертовий момент двигуна.

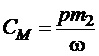 - постійна для даного типу двигуна величина, яка залежить лише від його конструктивних особливостей;

  - ЕРС, яка наводиться в обмотці нерухомого ротора;

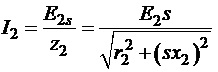 - струм у фазі обмотки ротора, який обертається; цей струм при збільшенні ковзання зростає, а при зменшенні ковзання – зменшується;

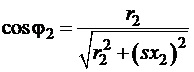 - фазовий кут між ЕРС та струмом в обмотці ротора; цей кут зменшується при збільшенні ковзання і збільшується при зменшенні ковзання.

Таким чином, з трьох основних параметрів ротора лише два залежать від ковзання, причому один з цих параметрів змінюється прямо пропорційно, а другий зворотно пропорційно ковзанню.

Наведене призводить до характерної нелінійності залежності обертового моменту асинхронного двигуна від ковзання (рис. 6.8).

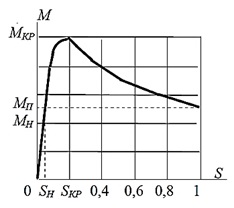
Рис. 6.8. Залежність обертового моменту асинхронного двигуна від ковзання

Характерними точками наведеної на рис. 6.8 залежності є:

М_П - пусковий момент, який відповідає ковзанню s=1, тобто нерухомому ротору;

M_Н - номінальний момент, який відповідає номінальному значенню ковзання s=s_H, тобто робочому режиму двигуна;

М_КР - критичний момент, тобто найбільше значення обертового моменту, який відповідає критичному значенню ковзання s=s_KP.

Значення критичного моменту визначає границю між областями стабільної і нестабільної роботи двигуна.

Двигун працюватиме в стабільній зоні, якщо при збільшенні моменту опору на валу обертовий момент зростає. Ковзання в цій області змінюється від нуля до критичного значення.

Якщо при збільшенні моменту опору ковзання збільшується, а обертовий момент зменшується, то двигун працюватиме у нестабільній області, що врешті-решт приводить до його зупинки. Ковзання в цій області більше критичного, але менше або дорівнює одиниці. З фізичної точки зору зменшення величини обертового моменту в цій зоні пояснюється зменшенням активної складової струму ротора, що приводить до зменшення величини cosφ.

Залежність обертового моменту від частоти обертання ротора називається механічною характеристикою.

Узагальнений вид механічної характеристики показаний на рис. 6.9.

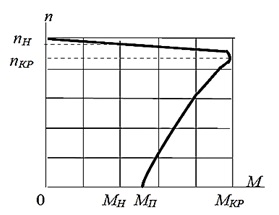
Рис. 6.9. Залежність обертового моменту асинхронного двигуна від частоти обертання ротора (механічна характеристика)

На механічній характеристиці асинхронного двигуна можна виділити ті самі характерні точки, і області, що і на розглянутій вище залежності обертового моменту асинхронного двигуна від ковзання. Аналогічні, звичайно, і явища, що супроводжують функціонування двигуна в кожній з цих зон.