Лекція 7. Трансформатори

Електрична схема однофазного трансформатора з двома обмотками  наведена на рис. 7.6.

Для визначеності припустимо, що до виводів другої обмотки наведеного на рис. 7.6 трансформатора підключене навантаження:

.

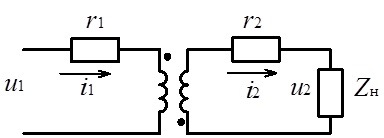
Рис. 7.6. Електрична схема однофазного трансформатора з двома обмотками

 

Для наведеної схеми на підставі другого закону Кірхгофа маємо:

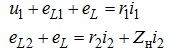                           (7.8)

Розкриваючи у співвідношенні (7.8) зміст електрорушійних сил самоіндукції та взаємної індукції, а також враховуючи, що:

,

отримуємо:

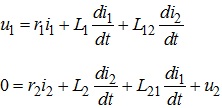                                      (7.9)

За умови, що напруга u₁ змінюється за гармонічним законом, та врахувавши співвідношення:

,

рівняння (7.9) можна записати в комплексній формі, а саме:

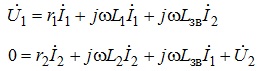                                           (7.10)

Введемо позначення:

                                       (7.11)

З урахуванням (7.11) співвідношення (7.10) можна подати як:

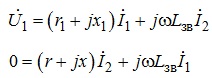                                           (7.12)

 

Розв’язавши систему рівнянь (7.12), наприклад, методом підстановки, отримуємо:

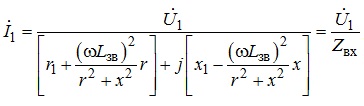                                         (7.13)

де  - комплексний вхідний (еквівалентний) опір всього електричного кола, утвореного трансформатором та опором навантаження.

Зі співвідношення (7.13) видно, що еквівалентний активний опір більше за опір r₁ первинної обмотки трансформатора.

Збільшення еквівалентного активного опору пов’язане з тим, що незворотне перетворення енергії в контурі вторинної обмотки відбувається за рахунок енергії, яка передається до контуру вторинної обмотки від контуру первинної обмотки, де саме й підключене джерело електричної енергії. Оскільки для заданого струму активна потужність, що визначає незворотні перетворення енергії, прямо пропорційна активному опору, то поглинання енергії у вторинному контурі приводить до збільшення опору всього кола.

Еквівалентний активний опір може бути:

- більше x₁, за умови (x<0),

- менше x₁, за умови (x>0).

 

Фізичну картину процесів, що відбуваються в електричному колі з трансформатором при вказаних варіантах, можна проілюструвати за допомогою векторних діаграм.

На рис. 7.7 представлені граничні випадки, коли контур вторинної обмотки має чисто реактивний (індуктивний – рис. 7.7(а) або ємнісний – рис. 7.7(б)) характер.

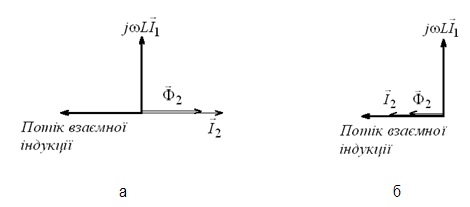
Рис. 7.7. Векторні діаграми за умови індуктивного (а) та ємнісного (б) характеру опору контуру вторинної обмотки

 

При індуктивному характері опору контуру вторинної обмотки (рис. 7.7, а) магнітний потік, який утворюється струмом цього контуру, буде зменшувати потік взаємної індукції, що веде до зменшення реактивного опору контуру первинної обмотки.

При ємнісному характері опору контуру вторинної обмотки (рис. 7.7,б) навпаки, магнітний потік, який утворюється струмом цього контуру, сприятиме збільшенню потоку взаємної індукції, а отже приводить до збільшення реактивного опору контуру вторинної обмотки трансформатора.

Повертаючись до умов електричної рівноваги в контурах первинної та вторинної обмоток, які відображаються співвідношеннями (7.8), неважко помітити, що вони рівносильні наступним рівнянням

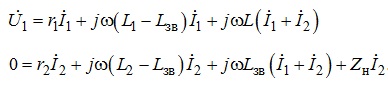                                   (7.14)

Схема електричного кола, яке описуватиметься системою рівнянь (7.14), має вигляд як на рис. 7.8.

В наведеній на рис. 7.8 схемі струми I₁, I₂ та напруги U₁, U₂ дорівнюють відповідним струмам та напругам притаманним реальному трансформатору, а отже наведена схема є еквівалентною електричною схемою трансформатора (або еквівалентною схемою заміщення трансформатора).

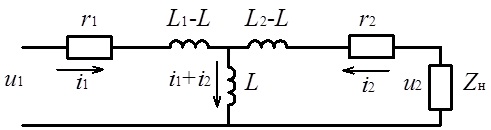
Рис. 7.8. Еквівалентна електрична схема трансформатора

 

Як відомо, ступінь магнітного зв’язку контурів прийнято характеризувати величиною:

.

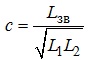Величина c зазвичай зветься коефіцієнтом зв’язку котушок, індуктивності яких становлять L₁, L₂ при величині їх взаємної індуктивності L_зв.

Оскільки у природі не існує магнітних ізоляторів, то завжди має місце розсіювання магнітного потоку. Тобто в реальних випадках завжди:

.

Таким чином, за умови, що:

,

мають виконуватися співвідношення:

.

Видно, що за умови неоднакових значень L₁, L₂ одна з наведених різностей може виявитися від’ємною. Отже, різності:

у співвідношенні (7.14) матимуть фізичний зміст лише за умови однакової кількості витків первинної та вторинної обмоток трансформатора, представляючи індуктивності розсіювання L_1s, L_2s відповідних обмоток трансформатора.

При неоднаковій кількості витків обмоток на практиці зазвичай використовують так звану приведену схему заміщення трансформатора (рис. 7.9).

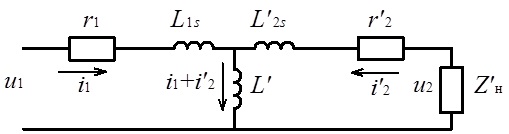
Рис. 7.9. Приведена схема заміщення трансформатора

 

Процедура переходу до приведеної схеми заміщення трансформатора полягає в тому, що напруга U₂ та струм I₂ у контурі вторинної обмотки трансформатора замінюються фіктивними їх значеннями, які визначаються так щоб збереглися енергетичні співвідношення в еквівалентній схемі заміщення та в реальному трансформаторі.

 

Дотримуючись вказаного правила, матимемо:

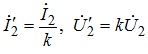                                              (7.15)

де 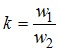 - визначена вище константа, яка зветься коефіцієнтом трансформації трансформатора.

 

Таким чином, співвідношення (7.14) для приведеної ЕСЗ матимуть вигляд:

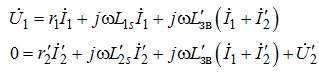                                       (7.16)

де

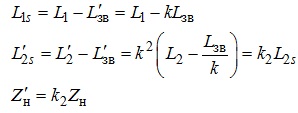                                  (7.17)

Індуктивні опори  являють собою опори розсіювання відповідних обмоток, а індуктивний опір  - опір вітки намагнічування. Відповідно струм, що тече в цій вітці і дорівнює 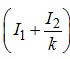, зветься струмом намагнічування (намагнічуючим струмом) трансформатора.