Тема 6. Теорія фірми: мікроекономічна модель підприємства (2 години)

Отже, фірма поток ресурсів перетворює в поток грошової продукції. Розглянемо цей процес. Власне, це і є виробництво.

Виробнича функція – це залежність між структурою затрат ресурсів і максимально можливим випуском продукції.

Виробнича функція показує, який максимальний обсяг випуску Q, може бути одержаний при кожному конкретному наборі (L,K) витрачених ресурсів і незмінній технології.

Зміна технології веде до зміни самої функціональної залежності.

В залежності від кількості факторів, виробнича функція буває однофакторна, двофакторна, багатофакторна.

Класичний приклад виробничої функції – це двофакторна виробнича функція, яка встановлює зв’язок між виробництвом продукції та витратами двох основних факторів виробництва – капіталу (K) і праці (L) : Q = F (K, L)

Приклад однофакторної функції: Q = F (L)

графік

Збільшення кількість праці від L₁ до L₃ спочатку веде до росту ви пуску, по ходу це зростання уповільнюється, а після точки А – падіння обсягу випуску.

Виробнича функція відповідає закону спадної віддачі фактичного виробництва.

Тепер розглянемо 2-х факторну функцію.

Взагалі функціональна залежність може бути задана аналітично, табличній та графічно.

Ця таблиця має назву виробничої сітки.

В кожній клітинці – максимальний випуск, що забезпечується відповідними обсягами ресурсів.

Яке графічне зображення має двофакторна функція?

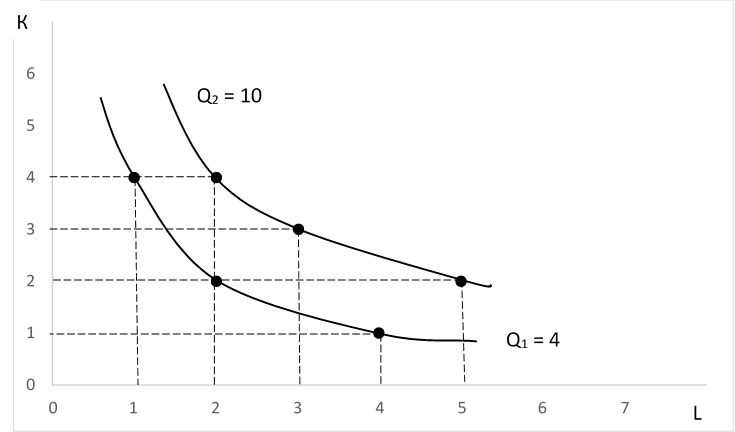
Із таблички вибираємо різні комбінації ресурсів, які забезпечують однаковий випуск. Наприклад Q₁ = 4,

К₁ = 4, L₁ = 1

К₂ = 2, L₂ = 2

К₃ = 1, L₃ = 4

Q₂ = 10:

К₁ = 4, L₁ = 2

К₂ = 3, L₂ = 3

К₃ = 2, L₃ = 5

З’єднавши ці точки плавною кривою, отримаємо ізокванту.

Ізокванта – лінія незмінного випуску. Показує всі можливі комбінації ресурсів (L, K), які дозволяють отримати певний фіксований обсяг виробництва (Q₁).

Сукупність ізоквант однієї виробничої функції, кожна з яких відповідає певному обсягу випуску продукції, називається картою ізоквант.

Властивості ізоквант:

1) дві ізокванти, що відповідають різним обсягам випуску, не можуть перетинатись;

2) чим далі розташована ізокванта від початку координат, тим більший випуск Q відповідає цій лінії;

3) ізокванти опуклі в бік початку координат.

Як задається аналітично виробнича функція?

Типовим прикладом ВФ в аналітичній формі запису може бути виробнича функція Коба-Дугласа:

Q = а×L^b×K^c

а, b, с > 0

b, с < 1

Ізокванти функціЇ Коба-Дугласа мають вигляд як на рисунку вище. Криві не перетинають координатних осей, а лише необмежено наближаються до них. Це означає, що фактори виробництва можуть лише частково замінювати один одного, але повна заміна неможлива, тобто

F(O,K)=F(L,O)=0

Далі розглянемо крайні випадки виробничої функції:

1) виробнича функція Леонт’єва:

Q = min(a×L, b×K)

a, b > 0

причому пропорції використання факторів виробництва є фіксованими. Неможливо виконати будь-яку заміну серед вхідних ресурсів. Кожен рівень виробництва вимагає певної комбінації праці і капіталу. Додатковий обсяг випуску можна отримати, коли праця і капітал додаються в певних пропорціях. Додаткова одиниця праці не збільшує виробництво так само, як і додаткова одиниця окремо взятого капіталу.

графік

2) Лінійна ВФ з повним заміщенням факторів виробництва:

Q = a×L + b×K

a, b > 0

Ресурси є абсолютними замінниками.

Нехай а=1, b=2 Q = L + 2×K

$K=\frac{Q- L }{2}$

Візьмемо Q = 2 і накреслимо графік:

$К=1 - \frac{L}{2}$

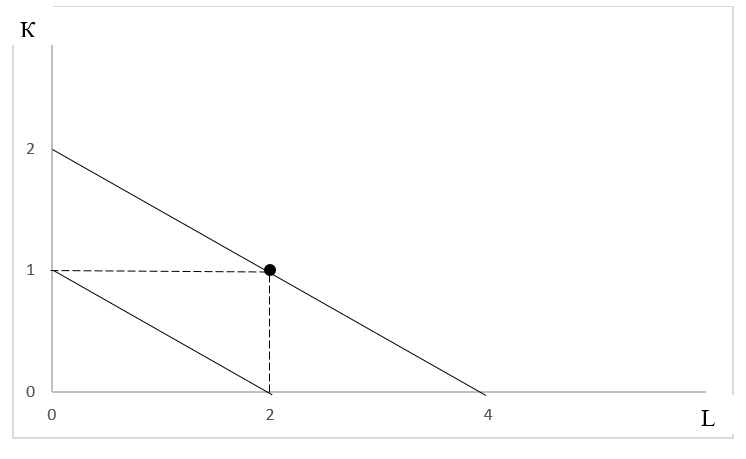
К₁ = 1, L₁ = 0

К₂ = 0, L₂ = 2

Нехай Q = 4: L₁ = 0, К₁ = 2, L₂ = 4, К₂ = 0.

$\frac{∆К}{∆L}=\frac{1}{2}=const$