Тема 8. Нелінійні розрахунки будівельних конструкцій
2. Розв’язування систем нелінійних рівнянь.
Розрахунок нелінійних систем є більш складним завданням в порівнянні з рішенням лінійних задач, оскільки тут доводиться враховувати деформований стан розглянутої області, відмовитися від принципу незалежності дії сил, застосовувати спеціальні методи пошуку і аналізу рішення. При цих умовах отримати аналітичний розв’язок задачі, як правило, не вдається, тому розрахунок виконується за допомогою чисельних методів, найчастіше МСЕ, використовуючи при цьому процедури послідовних наближень.
Методи, що розглядаються нижче, часто застосовуються для вирішення нелінійних задач. Усі вони засновані на лінеаризації нелінійних рівнянь, тобто пошук розв’язку нелінійних рівнянь здійснюється розв’язуванням рекурентної послідовності лінійних. Деякі з них порівняно мало відомі (метод послідовних жорсткостей), хоча у ряді випадків досить ефективні.
Розглянуті методи можна розділити на два класи:
1) ітераційні, для яких відома точність рішення, але невідома кількість обчислень (ітерацій), які знадобляться, щоб досягти задану точність:
- метод пружних розв’язків (рис. 8.2, а) – загальна матриця жорсткості представляється як сума лінійної та нелінійної складових;
- метод змінних жорсткостей (у математиці він відомий як метод січних, рис. 8.2, б) – загальна матриця жорсткості і-ї ітерації визначається на основі переміщень (і-1) ітерації;
- метод Ньютона-Рафсона (рис. 8.2, в) – на кожній ітерації визначається поправка на основі відхилення вузлових сил;
- метод Ньютона-Канторовича (рис. 8.2, г) – модифікований м-д Ньютона-Рафсона без перерахунку матриці жорсткості на кожній ітерації.
2) прямі, для яких заздалегідь відома кількість обчислень, але невідомо, яка буде досягнута точність. Сюди відносяться крокові методи:
- метод послідовних жорсткостей;
- метод послідовних навантажень з урахуванням нев’язок.
Відомі також і інші модифікації крокових методів. Більшість модифікацій крокових методів пов’язана з уточненням рішення на кожному або на наступних кроках.
Крокові методи знайшли дуже широке застосування, і це, разом з достатньо легкою реалізацією, пояснюється також можливістю організації комп’ютерного моделювання процесу навантаження або процесу зміни напружено-деформованого стану конструкції в часі, викликаного таким чинником, як повзучість.
При необхідності вирішення тільки нелінійної задачі, тобто визначення напружено-деформованого стану, відповідного заданому навантаженню, перевагу слід віддавати ітераційним методам. При необхідності проведення математичного моделювання процесу навантаження використовуються крокові методи.
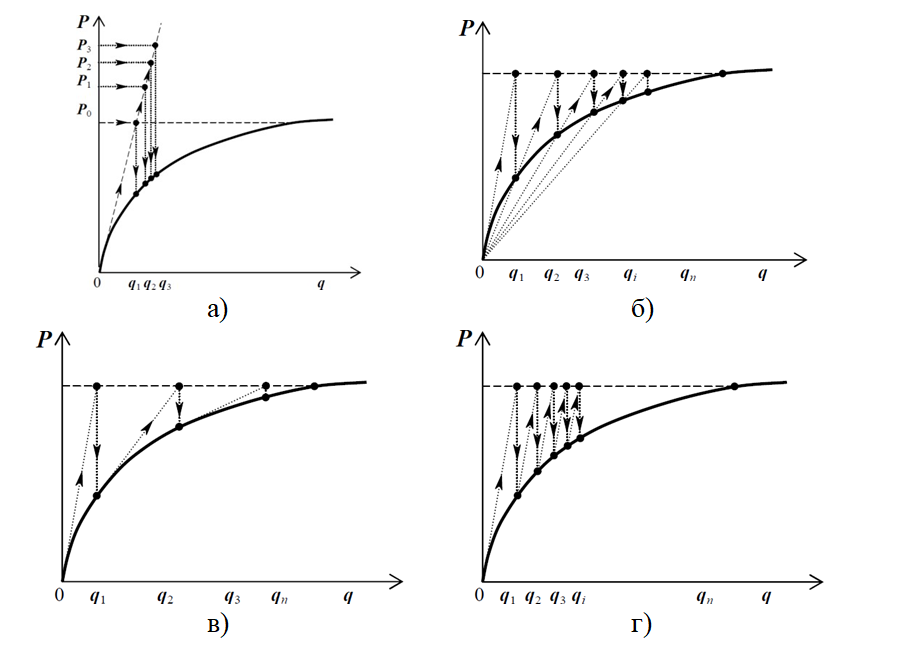
Рисунок 8.2 – Графічна інтерпретація ітераційних методів розрахунку
Шрифти
Розмір шрифта
Колір тексту
Колір тла
Кернінг шрифтів
Видимість картинок
Інтервал між літерами
Висота рядка
Виділити посилання
Вирівнювання тексту
Ширина абзацу
