Тема 8. Нелінійні розрахунки будівельних конструкцій

Відомі декілька варіантів крокової процедури, які відрізняються лише використовуваними методами чисельного рішення задачі Коші. Усі вони випробувані на практиці і мають свою сферу застосування. Так, в ПК ЛІРА є можливість використовувати наступні модифікації крокового методу:

• простий кроковий метод;
• кроковий метод з уточненнями;
• кроково-ітераційний.

У першому випадку на кожному кроці вирішується лінеаризована задача, і в припущенні, що це рішення є досить точним, реалізується перехід до наступного кроку навантаження (рис. 8.3, а). Погрішність розв’язку нелінійної задачі не контролюється – передбачається, що погрішність мала за рахунок вибору малого кроку чисельного інтегрування.

Другий варіант передбачає контроль нев’язок на кожному кроці та ітераційне уточнення навантаження чергового кроку за рахунок врахування нев’язки в рівняннях рівноваги (рис. 8.3, б).

Нарешті, в третьому випадку виробляється ітераційне уточнення рішення на кожному кроці з коригуванням лінеаризованої матриці жорсткості на кожній ітерації (рис. 8.3, в).

Важливою особливістю крокової процедури і її привабливою відмінністю від інших методів рішення нелінійних рівнянь є те, що лінеаризована в околі деякого навантаження система може аналізуватися звичайними методами лінійної будівельної механіки. Мають сенс оцінки коефіцієнта запасу стійкості або частоти і форми власних коливань такої лінеаризованої системи.

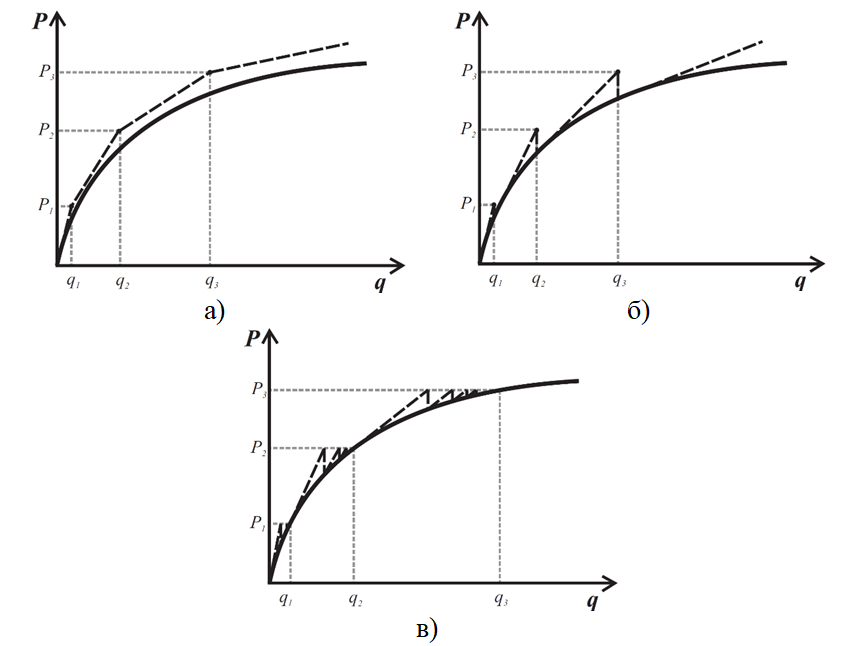
Рисунок 8.3 – Графічна інтерпретація крокових методів розрахунку

Необхідно відмітити, що дослідження поведінки нелінійної системи може вимагати перегляду прийнятої раніше розрахункової схеми, зокрема, збільшення деталізації скінченно-елементної сітки.

Для вирішення фізично і геометрично нелінійних завдань будівельної механіки кроковим методом в ПК ЛІРА призначений кроковий процесор ЛІР- СТЕП. Він організовує кроковий процес і забезпечує рішення лінеаризованої системи дозволяючих рівнянь на кроці для поточного приросту вектора вузлових навантажень, сформованого для конкретного навантаження.

Кроковий процесор дозволяє отримати напружено-деформований стан з урахуванням нелінійних ефектів як для мономатеріальних, так і для біматеріальних (залізобетон) систем. Для біматеріальних систем пропонується певний набір типів армуючих включень.

Матриця жорсткості лінеаризованої фізично нелінійної системи формується на основі змінних інтегральних жорсткостей, що отримуються в точках інтегрування скінченного елементу при вирішенні пружної задачі на конкретному кроці. Схема чисельного інтегрування по області скінченного елементу і набір використовуваних жорсткостей визначаються типом скінченного елементу. Для отримання відповідного набору інтегральних жорсткостей переріз скінченного елементу в точках інтегрування дробиться на ряд елементарних підобластей, в центрах яких визначаються нові значення фізико-механічних характеристик матеріалу, відповідно до заданої користувачем діаграми деформування матеріалу. На кожному кроці вирішується лінеаризоване завдання з формуванням векторів переміщень, зусиль і нових інтегральних жорсткостей із дотичного модуля для наступного кроку. Кількість кроків і коефіцієнти до навантаження задаються користувачем. В цьому випадку основне рівняння МСЕ має вигляд

[K (u)]{u} = {P}                                                                            (8.1)

де   [K (u)]    – матриця жорсткості, яка перераховується на кожному кроці з врахуванням поточного значення модуля пружності матеріалу.

ЛІР-СТЕП дозволяє комбінувати лінійні і нелінійні скінченні елементи, а також реалізовувати розрахунок за суперелементною схемою, якщо нелінійні елементи присутні тільки в основній схемі.

Для задання параметрів нелінійності у всіх діалогових вікнах задання характеристик жорсткості для стандартних перерізів додається група кнопок

«Врахування нелінійності», які стають активними після задання відповідного типу скінченних елементів.