Тема 10.1 Розрахунки з врахуванням геометричної та конструктивної нелінійності

Даний клас задач враховує зміну розрахункової схеми в процесі навантаження – виникнення нових в’язей чи усунення існуючих.

Діапазон можливих переміщень в цьому випадку задається односторонніми в’язями – елементами, які працюють тільки на розтяг або тільки на стиск. Математично описуються умовами-нерівностями для переміщень.

Системи, де обмеження на переміщення визначені умовами-нерівностями (односторонні в’язі) зустрічаються частіше, ніж про це звично думають. Конструкція, вільно оперта на деяку поверхню, котра забороняє переміщення у бік цієї поверхні і не перешкоджає переміщенню в протилежному напрямі, гнучкі нитки, які дозволяють зближуватися своїм кінцевим точкам і не дозволяють їм віддалятися більш ніж на довжину нитки є простими прикладами (рис 10.1). Типовими прикладами можуть також служити: кам’яна кладка, виконана насухо, зв’язок між фундаментом споруди і ґрунтом, що його підстилає. Сипучі ґрунти або абсолютно гнучкі мембрани можуть служити прикладами складніших систем з односторонніми в’язями.

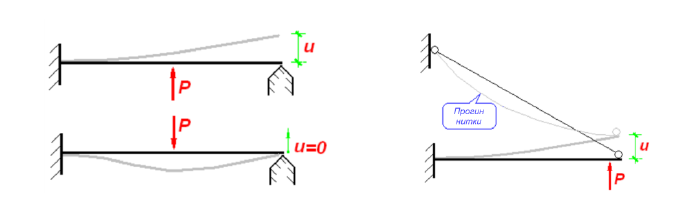
Рисунок 10.1 – Приклади конструктивної нелінійності

За традицією, такого роду в’язі розглядають як ідеальні двосторонні, перевіряючи апостеріорно чи не порушує отримане рішення характер роботи в’язей. Ця традиція склалася давно, коли вручну отримати рішення для правильно сформульованого завдання було досить складно, зараз же практично будь-який сучасний програмний комплекс такі завдання вирішує в правильній постановці.

Моделювання конструктивної нелінійності проводиться з допомогою одно- та двохвузлових СЕ односторонньої в’язі (СЕ №251, 252, 255, 256), які можуть знаходитися в одному з двох станів – робочому (в’язь включено) чи неробочому (в’язь виключено). Дані СЕ дозволяють врахувати нелінійність в’язей між вузлами розрахункової схеми або нерівність границь податливості в’язі в прямому і протилежному напрямах, коли граничне зусилля розтягу не рівне граничному зусиллю стиску.