Тема 5. Раціональне розбиття на скінченні елементи

Зрозуміло, всі ці переваги суперелементної моделі повною мірою проявляються лише у тому випадку, коли в системі є багато однакових суперелементів, що повторюються, в яких кількість внутрішніх вузлів помітно перевищує число зовнішніх вузлів.

Використовуючи суперелементи, можна провести розрахунок поетапно, істотно понизивши на кожному етапі розмірність завдання. Спочатку будують матрицю жорсткості для всіх типів суперелементів, потім розраховують систему, що складається з суперелементів. В результаті цього розрахунку визначають переміщення супервузлів. На заключному етапі розраховують кожен з суперелементів на задані переміщення супервузлів.

Використання суперелементів доцільне у таких випадках:

•  передбачувана розмірність задачі при скінченно-елементному розбитті перевершує можливості комп’ютера (пам’ять, швидкодія, погана обумовленість матриці);
•   у задачі міститься велика кількість ідентичних конструктивних елементів (панелі, об’ємні блоки і т.п.);
•   наявні типові конструктивні елементи, які вже були сформовані для об’єктів, що були розраховані раніше;
•   є локальне зосередження елементів, що нелінійно деформуються.

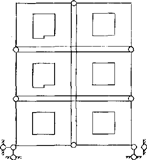
Бувають випадки, коли задача містить декілька різних об’єктів, що відрізняються матеріалами, набором скінченних елементів, геометрією і т.п. Наприклад, при розрахунку панельних будинків дрібне розбиття кожної панелі призводить до великої розмірності задачі, а застосування суперелементів дозволяє істотно знизити вплив розмірності подібних задач на швидкість їх виконання (рис. 5.2). При цьому варто врахувати й те, що кількість типів суперелементів у таких задачах, зазвичай, невелика.

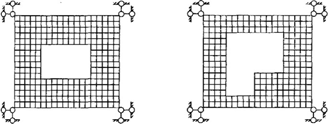а)   б)

Рисунок 5.2 – Діафрагма багатоповерхової будівлі (а) та відповідні їй типи

Істотного скорочення часу розрахунку можна досягти при розв’язуванні нелінійних задач, у яких наявні крупні включення, що лінійно деформуються. Наприклад, складні будівлі, що опираються на пружну основу. Для таких будівель врахування нелінійної роботи основи має істотне значення. У цьому випадку наземну будівлю необхідно оголосити суперелементом, матриця жорсткості якого на кожному кроці нелінійного розрахунку залишається незмінною.

Теоретично суперелементи у свою чергу можна розбивати на підсхеми (суперелементи 2-го рангу), розвиваючи цей процес і організовуючи своєрідну багаторангову рекурсію. У ПК ЛІРА реалізований лише один ранг суперелементів. У переважній більшості випадків цього достатньо для описання розрахункової схеми дуже високої розмірності.

Використання суперелементів корисне не лише для зменшення розмірності вирішуваного завдання, але і для зручності синтезу і аналізу.