Теоретичний матеріал до теми 1. Загальна рівновага і ефективність

Умови ефективності у виробництві розглянемо для економіки, де відомі фіксовані обсяги ресурсів, що використовуються у виробництві благ. У такій системі треба прийняти рішення про розподіл ресурсів між різними галузями, кожна з яких випускає одне благо, і визначити оптимальні обсяги виробництва благ.

Ефективність (оптимальність за Парето) у виробництві досягається при такому розподілі ресурсів між галузями, що неможливий їх перерозподіл, який збільшував би виробництво будь-якого блага без зменшення виробництва хоча б одного з інших благ.

Для геометричної інтерпретації проблеми розподілу ресурсів скористаємось графічною моделлю Еджворта для виробництва, яка зовні схожа на відповідну модель для економіки обміну.

Нехай для виробництва двох благ, X та У (кожне з яких випускає одна фірма) використовуються два види ресурсів у фіксованих обсягах — праця (L₀) і капітал (К₀), які розподіляються між двома виробничими процесами (тобто між двома фірмами) так, що виконуються балансові умови:

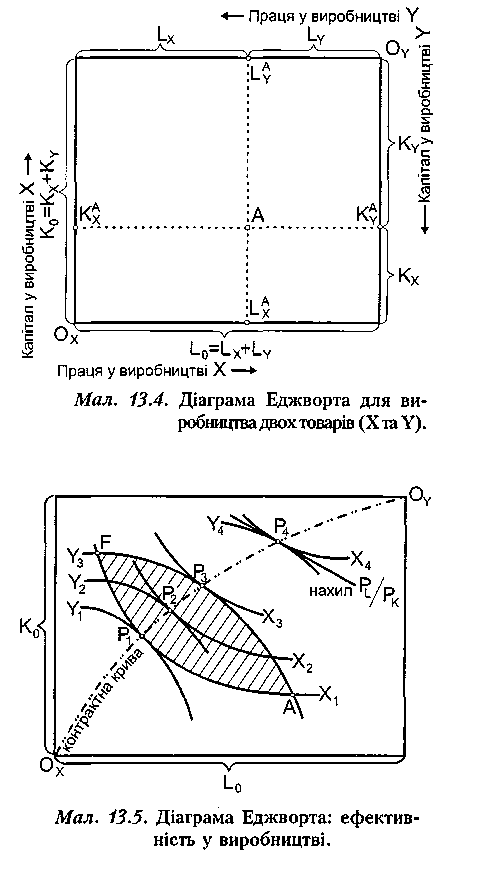
Графічно всі можливі варіанти розподілу двох обмежених ресурсів між двома фірмами можна показати на діаграмі (ящику) Еджворта для виробництва (мал. 13.4), на якій суміщаються дві системи координат — одна для виробника блага X (початок системи координат у нижньому лівому кутку — точка О_х), інша для виробника блага У (початок системи координат у правому верхньому кутку — точка О_Y). Довжина і висота ящика визначаються сукупними запасами ресурсів, згідно з умовою (13.5). Будь-яка точка на діаграмі буде мати чотири координати і відбиватиме варіант розподілу ресурсів між двома фірмами; наприклад, точці А на мал. 13.4 відповідає розподіл ресурсів між першою фірмою - (L_Х^А,К_Х^Л) і другою - ($L_Y^A$,$K_Y^A$).

Для кожної з фірм можна побудувати ізокванти, які відповідають певним обсягам випуску: для першої — Х₁, Х₂, Х₃ Х₄, для другої — У₄, У₃, У₂ У₁ (мал. 13.5); тут обсяги X та У перераховані в послідовності зростання випуску. Початковий розподіл ресурсів у точці А дає змогу фірмам забезпечити обсяги випуску Х₁ та У.₃.

Якщо порівняти стан А зі станом Р₁ (який досягається внаслідок певного перерозподілу ресурсів), то перша фірма не скорочує свій випуск Х₁ а друга збільшує випуск з У₃ до У_3. При іншому варіанті перерозподілу, що приводить до стану $P_3$, навпаки, друга фірма не змінює випуск, а перша підвищує свій з Х₁ до Х₃. Можливі також варіанти перерозподілу, коли обидві фірми збільшують свій випуск, наприклад, до рівнів Х₂ та У₂ (стан Р₂). Отже, всі варіанти перерозподілу ресурсів, які відповідають точкам заштрихованого сектора АР₁FР₃ (окрім точки F ), означають покращення за Парето.

. Як було вже визначено у темі 6, кожна окрема фірма використовує ефективну (оптимальну) комбінацію ресурсів, що мінімізує вартість виробництва, якщо виконується умова:

Але ринкові ціни факторів $P_L$ $P_K$ для кожної ситуації на ринку однакові для всіх фірм. Отже, якщо кожний виробник досягає ефективності у виробництві, то для граничних норм технологічного заміщення, МRТS^Х і МRТS^У, у виробництві, відповідно, благ X та У має виконуватись співвідношення

Це і є умовою ефективності (оптимальності за Парето) у виробництві, тому що при виконанні співвідношення (13.7) покращення за Парето за наявних запасів ресурсів неможливе. На мал. 13.5 показано точку Р₄, яка відповідає умові (13.7): в цій точці нахили ізоквант Х₄ та У₄ співпадають з нахилом Р_[ /Р_к спільної дотичної до цих двох ізоквант.

Умові (13.7) відповідають також точки Р₁ Р₂, Р₃ Якщо з’єднати ці точки плавною лінією, отримаємо контрактну криву для виробництва — множину ефективних варіантів розподілу ресурсів у діаграмі Еджворта, які є оптимальними

за Парето.

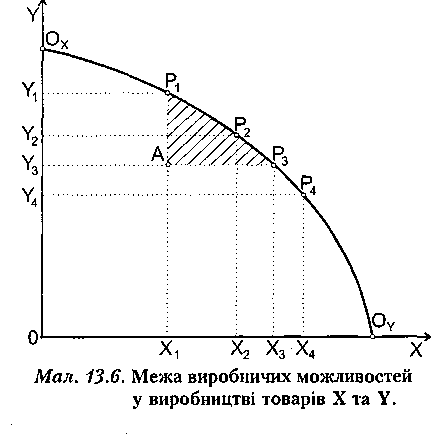
Кожній точці на контрактній кривій відповідають певні обсяги випуску для двох фірм. Отже, можна побудувати систему координат (мал. 13.6), де на осях відкладаються обсяги виробництва благ X та У. Для кожної точки діаграми Еджворта на мал. 13.5 (варіант розподілу ресурсів) є аналогічна точка на мал. 13.6 (обсяги готової продукції X, Y). Тоді контрактну криву можна трансформувати у лінію на новому малюнку - криву виробничих можливостей. (Слід звернути увагу на те, що точці О_х на мал. 13.6 відповідає ситуація, коли всі

ресурси використовуються для виробництва блага У, а Х=0; і навпаки, точці О_Y відповідають обсяги виробництва У=0, Х>0).

Крива (межа) виробничих можливостей, або крива трансформації (РРС) — лінія, яка показує максимально можливий обсяг випуску одного з благ для кожного даного обсягу випуску іншого блага при фіксованих запасах ресурсів в економіці та незмінних технологіях. При русі вздовж цієї кривої за рахунок перерозподілу ресурсів між різними виробництвами відбувається начебто трансформація одного блага в інше. Крива трансформації є графіком функції трансформації:

Всі точки кривої виробничих можливостей є оптимальними за Парето. Крива є межею, яка відокремлює досяжні обсяги випуску (точки самої кривої і внутрішні точки типу точки А) від недосяжних для економіки з фіксованими запасами ресурсів обсягів випуску. Для внутрішніх точок, на відміну від точок межі, умови ефективності у виробництві не діють, і тому є можливість збільшення випуску продукції за рахунок перерозподілу ресурсів (зверніть увагу, що точці А у наведеному прикладі відповідає повне використання наявних ресурсів, так само як і точкам межі виробничих можливостей, хоча максимально можливий випуск у точці А не забезпечується). На мал. 13.6 всі точки заштрихованого сектора АР₁Р₃ відповідають варіантам розподілу ресурсів, які ведуть до покращення за Парето у виробництві благ X та У порівняно із станом А. Рух у напрямку межі виробничих можливостей на мал. 13.6 (чи контрактної кривої на мал. 13.5) веде до покращення за Парето за тих умов, що всі фірми мінімізують вартість виробництва, а ринки є повністю конкурентними.

Крива виробничих можливостей демонструє альтернативну вартість виробництва різних благ. Адже, якщо ми вийшли на межу виробничих можливостей економіки при повному використанні ресурсів, подальше збільшення випуску кожного з благ можливе лише при скороченні випуску якогось з інших благ. Так, збільшення випуску блага X на величину $∆X=X_2-X_1$, яке відбувається при переході з точки Р₁ у Р₂ на мал. 13.6, вимагає скорочення випуску блага Y на величину $∆Y=Y_2-Y_1$ (за абсолютною величиною). Тому альтернативна вартість додаткового випуску $∆$Х дорівнює DY.

Нахил кривої виробничих можливостей дорівнює граничній нормі трансформації (МRТ), яка показує, від виробництва скількох одиниць блага Y треба відмовитись для збільшення виробництва блага X на одиницю (за даних обсягів ресурсів та незмінних технологіях):

(знак мінус виникає тому, що МRТ, за визначенням, є величиною додатною). З урахуванням того, що $∆X$ і $∆Y$ вимірюються в одиницях альтернативної вартості, а альтернативна вартість випуску додаткової одиниці продукції Y є граничною вартістю МС_Х виробництва продукції X, і навпаки, маємо, що

МКТ зростає в міру збільшення випуску блага X, що ілюструє зростаючу альтернативну вартість при збільшенні випуску блага X, адже в міру скорочення випуску одного блага і збільшення іншого стає все важчим переміщувати ресурси із галузі в галузь. До того ж залучення для виробництва блага X все нових обсягів ресурсів, які використовувались у виробництві блага Y, стає дедалі менш ефективним. Тут вступає в дію закон спадної граничної віддачі факторів виробництва, що призводить до зростання вартості виробництва кожної додаткової одиниці блага. У зв’язку із зростанням альтернативної вартості, при русі вздовж кривої трансформації вона є опуклою в бік від початку координат.